Giải PT: 5+8:(x2-4)=(2x-1):(x+2)-(3x-1):(2-x)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Spam Spam SpamSpam SpamSpamSpamSpamSpamSpamSpamSpamSpamSpamSpamSpamSpamSpamSpamSpamSpamSpamSpamSpamSpamSpamSpamSpamSpamSpamSpam
SpamSpamSpamSpamSpamSpamSpamSpamSpam


a) Xét \(\Delta ABM\)có: \(AM//DE\)(giả thiết).
\(\Rightarrow\frac{BD}{BM}=\frac{DE}{AM}\)(hệ quả của định lí Ta-lét)..
\(\Rightarrow BD.AM=DE.BM\)(điều phải chứng minh).

à thanks mình xin lỗi nhé !
a, Xét tam giác HAC và tam giác ABC ta có
^AHC = ^BAC = 900
^C _ chung
Vậy tam giác HAC ~ tam giác ABC ( g.g ) (1)
\(\Rightarrow\frac{HA}{AB}=\frac{AC}{BC}\) ( tí số đồng dạng ) (3)
Xét tam giác HAB và tam giác ABC ta có :
^AHB = ^BAC = 900
^B _ chung
Vậy tam giác HAB ~ tam giác ABC ( g.g ) (2)
Từ (1) ; (2) suy ra : tam giác HAC ~ tam giác HAB
b, Từ (3) ta có : \(\frac{HA}{15}=\frac{20}{25}\)( BC = 25 cm theo Py ta go )
\(\Rightarrow HA=\frac{15.20}{25}=12\)cm

Nhận thấy (2020 - x) + (2021 - x) + (2x - 4041) = 0
Khi đó : (2020 - x)3 + (2021 - x)3 + (2x - 4041)3 = 0
<=> 3(2020 - x)(2021 - x)(2x - 4041) = 0
<=> (2020 - x)(2021 - x)(2x - 4041) = 0
<=> 2020 - x = 0 hoặc 2021 - x = 0 hoặc 2x - 4041 = 0
<=> x = 2020 hoặc x = 2021 hoặc x = 4041/2
Vậy \(x\in\left\{2020;2021;-\frac{4041}{2}\right\}\)là nghiệm phương trình

x(4x-1)2(2x-1)=9
=> (4x-1)2 [ x( 2x - 1 ) = 9
=>(16x2 - 8x +1 ) (2x2 - x ) = 9
=>(16x2 - 8x +1 ) 8(2x2 - x ) = 9.8
=>(16x2 - 8x +1 ) (16x2 - 8x ) = 72
Đặt 16x2 - 8x = y ( y > -1)
Thay y vào ta có:
(y + 1)y = 72
=> y2 + y - 72 =0
=>y2 + 9y - 8y - 72 = 0
=>(y2 + 9y) - (8y + 72) = 0
=>(y + 9 ) (y - 8) =0
=> [
<=> x = 0 hoặc x = 1/2 Vậy tập nghiệm của phương trình la S = {0 ; 1/2 }
12
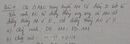
\(5+\frac{8}{x^2-4}=\frac{2x-1}{x+2}-\frac{3x-1}{2-x}\left(ĐKXĐ:x\ne\pm2\right)\)
\(\Leftrightarrow5+\frac{8}{\left(x-2\right)\left(x+2\right)}=\frac{2x-1}{x+2}+\frac{3x-1}{x-2}\)
\(\Leftrightarrow\frac{5\left(x-2\right)\left(x+2\right)}{\left(x-2\right)\left(x+2\right)}+\frac{8}{\left(x-2\right)\left(x+2\right)}\)\(=\frac{\left(2x-1\right)\left(x-2\right)}{\left(x+2\right)\left(x-2\right)}+\frac{\left(3x-1\right)\left(x+2\right)}{\left(x+2\right)\left(x-2\right)}\)
\(\Rightarrow5\left(x-2\right)\left(x+2\right)+8=\)\(\left(2x-1\right)\left(x-2\right)+\left(3x-1\right)\left(x+2\right)\)
\(\Leftrightarrow5\left(x^2-4\right)+8=2x^2-4x-x+2\)\(+3x^2+6x-x-2\)
\(\Leftrightarrow5x^2-20+8=\)\(5x^2\)
\(\Leftrightarrow-12=5x^2-5x^2\)
\(\Leftrightarrow0=-12\)(vô nghiệm).
Vậy phương trình đã cho vô nghiệm.