cho tam giácabc có ab=ac m là trung điểm của bc n là trung điểm của ab trên tie đối nc lấy k sao cho nc=nk trên tia am lấy p sao cho mp=ma chứng minh bs=a điểm kpb thẳng hàng
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Lời giải:
$(x+7)^{n+1}-(x+7)^{n-3}=0$
$(x+7)^{n-3}[(x+7)^4-1]=0$
$\Rightarrow (x+7)^{n-3}=0$ hoặc $(x+7)^4-1=0$
Nếu $(x+7)^{n-3}=0$
$\Rightarrow x+7=0\Rightarrow x=-7$
Nếu $(x+7)^4-1=0$
$\Rightarrow (x+7)^4=1=1^4=(-1)^4$
$\Rightarrow x+7=1$ hoặc $x+7=-1$
$\Rightarrow x=-6$ hoặc $x=-8$.

Lời giải:
Áp dụng BĐT dạng $|a|+|b|\geq |a+b|$ ta có:
$|x-2011|+|2025-x|\geq |x-2011+2025-x|=4$
$|x-2023|\geq 0$ với mọi $x$
$\Rightarrow P=|x-2011|+|2025-x|+|x-2023|\geq 4+0=4$
Vậy $P_{\min}=4$
Giá trị này đạt tại $(x-2011)(2025-x)\geq 0$ và $x-2023=0$
Hay $x=2023$.

a: Xét ΔBAD và ΔBED có
BA=BE
\(\widehat{ABD}=\widehat{EBD}\)
BD chung
Do đó: ΔBAD=ΔBED
b: Ta có: ΔBAD=ΔBED
=>DA=DE
=>D nằm trên đường trung trực của AE(1)
Ta có: BA=BE
=>B nằm trên đường trung trực của AE(2)
Từ (1),(2) suy ra BD là đường trung trực của AE
c: ΔBAD=ΔBED
=>\(\widehat{BAD}=\widehat{BED}\)
=>\(\widehat{BED}=90^0\)
=>DE\(\perp\)BC
Gọi H là giao điểm của AB và CK
Xét ΔBHC có
BK,CA là các đường cao
BK cắt CA tại D
Do đó: D là trực tâm của ΔBHC
=>DH\(\perp\)BC
mà DE\(\perp\)BC
và DH,DE có điểm chung là D
nên H,D,E thẳng hàng
=>BA,DE,CK đồng quy

a: ΔABC cân tại A
=>\(\widehat{ABC}=\widehat{ACB}\)
=>\(\widehat{ACB}=47^0\)
ΔABC cân tại A
=>\(\widehat{BAC}=180^0-2\cdot\widehat{ABC}=180^0-2\cdot47^0=86^0\)
b: Xét ΔAMB và ΔAMC có
AM chung
MB=MC
AB=AC
Do đó: ΔAMB=ΔAMC
c Xét ΔAMB có AM+BM>AB
mà AB=AC(ΔABC cân tại A)
nên AM+BM>AC
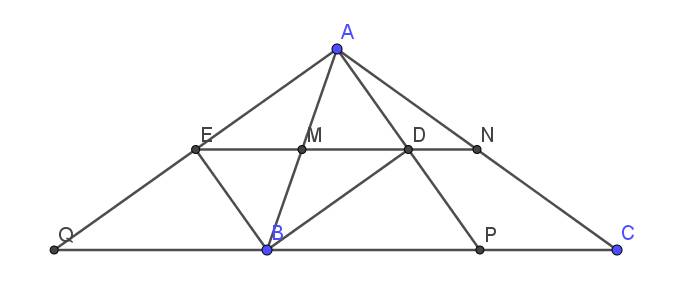

Xét ΔNBK và ΔNAC có
NB=NA
\(\widehat{BNK}=\widehat{ANC}\)(hai góc đối đỉnh)
NK=NC
Do đó: ΔNBK=ΔNAC
=>\(\widehat{NBK}=\widehat{NAC}\)
mà hai góc này là hai góc ở vị trí so le trong
nên KB//AC
Xét ΔMBP và ΔMCA có
MB=MC
\(\widehat{BMP}=\widehat{CMA}\)
MP=MA
Do đó: ΔMBP=ΔMCA
=>\(\widehat{MBP}=\widehat{MCA}\)
mà hai góc này là hai góc ở vị trí so le trong
nên BP//AC
ta có: BP//AC
BK//AC
BP,BK có điểm chung là B
Do đó: P,B,K thẳng hàng
Xét tam giác ABC có AB = AC và M là trung điểm của cạnh BC. Gọi N là trung điểm của cạnh AB.
Ta có:
AB = AC (do tam giác ABC cân tại đỉnh A).
BM = CM (vì M là trung điểm của BC).
AM cạnh chung.
Suy ra: ΔAMB = ΔAMC (c.c.c) ⇒ ∠AMB = ∠AMC (hai góc tương ứng).
Ta còn biết:
∠AMB + ∠AMC = 180° (hai góc kề bù).
∠AMB = ∠AMC = 90°.
Vậy AM vuông góc với BC.
Chứng minh rằng điểm KPB thẳng hàng không được yêu cầu trong đề bài, nhưng ta có thể tiếp tục xem xét tam giác ABC để tìm các thông tin khác nếu bạn muốn.