

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Số đoạn thẳng vẽ được là:
\(24\times\dfrac{\left(24-1\right)}{2}=12\times23=276\left(đoạn\right)\)

a: ĐKXĐ: \(x\ne\dfrac{1}{2}\)
Để \(\dfrac{5x}{2x-1}\) là số hữu tỉ thì \(2x-1\ne0\)
=>\(x\ne\dfrac{1}{2}\)
b: ĐKXĐ: x<>-1
Để \(\dfrac{x+5}{2x+2}\) là số nguyên thì \(x+5⋮2x+2\)
=>\(2x+10⋮2x+2\)
=>\(2x+2+8⋮2x+2\)
=>\(8⋮2x+2\)
mà 2x+2 chẵn
nên \(2x+2\in\left\{2;-2;4;-4;8;-8\right\}\)
=>\(x\in\left\{0;-2;1;-3;3;-5\right\}\)
c: ĐKXĐ: x<>-2
Để \(\dfrac{x^2+2x+3}{x+2}\) là số nguyên thì \(x^2+2x+3⋮x+2\)
=>\(x\left(x+2\right)+3⋮x+2\)
=>\(3⋮x+2\)
=>\(x+2\in\left\{1;-1;3;-3\right\}\)
=>\(x\in\left\{-1;-3;1;-5\right\}\)

Giải
Dấu chấm hỏi là 109 nha bạn vì
Ở tam giác 1 ta có
1 mũ 2 + 2 mũ 2 + 3 mũ 2 = 14
Tam giác 2
4 mũ 2 + 5 mũ 2 + 7 mũ 2 = 90
Tam giác 4
4 mũ 2 + 7 mũ 2 + 10 mũ 2 = 165
Từ đó ta có tam giác 3
3 mũ 2 +6 mũ 2 +8 mũ 2 = 109

Các tập con của {1; 2; 3; 4; 5} là:
∅; {1}; {2}; {3}; {4}; {5};
{1; 2}; {1; 3}; {1; 4}; {1; 5};
{2; 3}; {2; 4}; {2; 5}
{3; 4}; {3; 5}; {4; 5};
{1; 2; 3}; {1; 2; 4}; {1; 2; 5};
{2; 3; 4}; {2; 3; 5}; {3; 4; 5};
{1; 2; 3; 4}; {1; 2; 3; 5}; {2; 3; 4; 5};
{1; 2; 3; 4; 5}
Các tập con của {1; 2; 3; 4; 5} là:
\(\varnothing\); {1}; {2}; {3}; {4}; {5}; {1; 2}; {1; 3}; {1; 4}; {1; 5}; {2; 3}; {2; 4}; {2; 5};
{3; 4}; {3; 5}; {4; 5}; {1; 2; 3}; {1; 2; 4}; {1; 2; 5}; {1; 3; 4}; {1; 3; 5}; {1; 4; 5}
{2; 3; 4}; {2; 3; 5}; {2; 4; 5}; {3; 4; 5}; {1; 2; 3; 4}; {1; 2; 3; 5}; {1; 2; 4; 5}
{1; 3; 4; 5}; {2; 3; 4; 5}; {1; 2; 3; 4; 5}

Lời giải:
\(P^2=\frac{1.3}{2^2}.\frac{3.5}{4^2}.\frac{5.7}{6^2}...\frac{397.399}{398^2}.\frac{1.399}{400^2}\)
Xét thừa số tổng quát $\frac{n(n+2)}{(n+1)^2}=\frac{n^2+2n}{n^2+2n+1}<1$ với mọi $n$ tự nhiên.
$\Rightarrow \frac{1.3}{2^2}< 1; \frac{3.5}{4^2}<1;...; \frac{397.399}{398^2}<1$
$\Rightarrow P^2< 1.1....1.\frac{1.399}{400^2}=\frac{399}{400^2}< \frac{1}{400}$
$\Rightarrow P< \frac{1}{20}$

tk ạ!
Ta có:
p20 - 1=(p4 - 1)(p16 + p12 + p8 + p4 + 1)
Do p là số nguyên tố lớn hơn 5⇒ p là 1 số lẻ
p2 + 1 và p2 - 1 là các số chẵn
p4 - 1 ⋮ 4
p20 - 1 ⇒4
vì p là số nguyên tố lớn hơn 5⇒ p là số không chia hết cho 5
p4 - 1 ⋮ 5
lập luận được p16 + p12 + P8 + p4 + 1 ⋮ 5
⇒ p20 - 1 chia hết cho 25
Mà (4;25) = 1
Nên 𝑝20p
20- 1 chia hết cho 100

Bài 2:
\(x^2-xy-y+2=0\)
=>\(x^2-1+3-y\left(x+1\right)=0\)
=>\(\left(x-1\right)\left(x+1\right)-y\left(x+1\right)=-3\)
=>(x+1)(x-1-y)=-3
=>\(\left(x+1;x-1-y\right)\in\left\{\left(1;-3\right);\left(3;-1\right);\left(-1;3\right);\left(-3;1\right)\right\}\)
TH1: \(\left\{{}\begin{matrix}x+1=1\\x-1-y=-3\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=0\\y=x-1-\left(-3\right)=x-1+3=x+2=0+2=2\end{matrix}\right.\)
TH2: \(\left\{{}\begin{matrix}x+1=3\\x-1-y=-1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=2\\y=x-1+1=x=2\end{matrix}\right.\)
TH3: \(\left\{{}\begin{matrix}x+1=-1\\x-1-y=3\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=-2\\y=x-1-3=x-4=-2-4=-6\end{matrix}\right.\)
TH4: \(\left\{{}\begin{matrix}x+1=-3\\x-1-y=1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=-4\\y=x-1-1=x-2=-4-2=-6\end{matrix}\right.\)

Câu 6
Chu vi thửa ruộng:
AB + BC + CD + DE + EF + FG + GH + HA
= (15 - 4) : 2 + 3 + 2 + 3 + (15 - 4) : 2 + 8 + 15 + 8
= 50 (m)
Diện tích hình chữ nhật AFDH:
8 . 15 = 120 (m²)
Diện tích hình thang cân BCDE:
(4 + 2) . 4 : 2 = 12 (m²)
Diện tích thửa ruộng:
120 - 12 = 108 (m²)
Số kg thóc thu được:
108 × 0,5 = 54 (kg)
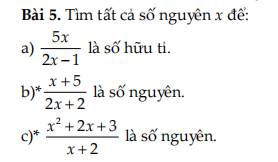



Câu 1: B
Câu 2: A
Câu 3: B
Câu 4: C
Câu 5: D
Câu 6: A
Câu 7: \(\dfrac{x+2}{6}=\dfrac{-15}{2}\)
=>\(\dfrac{x+2}{6}=\dfrac{-45}{6}\)
=>x+2=-45
=>x=-47
=>Chọn C
Câu 8: B
Câu 9: C
Câu 10: A
Câu 11: \(x\cdot\dfrac{3}{4}=\dfrac{7}{8}\)
=>\(x=\dfrac{7}{8}:\dfrac{3}{4}=\dfrac{7}{8}\cdot\dfrac{4}{3}=\dfrac{28}{24}=\dfrac{7}{6}\)
=>Chọn C
Câu 12: C
Câu 13: D
Câu 14; C
Câu 15: A
Câu 16: D
II: Tự luận:
Bài 2:
a: \(3\dfrac{1}{3}x+16=13,25\)
=>\(x\cdot\dfrac{10}{3}=13,25-16=-2,75\)
=>\(x=-\dfrac{11}{4}:\dfrac{10}{3}=-\dfrac{11}{4}\cdot\dfrac{3}{10}=\dfrac{-33}{40}\)
b: \(x-43=\left(57-x\right)-50\)
=>x-43=7-x
=>2x=50
=>x=25
Các bn ơi,giúp mk với mk đag cần gấp lắm!!!!