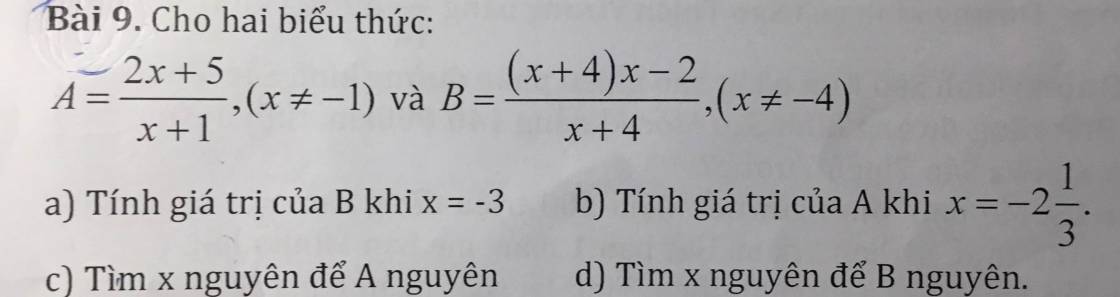
giúp ý c và d còn a và b thì không cần
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(a,B=\dfrac{\left(-3+4\right).\left(-3\right)-2}{-3+4}=\dfrac{-3-2}{1}=-5\\ d,A=\dfrac{2.\left(-2\dfrac{1}{3}\right)+5}{-2\dfrac{1}{3}+1}=\dfrac{2.\dfrac{-7}{3}+5}{-\dfrac{7}{3}+1}=\dfrac{-\dfrac{14}{3}+5}{-\dfrac{4}{3}}=\dfrac{\dfrac{1}{3}}{-\dfrac{4}{3}}=-\dfrac{1}{4}\)

a) Ta có:
- Gọi M là trung điểm của AC.
- Vì I là trung điểm của BC nên IM // AH (vì I và H đều là trung điểm của các cạnh của tam giác ABC).
- Ta có BM = MC (vì M là trung điểm của AC).
- Vì IM // AH và BM = MC nên tam giác IMC và tam giác AHM là hai tam giác đồng dạng.
- Do đó, ta có: ∠IMC = ∠AHM.
- Nhưng ∠IMC = 90° (vì IM vuông góc với BC).
- Vậy, ta có: ∠AHM = 90°.
- Từ đó, ta suy ra AH vuông góc với BC.
b) Ta có:
- Gọi K là điểm đối xứng của H qua I.
- Vì I là trung điểm của BC nên IK // AH (vì I và H đều là trung điểm của các cạnh của tam giác ABC).
- Vì K là điểm đối xứng của H qua I nên HK = HI.
- Ta có: AH = 2IK (vì I là trung điểm của BC và K là điểm đối xứng của H qua I).
- Vì CK // BD (vì CK và BD đều vuông góc với BC và đi qua điểm H) nên tam giác CKD và tam giác BHD là hai tam giác đồng dạng.
- Do đó, ta có: CK/BD = DK/DH.
- Nhưng CK = BD (vì CK // BD) nên DK = DH.
- Vậy, ta có: DK = DH.
- Từ đó, ta suy ra tam giác ABK vuông.
c) Ta có:
- Gọi N là trung điểm của AB.
- Vì I là trung điểm của BC nên IN // AH (vì I và H đều là trung điểm của các cạnh của tam giác ABC).
- Ta có: AN = NB (vì N là trung điểm của AB).
- Vì IN // AH và AN = NB nên tam giác INB và tam giác AHM là hai tam giác đồng dạng.
- Do đó, ta có: ∠INB = ∠AHM.
- Nhưng ∠INB = 90° (vì IN vuông góc với AB).
- Vậy, ta có: ∠AHM = 90°.
- Từ đó, ta suy ra AH vuông góc với BM.
- Nhưng BM = MC (vì M là trung điểm của AC).
- Vậy, ta có: AH vuông góc với MC.
- Từ đó, ta suy ra tam giác BEA vuông.
d) Ta có:
- Gọi N là trung điểm của AB.
- Vì I là trung điểm của BC nên IN // AH (vì I và H đều là trung điểm của các cạnh của tam giác ABC).
- Ta có: AN = NB (vì N là trung điểm của AB).
- Vì IN // AH và AN = NB nên tam giác INB và tam giác AHM là hai tam giác đồng dạng.
- Do đó, ta có: ∠INB = ∠AHM.
- Nhưng ∠INB = 90° (vì IN vuông góc với AB).
- Vậy, ta có: ∠AHM = 90°.
- Từ đó, ta suy ra AH vuông góc với BM.
- Nhưng BM = MC (vì M là trung điểm của AC).
- Vậy, ta có: AH vuông góc với MC.
- Gọi D' là điểm đối xứng của D qua M.
- Ta có: MD' = MD (vì D' là điểm đối xứng của D qua M).
- Vì MD' vuông góc với BC và MD vuông góc với BC nên tam giác MBD' và tam giác MCD là hai tam giác vuông cân.
- Do đó, ta có: MB = MD' và MC = MD.
- Từ đó, ta suy ra MB.MC = MD.MD' = MD^2.
- Nhưng MD^2 = DC^2 - MC^2 (theo định lí Pythagoras).
- Vậy, ta có: MB.MC = DC^2 - MC^2.

Có VT = \(\sqrt{\dfrac{1}{x^2}+\dfrac{1}{y^2}+\dfrac{1}{z^2}}=\sqrt{\left(\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}\right)^2-\dfrac{2}{xy}-\dfrac{2}{yz}-\dfrac{2}{zx}}\)
\(=\sqrt{\left(\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}\right)^2-\dfrac{2}{xyz}\left(x+y+z\right)}\)
\(=\sqrt{\left(\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}\right)^2}=\left|\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}\right|=VP\) (Vì x + y + z = 0)

a) Hệ phương trình có nghiệm duy nhất là
\(\left\{{}\begin{matrix}2x-y=3\\x+4y=6\end{matrix}\right.\)
b) Hệ phương trình có vô số nghiệm là
\(\left\{{}\begin{matrix}2x-y=3\\4x-2y=6\end{matrix}\right.\)

\(\dfrac{\sqrt{15}-\sqrt{5}}{\sqrt{3}-1}+\dfrac{5-2\sqrt{5}}{2\sqrt{5}-4}\)
\(=\dfrac{\sqrt{5}\left(\sqrt{3}-1\right)}{\sqrt{3}-1}+\dfrac{\sqrt{5}\left(\sqrt{5}-2\right)}{2\left(\sqrt{5}-2\right)}\)
\(=\sqrt{5}+\dfrac{\sqrt{5}}{2}\)
\(=\dfrac{2\sqrt{5}+\sqrt{5}}{2}\)
\(=\dfrac{3\sqrt{5}}{2}\)

1/
Ta có
sđ cung AC = sđ cung BC (1)
\(sđ\widehat{CFG}=\dfrac{1}{2}\left(sđcungBC+sđcungAE\right)\) (góc có đỉnh ở trong hình tròn) (2)
\(sđ\widehat{CHE}=\dfrac{1}{2}sđcungCAE=\dfrac{1}{2}\left(sđcungAC+sđcungAE\right)\) (góc nội tiếp) (3)
Từ (1) (2) (3) \(\Rightarrow\widehat{CFG}=\widehat{CHE}\)
Ta có
\(\widehat{CFG}+\widehat{EFG}=\widehat{EFC}=180^o\)
\(\Rightarrow\widehat{CHE}+\widehat{EFG}=180^o\)
=> EFGH là tứ giác nội tiếp (Tứ giác có hai góc đối bù nhau là tứ giác nội tiếp)
2/
sđ cung AC = sđ cung BC (4)
\(sđ\widehat{AGC}=\dfrac{1}{2}\left(sđcungAC+sđcungBH\right)\) (5) (góc có đỉnh ở trong hình tròn)
\(sđ\widehat{CHy}=\dfrac{1}{2}sđcungCBH=\dfrac{1}{2}\left(sđcungBC+sđcungBH\right)\) (6) (Góc giữa tiếp tuyến và dây cung)
Từ (4) (5) (6) \(\Rightarrow\widehat{AGC}=\widehat{CHy}\)
Mà AC = AG (gt) => tgACG cân tại A \(\Rightarrow\widehat{AGC}=\widehat{ACG}\)
\(\Rightarrow\widehat{ACG}=\widehat{CHy}\) mà 2 góc trên ở vị trí so le trong => xy//AC

\(\sqrt[]{3-\sqrt[]{5}}:\sqrt[]{2}\)
\(=\sqrt[]{3-\sqrt[]{5}}.\dfrac{1}{\sqrt[]{2}}\)
\(=\dfrac{\sqrt[]{3-\sqrt[]{5}}}{\sqrt[]{2}}\)
\(=\sqrt[]{\dfrac{3-\sqrt[]{5}}{2}}\)
c, A = \(\dfrac{2x+5}{x+1}\) (\(x\ne\) -1)
A \(\in\) Z ⇔ 2\(x\) + 5 ⋮ \(x\) + 1
2(\(x+1\)) + 3 ⋮ \(x\) + 1
3 ⋮ \(x\) + 1
\(x+1\) \(\in\)Ư(3) = { -3; -1; 1; 3}
\(x\) + 1 \(\in\) { -4; -2; 0; 2}
d, B = \(\dfrac{\left(x+4\right)x-2}{\left(x+4\right)}\) (\(x\ne\) -4)
B \(\in\) Z ⇔ (\(x+4\))\(x\) - 2 ⋮ \(x+4\)
2 ⋮ \(x+4\)
\(x+4\) \(\in\) Ư(2) = { -2; -1; 1; 2}
\(x\) \(\in\) { -6; -5; -3; -2}