Cho e hỏi câu này ạ:
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(2P=6ab+2c\left(a+b\right)\)
\(2P=3\left(a^2+b^2+c^2\right)+6ab+2c\left(a+b\right)-3\left(a^2+b^2+c^2\right)\)
\(2P=3\left(a+b\right)^2+2c\left(a+b\right)+3c^2-3\left(a^2+b^2+c^2\right)\)
\(2P=\left(a+b+c\right)^2+2\left(a+b\right)^2+2c^2-3\left(a^2+b^2+c^2\right)\)
\(2P\ge-3\left(a^2+b^2+c^2\right)\ge-54\)
\(\Rightarrow P\ge-27\)
\(P_{min}=-27\) khi \(\left\{{}\begin{matrix}a^2+b^2+c^2=18\\a+b+c=0\\a+b=0\\c=0\end{matrix}\right.\) \(\Rightarrow\left(a;b;c\right)=\left(-3;3;0\right);\left(3;-3;0\right)\)

Tỉ số vải của cuộn A và cuộn B là:
`1/5:1/2=2/5`
Hiệu số phần bằng nhau là:
`5-2=3` (phần)
Số vải ở cuộn A là:
`12:3 xx 2=8(m)`
Số vải ở cuộn B là:
`12+8=20(m)`
ĐS: ...
1. Cuộn A có ít hơn cuộn B 12 mét:
\[
x = y - 12
\]
2. Một nửa số vải cuộn A bằng một phần năm số vải cuộn B:
\[
\frac{1}{2}x = \frac{1}{5}y
\]
\[
\frac{1}{2}x = \frac{1}{5}y
\]
\[
10 \times \frac{1}{2}x = 10 \times \frac{1}{5}y
\]
\[
5x = 2y
\]
\[
5(y - 12) = 2y
\]
\[
5y - 60 = 2y
\]
\[
5y - 2y = 60
\]
\[
3y = 60
\]
\[
y = 20
\]
Thay \( y = 20 \) vào phương trình \( x = y - 12 \):
\[
x = 20 - 12
\]
\[
x = 8
\]
Kết quả là cuộn A có 8 mét vải và cuộn B có 20 mét vải.

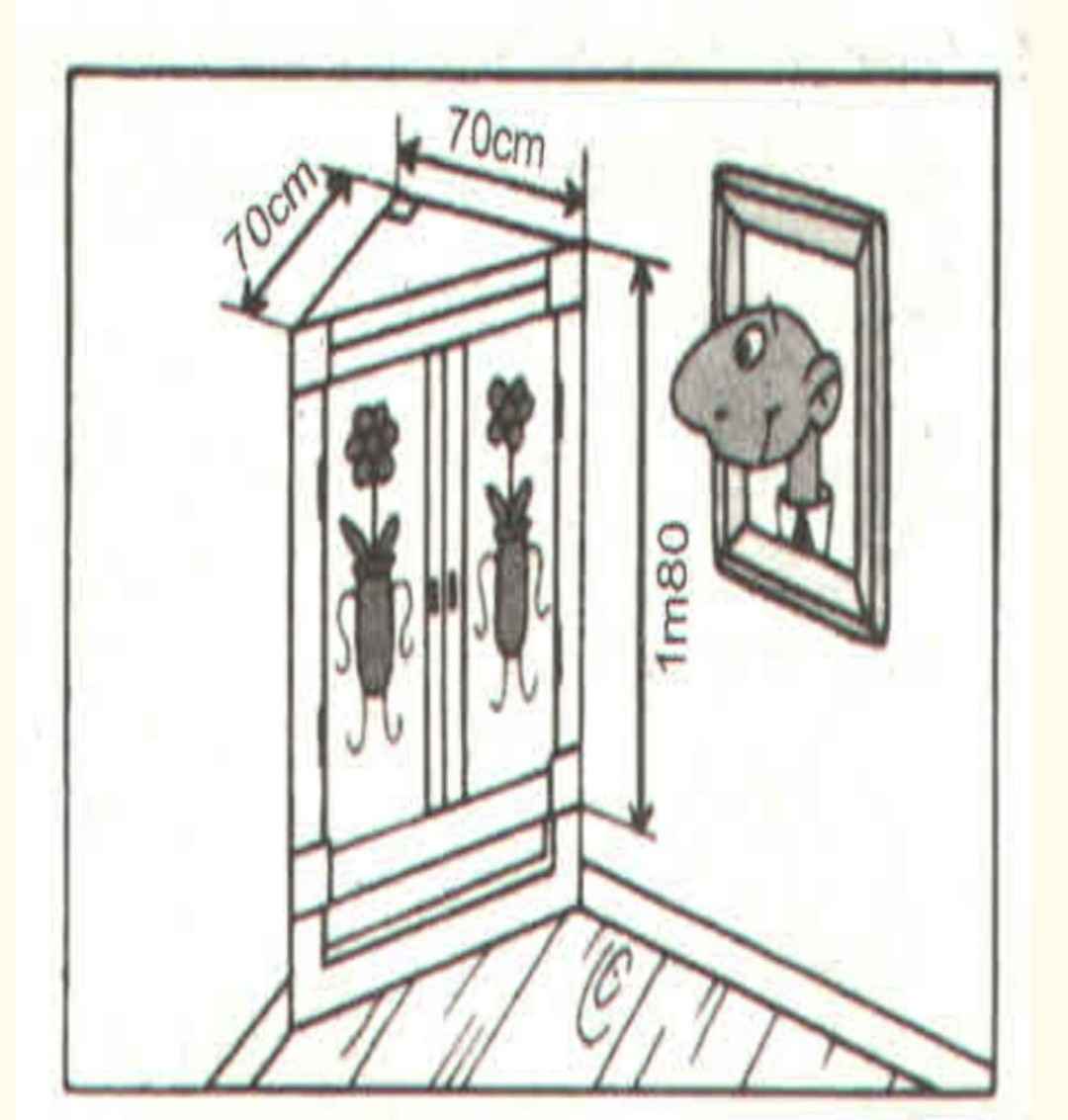
Độ dài cạnh đáy thứ ba của cái tủ là:
\(\sqrt{70^2+70^2}=70\sqrt{2}\left(cm\right)\)
Chu vi đáy của cái tủ là:
\(70+70+70\sqrt{2}=140+70\sqrt{2}\left(cm\right)\)
Diện tích xung quanh của của tủ là:
\(180\cdot\left(140+70\sqrt{2}\right)=25200+12600\sqrt{2}\left(cm^2\right)\)
Diện tích đáy của cái tủ là:
\(\dfrac{1}{2}\cdot70\cdot70=2450\left(cm^2\right)\)
Diện tích toàn phần của cái tủ là:
\(2\cdot2450+\left(25200+12600\sqrt{2}\right)=30100+12600\sqrt{2}\left(cm^2\right)\)

2)
\(a,8,2\times3,5+115+3,5\times1,8\\ =\left(8,2\times3,5+3,5\times1,8\right)+115\\ =3,5\times\left(8,2+1,8\right)+115\\ =3,5\times10+115\\ =35+115\\ =150\\ b,0,125\times0,12\times25\times1,7\times8\\ =\left(0,125\times8\right)\times\left(0,12\times25\right)\times1,7\\ =1\times3\times1,7\\ =3\times1,7\\ =5,1\)
Bài 1:
a: \(\left(57,17+8,63\right)\times9,5-98,44:2,3\)
=65,8x9,5-42,8
=625,1-42,8=582,3
b: \(61,35-8,6\times7,2:4,8+52,45\)
=61,35+52,45-12,9
=113,8-12,9=100,9

\(P=\dfrac{-\left(x^2+1\right)+2x^2-8x+8}{x^2+1}=-1+\dfrac{2\left(x-2\right)^2}{x^2+1}\ge-1\)
\(P_{min}=-1\) khi \(x-2=0\Rightarrow x=2\)
\(P=\dfrac{9\left(x^2+1\right)-8x^2-8x-2}{x^2+1}=9-\dfrac{2\left(2x+1\right)^2}{x^2+1}\le9\)
\(P_{max}=9\) khi \(2x+1=0\Rightarrow x=-\dfrac{1}{2}\)
\[
P = \frac{x^2 - 8x + 7}{x^2 + 1}
\]
\[
x^2 - 8x + 7 = (x^2 - 8x + 16) - 9 = (x-4)^2 - 9
\]
\[
P = \frac{(x-4)^2 - 9}{x^2 + 1}
\]
- Tại \( x = 0 \):
\[
P(0) = \frac{0^2 - 8 \times 0 + 7}{0^2 + 1} = \frac{7}{1} = 7
\]
- Tại \( x = 1 \):
\[
P(1) = \frac{1^2 - 8 \times 1 + 7}{1^2 + 1} = \frac{1 - 8 + 7}{2} = \frac{0}{2} = 0
\]
- Tại \( x = 2 \):
\[
P(2) = \frac{2^2 - 8 \times 2 + 7}{2^2 + 1} = \frac{4 - 16 + 7}{4 + 1} = \frac{-5}{5} = -1
\]
- Tại \( x = 4 \)
\[
P(4) = \frac{4^2 - 8 \times 4 + 7}{4^2 + 1} = \frac{16 - 32 + 7}{16 + 1} = \frac{-9}{17}
\]
- Tại \( x = -1 \):
\[
P(-1) = \frac{(-1)^2 - 8 \times (-1) + 7}{(-1)^2 + 1} = \frac{1 + 8 + 7}{1 + 1} = \frac{16}{2} = 8
\]
Dựa trên các giá trị đã tính, ta thấy rằng giá trị lớn nhất của \( P \) là \( 8 \) và giá trị nhỏ nhất là \( -1 \).
=> Max = 8
Min = -1

\(E=x^2-2xy+3y^2-2x-10y+20\\
=\left(x^2+y^2+1-2xy-2x+2y\right)+\left(2y^2-12y+72\right)-53\\
=\left(-x+y+1\right)^2+2\left(y-6\right)^2-53\)
Ta có:
`(-x+y+1)^2>=0` với mọi x,y
`2(y-6)^2>=0` với mọi y
`=>E=(-x+y+1)^2+2(y-6)^2-53>=-53` với mọi x,y
Dấu "=" xảy ra: `-x+y+1=0` và `y-6=0`
`<=>-x+7=0` và `y=6`
`<=>x=7` và `y=6`

\(D=\left(x^2-2xy+y^2\right)-12\left(x-y\right)+36+5y^2+9\)
\(=\left(x-y\right)^2-12\left(x-y\right)+36+5y^2+9\)
\(=\left(x-y-6\right)^2+5y^2+9\)
Do \(\left\{{}\begin{matrix}\left(x-y-6\right)^2\ge0\\5y^2\ge0\end{matrix}\right.\) ;\(\forall x;y\)
\(\Rightarrow D\ge9\)
\(D_{min}=9\) khi \(\left\{{}\begin{matrix}x-y-6=0\\5y^2=0\end{matrix}\right.\) \(\Rightarrow\left(x;y\right)=\left(6;0\right)\)

Ta có:
`14a + 21b + 5a - 2b`
`= (14a + 5a)+(21b - 2b)`
`= 19a + 19b`
`= 19. (a + b)`
`= 19 . 100`
`= 1900`
Vậy: `14a + 21b + 5a - 2b = 1900` với `a+b=100`

a: Xét ΔAHD vuông tại H và ΔDCB vuông tại C có
\(\widehat{ADH}=\widehat{DBC}\)(hai góc so le trong, AD//BC)
Do đó: ΔAHD~ΔDCB
b: Xét ΔBHA vuông tại H và ΔBAD vuông tại A có
\(\widehat{HBA}\) chung
DO đó ΔBHA~ΔBAD
=>\(\dfrac{BH}{BA}=\dfrac{BA}{BD}\)
=>\(BH\cdot BD=BA^2\)
c: ΔABD vuông tại A
=>\(AB^2+AD^2=BD^2\)
=>\(BD=\sqrt{3^2+4^2}=5\left(cm\right)\)
\(BH\cdot BD=BA^2\)
=>\(BH=\dfrac{3^2}{5}=1,8\left(cm\right)\)
ΔAHB vuông tại H
=>\(AH^2+HB^2=AB^2\)
=>\(AH=\sqrt{3^2-1,8^2}=2,4\left(cm\right)\)