Gọi số tiền đơn vị 1,2,3 đóng góp lần lượt là a(triệu),b(triệu),c(triệu)

(Điều kiện: a>0; b>0; c>0)

Số tiền đóng góp của 3 đơn vị lần lượt tỉ lệ với 3;5;8 nên \(\dfrac{a}{3}=\dfrac{b}{5}=\dfrac{c}{8}\)

Tổng số tiền lãi là 256 triệu nên a+b+c=256

Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:

\(\dfrac{a}{3}=\dfrac{b}{5}=\dfrac{c}{8}=\dfrac{a+b+c}{3+5+8}=\dfrac{256}{16}=16\)

=>\(a=16\cdot3=48;b=16\cdot5=80;c=16\cdot8=128\)

vậy: Số tiền ba đơn vị đóng góp lần lượt là 48 triệu; 80 triệu; 128 triệu

\(E\left(x\right)=2x+1=0\)

\(\Rightarrow2x=-1\)

\(\Rightarrow x=-\dfrac{1}{2}\)

Vậy \(x=-\dfrac{1}{2}\) là nghiệm của đa thức

\(E\left(x\right)=0\Rightarrow2x+1=0\)

\(\Rightarrow2x=-1\)

\(\Rightarrow x=\dfrac{-1}{2}\)

Vậy...

a: Xét ΔBAH và ΔBDH có

BA=BD

AH=DH

BH chung

Do đó: ΔBAH=ΔBDH

b: ΔBAH=ΔBDH

=>\(\widehat{ABH}=\widehat{DBH}\)

Xét ΔBAE và ΔBDE có

BA=BD

\(\widehat{ABE}=\widehat{DBE}\)

BE chung

Do đó: ΔBAE=ΔBDE

=>EA=ED

=>ΔEAD cân tại E

c: ΔABC vuông tại A

=>\(\widehat{ABC}+\widehat{ACB}=90^0\)

=>\(\widehat{ACB}=30^0\)

Xét ΔEDC vuông tại D có \(sinECD=\dfrac{ED}{EC}\)

=>\(\dfrac{EA}{EC}=sin30=\dfrac{1}{2}\)

=>EC=2AE

vẽ hình nx nhé bạn

\(\left(x-3\right)\left(2x+4\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x-3=0\\2x+4=0\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=3\\x=-2\end{matrix}\right.\)

\(\left(x-3\right)\)\(\left(2x-4\right)\)\(=\) \(0\)

\(\Rightarrow\) \(\left(x-3\right)\)\(=\) \(0\)  hoặc \(\left(2x-4\right)\)\(=\) \(0\)

\(TH1:\) \(\left(x-3\right)\)\(=\) \(0\)

            \(x\)         \(=\) \(0\) \(+\) \(3\)

            \(x\)         \(=\) \(3\)

\(TH2:\) \(\left(2x+4\right)\)\(=\) \(0\)

            \(2x\)        \(=\) \(0\) \(-\) \(4\)

            \(2x\)        \(=\) \(-4\)

              \(x\)        \(=\)  \(-4\) \(:\) \(2\)

              \(x\)        \(=\) \(-2\)

Vậy \(x\) \(\in\) { \(3\) \(;\) \(-2\) }

a: Xét tứ giác ADHE có \(\widehat{ADH}+\widehat{AEH}=90^0+90^0=180^0\)

nên ADHE là tứ giác nội tiếp

Xét tứ giác BEDC có \(\widehat{BEC}=\widehat{BDC}=90^0\)

nên BEDC là tứ giác nội tiếp

b: Xét ΔADB vuông tại D và ΔAEC vuông tại E có

\(\widehat{DAB}\) chung

Do đó: ΔADB~ΔAEC

=>\(\dfrac{AD}{AE}=\dfrac{AB}{AC}\)

=>\(AD\cdot AC=AB\cdot AE\)

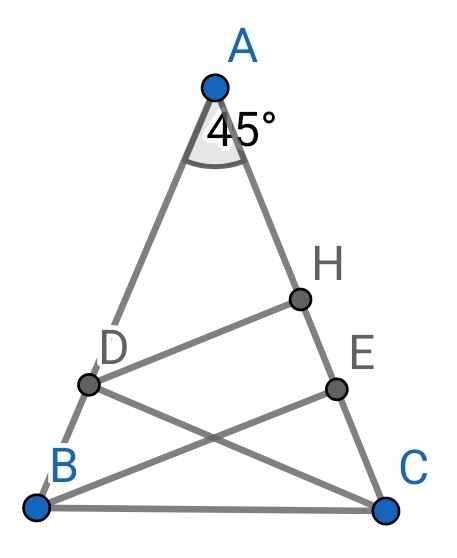
a) Do ∆ABC cân tại A (gt)

⇒ ∠ABC = ∠ACB = (180⁰ - ∠BAC) : 2

= (180⁰ - 45⁰) : 2

= 67,5⁰

Do ∠ABC = ∠ACB > ∠BAC (67,5⁰ = 67,5⁰ > 45⁰)

⇒ AC = AB > BC

b) Do ∠ABC = ∠ACB (cmt)

⇒ ∠DBC = ∠ECB

Xét ∆BCD và ∆CBE có:

BD = CE (gt)

∠DBC = ∠ECB (cmt)

BC là cạnh chung

⇒ ∆BCD = ∆CBE (c-g-c)

⇒ ∠BDC = ∠CEB (hai góc tương ứng)

a) Số học sinh loại giỏi:

120 . 1/6 = 20 (học sinh)

Số học sinh khá:

120 . 30% = 36 (học sinh)

Số học sinh trung bình:

120 . 1/3 = 40 (học sinh)

Số học sinh yếu:

120 - 20 - 36 - 40 = 24 (học sinh)

b) Tỉ số phần trăm của số học sinh yếu so với cả lớp:

24 . 100% : 120 = 20%

Có 7 cách chọn chữ số hàng đơn vị

Có 6 cách chọn chữ số hàng chục

Có 5 cách chọn chữ số hàng trăm

Số số tự nhiên có thể lập được là:

5.6.7 = 210 (số)

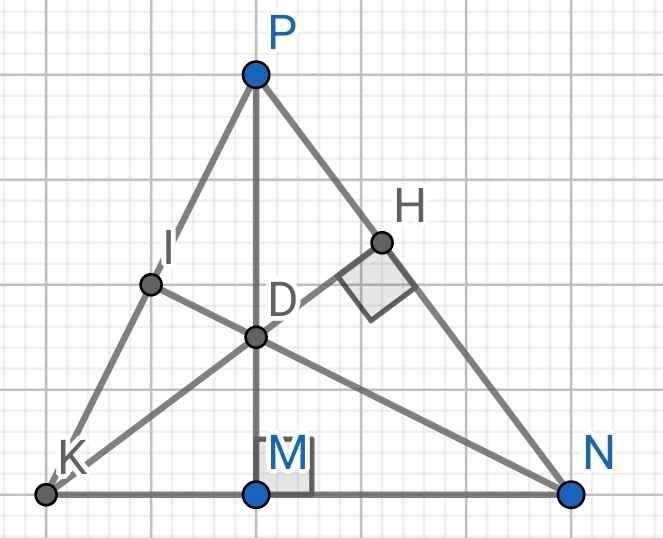
a) Do ND là đường phân giác của ∆MNP (gt)

⇒ ∠MND = ∠PND

⇒ ∠MND = ∠HND

Xét hai tam giác vuông: ∆MND và ∆HND có:

ND là cạnh chung

∠MND = ∠HND (cmt)

⇒ ∆MND = ∆HND (cạnh huyền - góc nhọn)

b) Do ∆MND = ∆HND (cmt)

⇒ MN = HN (hai cạnh tương ứng)

c) Do ∆MND = ∆HND (cmt)

⇒ MD = HD (hai cạnh tương ứng)

Xét hai tam giác vuông: ∆DMK và ∆DHP có:

MD = HD (cmt)

∠MDK = ∠HDP (đối đỉnh)

⇒ ∆DMK = ∆DHP (cạnh góc vuông - góc nhọn kề)

⇒ MK = HP (hai cạnh tương ứng)

Lại có: MN = HN (cmt)

⇒ MK + MN = HP + HN

⇒ KN = PN

⇒ ∆NPK cân tại N

Do ∆MNP vuông tại M (gt)

⇒ PM ⊥ MN

⇒ PM ⊥ NK

⇒ PM là đường cao của ∆NPK

Lại có:

DH ⊥ NP (gt)

⇒ KH ⊥ NP

⇒ KH là đường cao thứ hai của ∆NPK

⇒ ND là đường cao thứ ba của ∆NPK

Mà ∆NPK cân tại N (cmt)

⇒ ND cũng là đường trung tuyến của ∆NPK

⇒ ND đi qua trung điểm của PK

Mà I là trung điểm của PK

⇒ N, D, I thẳng hàng