Tìm nghiệm nguyên \(\left(x;y\right)\) của phương trình \(x^2=y\left(y+1\right)\left(y+2\right)\left(y+3\right)\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


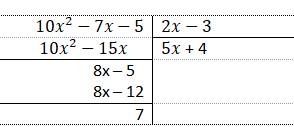
Để \(A⋮B\) thì \(7⋮\left(2x-3\right)\)
\(\Rightarrow2x-3\inƯ\left(7\right)=\left\{-7;-1;1;7\right\}\)
\(\Rightarrow2x\in\left\{-4;2;4;10\right\}\)
\(\Rightarrow x\in\left\{-2;1;2;5\right\}\)

\(x^2-4xy+5y^2-16=0\)
\(\Leftrightarrow\left(x-2y\right)^2+y^2=16\)
Ta xét các TH:
TH1: \(\left\{{}\begin{matrix}x-2y=0\\y=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=8\\y=4\end{matrix}\right.\)
TH2: \(\left\{{}\begin{matrix}x-2y=4\\y=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=4\\y=0\end{matrix}\right.\)
Vậy ta tìm được cặp số (x; y) là \(\left(8;4\right);\left(4;0\right)\)

\(3^x+4^x=5^x\left(1\right)\)
Ta thấy : \(x=1;pt\left(1\right)\Leftrightarrow3+4=5\left(loại\right)\)
\(x=2;pt\left(1\right)\Leftrightarrow9+16=25\left(thỏa\right)\)
vì \(pt\left(1\right):3^x+4^x=5^x\) chỉ có nghiệm \(x=2\) và vô nghiệm khi \(x>2\) (theo định lý fermat)
Vậy pt (1) chỉ có 1 nghiệm \(x=2\)

Đặt x = -2y + k (k \(\inℤ\))
Ta có x2 + 8y2 + 4xy - 2x - 4y = 4
<=> (-2y + k)2 + 8y2 + 4y(-2y + k) - 2(-2y + k) - 4y = 4
<=> k2 + 4y2 - 2k = 4
<=> (k - 1)2 + (2y)2 = 5 (*)
Dễ thấy (2y)2 \(⋮4\) (**)
Với y,k \(\inℤ\) kết hợp (*) ; (**) ta được
\(\left\{{}\begin{matrix}\left(k-1\right)^2=1\\\left(2y\right)^2=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}k=0\\k=2\end{matrix}\right.\\y=\pm1\end{matrix}\right.\)
Vậy (k,y) = (0;1) ; (0;-1) ; (2;1) ; (2;-1)
mà x = k - 2y nên các cặp (x;y) thỏa là (-2;1) ; (2;-1) ; (0;1) ; (4;-1)

\(y=x+\sqrt[]{2\left(1-x\right)}\left(x\le1\right)\)
\(\Rightarrow y=-\left(1-x\right)+\sqrt[]{2\left(1-x\right)}+1\)
\(\Rightarrow y=-\left(1-x\right)+\sqrt[]{2\left(1-x\right)}+1\)
\(\Rightarrow y=-\left[\left(1-x\right)-\sqrt[]{2\left(1-x\right)}+\left(\dfrac{\sqrt[]{2}}{2}\right)^2\right]+1+\left(\dfrac{\sqrt[]{2}}{2}\right)^2\)
\(\Rightarrow y=-\left[\sqrt[]{1-x}-\dfrac{\sqrt[]{2}}{2}\right]^2+1+\dfrac{1}{2}\)
\(\Rightarrow y=-\left[\sqrt[]{1-x}-\dfrac{\sqrt[]{2}}{2}\right]^2+\dfrac{3}{2}\)
mà \(-\left[\sqrt[]{1-x}-\dfrac{\sqrt[]{2}}{2}\right]^2\le0,\forall x\le1\)
\(\Rightarrow y=-\left[\sqrt[]{1-x}-\dfrac{\sqrt[]{2}}{2}\right]^2+\dfrac{3}{2}\le\dfrac{3}{2}\)
Dấu "=" xảy ra khi và chỉ khi
\(\sqrt[]{1-x}-\dfrac{\sqrt[]{2}}{2}=0\)
\(\Leftrightarrow\sqrt[]{1-x}=\dfrac{\sqrt[]{2}}{2}\)
\(\Leftrightarrow1-x=\dfrac{1}{2}\)
\(\Leftrightarrow x=1-\dfrac{1}{2}\)
\(\Leftrightarrow x=\dfrac{1}{2}\) (thỏa \(x\le1\))
\(\Rightarrow GTLN\left(y\right)=\dfrac{3}{2}\left(tạix=\dfrac{1}{2}\right)\)

ĐKXĐ : \(x\notin\left\{0;-1;-2;-3;-4\right\}\)
Ta có \(\dfrac{1}{x}+\dfrac{1}{x+1}+\dfrac{1}{x+2}+\dfrac{1}{x+3}+\dfrac{1}{x+4}=0\)
\(\Leftrightarrow\dfrac{2x+4}{x.\left(x+4\right)}+\dfrac{2x+4}{\left(x+1\right).\left(x+3\right)}+\dfrac{1}{x+2}=0\)
\(\Leftrightarrow\dfrac{2x+4}{\left(x+2\right)^2-4}+\dfrac{2x+4}{\left(x+2\right)^2-1}+\dfrac{1}{x+2}=0\) (*)
Đặt x + 2 = a \(\left(a\ne0\right)\)
(*) \(\Leftrightarrow\dfrac{2a}{a^2-4}+\dfrac{2a}{a^2-1}+\dfrac{1}{a}=0\)
\(\Leftrightarrow\dfrac{2}{a-\dfrac{4}{a}}+\dfrac{2}{a-\dfrac{1}{a}}+\dfrac{1}{a}=0\) (**)
Đặt \(\dfrac{1}{a}=b\left(b\ne0\right)\) \(\Rightarrow ab=1\)
Ta được (**) \(\Leftrightarrow\dfrac{2}{a-4b}+\dfrac{2}{a-b}+b=0\)
\(\Leftrightarrow\dfrac{2b}{1-4b^2}+\dfrac{2b}{1-b^2}+b=0\)
\(\Leftrightarrow\dfrac{2}{1-4b^2}+\dfrac{2}{1-b^2}=-1\)
\(\Rightarrow4-10b^2=-4b^4+5b^2-1\)
\(\Leftrightarrow4b^4-15b^2+5=0\) (***)
Đặt b2 = t > 0
Ta có (***) <=> \(4t^2-15t+5=0\Leftrightarrow t=\dfrac{15\pm\sqrt{145}}{8}\) (tm)
\(\Leftrightarrow b=\pm\sqrt{\dfrac{15\pm\sqrt{145}}{8}}\)
mà x + 2 = a ; ab = 1
nên \(x=\pm\sqrt{\dfrac{8}{15\pm\sqrt{145}}}-2\)
Thử lại ta có phương trình có 4 nghiệm như trên

Đồ thị hàn số y = a\(x\) + b đi qua các điểm A (\(\sqrt{2}\); 4 - \(\sqrt{2}\)) vàB (2; \(\sqrt{2}\))
Thay tọa độ điểm A, B vào pt đồ thị ta có:
\(\left\{{}\begin{matrix}\sqrt{2}.a+b=4-\sqrt{2}\\2a+b=2+\sqrt{2}\end{matrix}\right.\)
Trừ vế cho vế ta có: 2a + b - (\(\sqrt{2}\)a + b) = 2 + \(\sqrt{2}\) - (4 - \(\sqrt{2}\))
2a + b - \(\sqrt{2}\)a - b = -2 + 2\(\sqrt{2}\)
2a - \(\sqrt{2}\)a = - 2 + 2\(\sqrt{2}\)
a.(2 - \(\sqrt{2}\)) = -2 + 2\(\sqrt{2}\)
a = (-2 + 2\(\sqrt{2}\)) : (2 - \(\sqrt{2}\))
a = \(\sqrt{2}\)
b = 2 + \(\sqrt{2}\) - 2\(\sqrt{2}\)
b = 2 - \(\sqrt{2}\)

\(\left\{{}\begin{matrix}\left(P\right):y=x^2\\\left(d\right):y=-x+2\end{matrix}\right.\)
a) Tọa độ giao điểm của (P) và (Q) là nghiệm của hệ phương trình
\(\left\{{}\begin{matrix}y=x^2\\y=-x+2\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}y=x^2\\x^2=-x+2\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}y=x^2\\x^2+x-2=0\left(1\right)\end{matrix}\right.\)
\(pt\left(1\right)\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-2\end{matrix}\right.\) \(\left(a+b+c=1+1-2=0\right)\)
\(hpt\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x=1\\y=1\end{matrix}\right.\\\left\{{}\begin{matrix}x=-2\\y=4\end{matrix}\right.\end{matrix}\right.\)
Vậy tọa độ giao điểm của (P) và (Q) là \(A\left(1;1\right)\&B\left(-2;4\right)\)
a) Phương trình hoành độ giao điểm :
x2 = - x + 2
<=> (x - 1)(x + 2) = 0
<=> \(\left[{}\begin{matrix}x=1\\x=-2\end{matrix}\right.\)
Với x = 1 ta được y = 1
Với x = -2 ta được y = 4
Vậy tọa độ giao điểm là A(1; 1) ; B(-2;4)
b) Gọi C(-2 ; 0) ; D(1;0)
ta được \(S_{AOB}=S_{ABCD}-S_{BOC}-S_{AOD}\)
\(=\dfrac{\left(BC+AD\right).CD}{2}-\dfrac{BC.CO}{2}-\dfrac{AD.DO}{2}\)
\(=\dfrac{\left(4+1\right).3}{2}+\dfrac{4.2}{2}+\dfrac{1.1}{2}=12\) (đvdt)

O A x B C D E
D là giao của (O) với Ox; E là giao của Ox với (A)
Xét (A) có
\(sđ\widehat{COE}=\dfrac{1}{2}sđcungCE=\dfrac{1}{2}\left(sđcungOCE-sđcungCO\right)=\)
\(=\dfrac{1}{2}\left(180^o-sđcungCO\right)=90^o-\dfrac{1}{2}sđcungCO\) (1)
\(sđ\widehat{BCO}=\dfrac{1}{2}sđcungCO\) (góc giữa tiếp tuyến và dây cung)
Xét tg vuông BCO
\(sđ\widehat{BOC}=90^o-sđ\widehat{BCO}=90^o-\dfrac{1}{2}sđcungCO\) (2)
Xét tg CBO và tg CDO có
OB=OD (bán kính (O))
OC chung
Từ (1) và (2) \(\Rightarrow\widehat{BOC}=\widehat{COE}\)
=> tg CBO = tgCDO (c.g.c)\(\Rightarrow\widehat{CDO}=\widehat{CBO}=90^o\)
\(\Rightarrow CD\perp Ox\)
Ta có (O) cố định; Ox cố định => D cố định => đường thẳng đi qua C vuông góc với Ox tại D cố định
Vậy khi A di chuyển thì C luôn nằm trên đường thẳng vuông góc với Ox tại D
Ta có \(VP=y\left(y+3\right)\left(y+1\right)\left(y+2\right)\)
\(VP=\left(y^2+3y\right)\left(y^2+3y+2\right)\)
\(VP=\left(y^2+3y+1\right)^2-1\)
\(VP=t^2-1\) (với \(t=y^2+3y+1\ge0\))
pt đã cho trở thành:
\(x^2=t^2-1\)
\(\Leftrightarrow t^2-x^2=1\)
\(\Leftrightarrow\left(t-x\right)\left(t+x\right)=1\)
Ta xét các TH:
0
Xét TH \(\left(t,x\right)=\left(1,0\right)\) thì \(y^2+3y+1=1\) \(\Leftrightarrow\left[{}\begin{matrix}y=0\\y=-3\end{matrix}\right.\) (thử lại thỏa)
Xét TH \(\left(t,x\right)=\left(-1;0\right)\) thì \(y^2+3y+1=-1\Leftrightarrow\left[{}\begin{matrix}y=-1\\y=-2\end{matrix}\right.\) (thử lại thỏa).
Vậy các bộ số nguyên (x; y) thỏa mãn bài toán là \(\left(0;y\right)\) với \(y\in\left\{-1;-2;-3;-4\right\}\)