tính chiều cao AH của tam giác ABC biết diện tích tam giác bằng 20 cm2 độ dài đáy bằng 8 cm
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đổi: \(3dm=30cm\)
Diện tích xung quanh hộp là:
\(2\times\left(30+20\right)\times15=1500\) ( cm2 )
Diện tích tôn dùng để làm hộp là:
\(1500+30\times20=2100\) ( cm2 )
Đ/S:...

a: Vì \(AD=\dfrac{1}{3}AC\)
nên \(S_{ABD}=\dfrac{1}{3}\times S_{ABC}\)
=>\(\dfrac{S_{ABD}}{S_{ABC}}=\dfrac{1}{3}\)
b: Vì \(AE=\dfrac{2}{3}AB\)
nên \(S_{AED}=\dfrac{2}{3}\times S_{ABD}=\dfrac{2}{9}\times S_{ABC}\)
=>\(S_{ABC}=4,5\times S_{AED}=4,5\times8=36\left(cm^2\right)\)

CN=3NA
=>\(\dfrac{NA}{NC}=\dfrac{1}{3}\)
E,N,M thẳng hàng
=>\(\dfrac{EA}{EB}\times\dfrac{NC}{NA}\times\dfrac{MB}{MC}=1\)
=>\(\dfrac{EA}{EB}\times3=1\)
=>\(\dfrac{EA}{EB}=\dfrac{1}{3}\)
=>\(\dfrac{EA}{AB}=\dfrac{1}{2}\)
=>AB=2EA
=>\(S_{NAB}=2\times S_{NEA}=54\left(cm^2\right)\)
Vì NC=3NA
nên \(\dfrac{AN}{AC}=\dfrac{1}{4}\)
=>AC=4AN
=>\(S_{ABC}=4\times S_{ABN}=216\left(cm^2\right)\)

Olm chào em, em sử dụng phần mềm hình học em nhé.

mà thui bạn thì tao giúp
450x0,45+1,5x30x3+5x9x2,5
=45x(10x0,45)+1,5x30x3+5x9x2,5
=45x4,5+45x3+45x2,5
=45x(3+45+2,5)
=45x10
=450
Lần sao tự làm nghe

Bài 1:
\(B=\left(\dfrac{178}{179}+\dfrac{179}{180}+\dfrac{180}{181}\right)\times\left(\dfrac{80}{56}-\dfrac{15}{12}:\dfrac{7}{8}\right)\)
\(=\left(\dfrac{178}{179}+\dfrac{179}{180}+\dfrac{180}{181}\right)\times\left(\dfrac{10}{7}-\dfrac{5}{4}\times\dfrac{8}{7}\right)\)
\(=\left(\dfrac{178}{179}+\dfrac{179}{180}+\dfrac{180}{181}\right)\times\left(\dfrac{10}{7}-\dfrac{10}{7}\right)\)
=0
Bài 2:
Tổng của hai số là 77x2=154
Nếu viết thêm vào bên phải của số thứ nhất một chữ số 0 thì được số thứ hai thì có nghĩa là số thứ hai bằng 10 lần số thứ nhất
Số thứ hai là 154:11x10=140
Số thứ nhất là 154-140=14

Bạn Bình có số cái kẹo là:
(48-12):2=18(cái)
Bạn An có số cái kẹo là:
48-18=30(cái)
Đáp số: Bạn Bình:18 cái kẹo
Bạn An:30 cái kẹo
Bổ sung cho @ Vu Duy.
Sơ đồ đoạn thẳng: 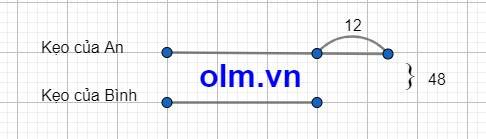

\(\dfrac{1}{1+2}+\dfrac{1}{1+2+3}+...+\dfrac{1}{1+2+3+...+2022}+\dfrac{2}{x}=2\)
=>\(\dfrac{1}{2\text{x}\dfrac{3}{2}}+\dfrac{1}{3\text{x}\dfrac{4}{2}}+...+\dfrac{1}{2022\text{x}\dfrac{2023}{2}}+\dfrac{2}{x}=2\)
=>\(\dfrac{2}{2\text{x}3}+\dfrac{2}{3\text{x}4}+...+\dfrac{2}{2022\text{x}2023}+\dfrac{2}{x}=2\)
=>\(\dfrac{1}{2\text{x}3}+\dfrac{1}{3\text{x}4}+...+\dfrac{1}{2022\text{x}2023}+\dfrac{1}{x}=1\)
=>\(\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{2022}-\dfrac{1}{2023}+\dfrac{1}{x}=1\)
=>\(\dfrac{1}{2}-\dfrac{1}{2023}+\dfrac{1}{x}=1\)
=>\(\dfrac{1}{x}=1-\dfrac{1}{2}+\dfrac{1}{2023}=\dfrac{1}{2}+\dfrac{1}{2023}=\dfrac{2025}{4046}\)
=>\(x=\dfrac{4046}{2025}\)
\(\dfrac{1}{1+2}\) + \(\dfrac{1}{1+2+3}\) + ... + \(\dfrac{1}{1+2+3+4+...+2022}\) + \(\dfrac{2}{x}\) = 2
\(\dfrac{1}{\left(1+2\right)\times2:2}\) + \(\dfrac{1}{\left(1+3\right)\times3:2}\)+ ... + \(\dfrac{1}{\left(1+2022\right)\times2022:2}\) + \(\dfrac{2}{x}\) = 2
\(\dfrac{2}{2\times3}\) + \(\dfrac{2}{3\times4}\) + ... + \(\dfrac{2}{2022\times2023}\) + \(\dfrac{2}{x}\) = 2
2 x (\(\dfrac{1}{2\times3}\) + \(\dfrac{1}{3\times4}\) + ... + \(\dfrac{1}{2022\times2023}\)) + \(\dfrac{2}{x}\) = 2
2 \(\times\) (\(\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{2022}-\dfrac{1}{2023}\)) + \(\dfrac{2}{x}\) = 2
2 \(\times\) (\(\dfrac{1}{2}\) - \(\dfrac{1}{2023}\)) + \(\dfrac{2}{x}\) = 2
2 x \(\dfrac{1011}{2023}\) + \(\dfrac{2}{x}\) = 2
\(\dfrac{2021}{2023}\) + \(\dfrac{2}{x}\) = 2
\(\dfrac{2}{x}\) = 2 - \(\dfrac{2021}{2023}\)
\(\dfrac{2}{x}\) = \(\dfrac{2025}{2023}\)
\(x\) = 2 : \(\dfrac{2025}{2023}\)
\(x\) = \(\dfrac{4046}{2025}\)

\(\dfrac{5}{1\times4}+\dfrac{5}{4\times7}+\dfrac{5}{7\times10}+\dfrac{5}{10\times13}+\dfrac{5}{13\times16}\)
\(=\dfrac{5}{3}\times\left(\dfrac{1}{1\times4}+\dfrac{1}{4\times7}+\dfrac{1}{7\times10}+\dfrac{1}{10\times13}+\dfrac{1}{13\times16}\right)\)
\(=\dfrac{5}{3}\times\left(1-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{7}+...+\dfrac{1}{13}-\dfrac{1}{16}\right)\)
\(=\dfrac{5}{3}\times\left(1-\dfrac{1}{16}\right)\)
\(=\dfrac{5}{3}\times\dfrac{15}{16}=\dfrac{25}{16}\)
\(0,9\times438\times2+1,8\times562+400\)
\(=1,8\times438+1,8\times562+400\)
\(=1,8\times\left(438+562\right)+400\)
\(=1,8\times1000+400\)
\(=1800+400\)
\(=2200\)

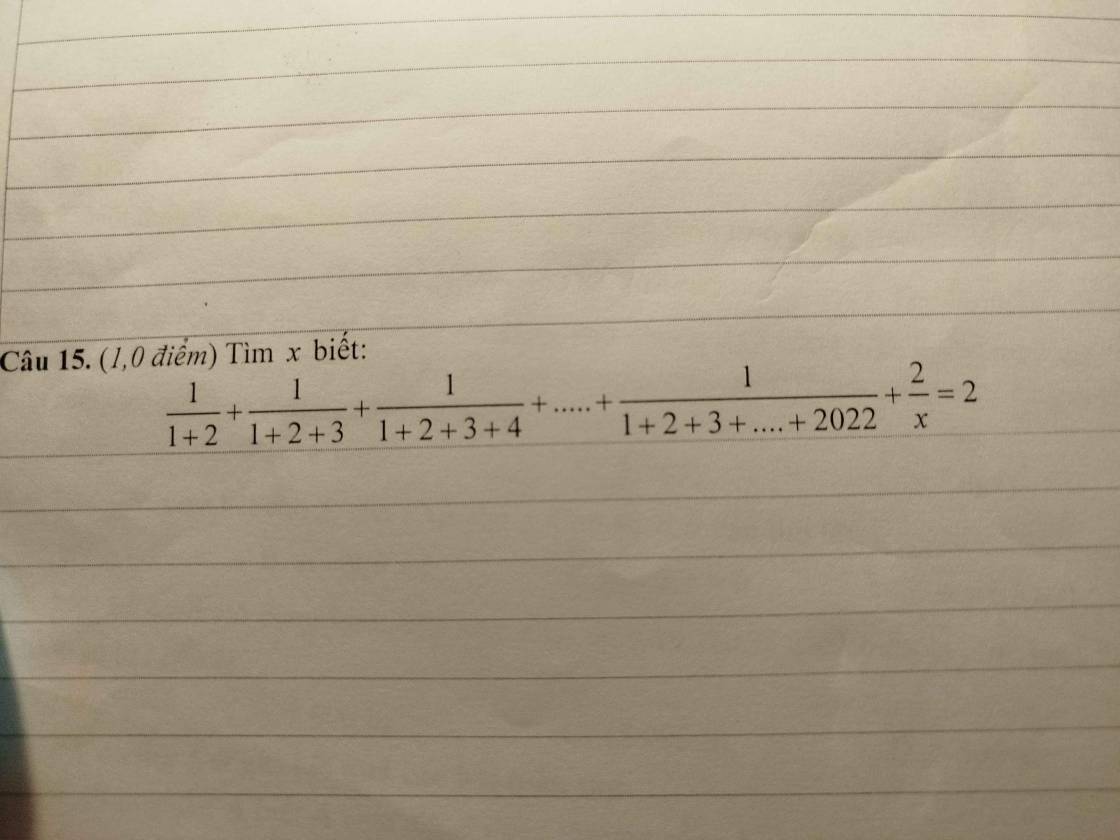
Chiều cao AH của tam giác là:
\(20:\left(\dfrac{1}{2}\times8\right)=5\) ( cm )
Đ/S:...
5cm nha