Đặt : \(\frac{x}{2}=\frac{y}{3}=\frac{z}{4}=k\)   \(\Rightarrow\hept{\begin{cases}x=2k\\y=3k\\z=4k\end{cases}}\)

Thay vào : \(x^2-y^2+2.z^2=108\)ta có :

\(\left(2k\right)^2-\left(3k\right)^2+2.\left(4k\right)^2=108\)

\(2^2.k^2-3^2.k^2+2.4^2.k^21=108\)

\(4.k^2-9.k^2+2.16.k^2=108\)

\(4.k^2-9.k^2+32.k^2=108\)

\(\left(4-9+32\right).k^2=108\)

\(27.k^2=108\)

\(k^2=4\)

\(k^2=\left(2\right)^2\)hoặc \(\left(-2\right)^2\)

\(k=\pm2\)

* ) Nếu \(k=2\)thì :   \(\Rightarrow\hept{\begin{cases}x=2.2=4\\y=3.2=6\\z=4.2=8\end{cases}}\)

* ) Nếu \(k=-2\)thì :   \(\Rightarrow\hept{\begin{cases}x=2.\left(-2\right)=-4\\y=3.\left(-2\right)=-6\\z=4.\left(-2\right)=-8\end{cases}}\)

Vậy ........

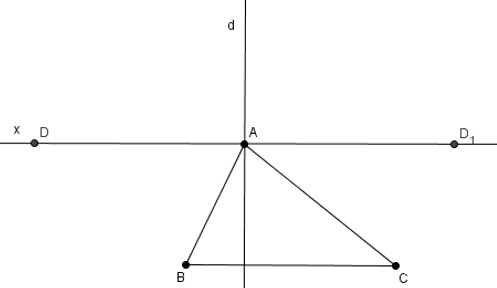
Cách vẽ:

- Vẽ đường thẳng d qua A và vuông góc với BC.

- Vẽ đường thẳng Ax vuông góc với đường thẳng d tại A. Khi đó ta có được đường thẳng Ax song song với BC (hai cặp góc so le trong tạo thành đều là góc vuông).

- Trên đường thẳng Ax đặt đoạn thẳng AD có độ dài bằng độ dài đoạn thẳng BC. Ta được đoạn AD cần vẽ (có 2 điểm D thỏa mãn).

Bài 2 :

a) \(\left(5x+1\right)^2=\frac{36}{49}\)

\(\Rightarrow\orbr{\begin{cases}\left(5x+1\right)^2=\left(\frac{6}{7}\right)^2\\\left(5x+1\right)^2=\left(\frac{-6}{7}\right)^2\end{cases}}\)

\(\Rightarrow\orbr{\begin{cases}5x+1=\frac{6}{7}\\5x+1=\frac{-6}{7}\end{cases}}\)

\(\Rightarrow\orbr{\begin{cases}5x=\frac{-1}{7}\\5x=\frac{-13}{7}\end{cases}}\)

\(\Rightarrow\orbr{\begin{cases}x=\frac{-1}{35}\\x=\frac{-13}{35}\end{cases}}\)

b) \(\left(x-\frac{2}{9}\right)^3=\left(\frac{2}{3}\right)^6\)

\(\Rightarrow\left(x-\frac{2}{9}\right)^3=\left[\left(\frac{2}{3}\right)^2\right]^3\)

\(\Rightarrow\left(x-\frac{2}{9}\right)^3=\left(\frac{4}{9}\right)^3\)

\(\Rightarrow x-\frac{2}{9}=\frac{4}{9}\)

\(\Rightarrow x=\frac{2}{3}\)

c) ( x - 2 )³ = 64

=> ( x - 2 )³ = 4³

=> x - 2 = 4

=> x = 6

d) \(\left(x-3,5\right)^2+\left(y-\frac{1}{10}\right)^4\le0\)

Vì \(\hept{\begin{cases}\left(x-3,5\right)^2\ge0\forall x\\\left(y-\frac{1}{10}\right)^4\ge0\forall y\end{cases}}\)

\(\Rightarrow\left(x-3,5\right)^2+\left(y-\frac{1}{10}\right)^4\ge0\)

Dấu "=" xảy ra \(\Leftrightarrow\hept{\begin{cases}\left(x-3,5\right)^2=0\\\left(y-\frac{1}{10}\right)^4=0\end{cases}}\)\(\Leftrightarrow\hept{\begin{cases}x-3,5=0\\y-\frac{1}{10}=0\end{cases}}\)

\(\Leftrightarrow\hept{\begin{cases}x=3,5\\y=\frac{1}{10}\end{cases}}\)

Bài 3 :

a) Ta có : 2²⁴  = ( 2³ )⁸ = 8⁸ < 9⁸ = ( 3² )⁸ = 3¹⁶

=> 2²⁴ < 3¹⁶

b) Ta có : ( -5 )⁹ < 0 < ( -2 )¹⁸

=> ( -5 )⁹ < ( -2 )¹⁸

a, góc B1 = góc A1 = \(105^o\)( slt)

mà góc A1 = \(\frac{7}{5}\)A2

=> \(105^o\)=\(\frac{7}{5}\).A2

=>A2 = \(105^o:\frac{7}{5}=75^o\)

\(\left||x+3\right|-10|=20\)

\(\Rightarrow\orbr{\begin{cases}\left|x+3\right|-10=20\\\left|x+3\right|-10=-20\end{cases}}\Rightarrow\orbr{\begin{cases}\left|x+3\right|=30\\\left|x+3\right|=-10\end{cases}}\)

Ta có: \(\left|x+3\right|\ge0\forall x\)

\(\Rightarrow\left|x+3\right|\ne-10\)

\(\Rightarrow\left|x+3\right|=30\Rightarrow\orbr{\begin{cases}x+3=30\\x+3=-30\end{cases}}\Rightarrow\orbr{\begin{cases}x=27\\x=-33\end{cases}}\)

|| x + 3 | - 10 | = 20

\(\Rightarrow\orbr{\begin{cases}\left|x+3\right|-10=20\\\left|x+3\right|-10=-20\end{cases}}\)

\(\Rightarrow\orbr{\begin{cases}\left|x+3\right|=30\\\left|x+3\right|=-10\end{cases}}\)mà | x + 3 | ≥ 0 ∀ x

=> | x + 3 | = 30

\(\Rightarrow\orbr{\begin{cases}x+3=30\\x+3=-30\end{cases}}\)

\(\Rightarrow\orbr{\begin{cases}x=27\\x=-33\end{cases}}\)

( x - 1 )³ = ( x - 1 )⁵

=> ( x - 1 )⁵ - ( x - 1 )³ = 0

=> ( x - 1 )³ . [ ( x - 1 )² - 1 ] = 0

\(\Rightarrow\orbr{\begin{cases}\left(x-1\right)^3=0\\\left(x-1\right)^2-1=0\end{cases}}\)

\(\Rightarrow\orbr{\begin{cases}x-1=0\\\left(x-1\right)^2=1\end{cases}}\)

\(\Rightarrow\orbr{\begin{cases}x=1\\x-1\in\left\{-1;1\right\}\end{cases}}\)

\(\Rightarrow\orbr{\begin{cases}x=1\\x\in\left\{0;2\right\}\end{cases}}\)