Tìm x biết (1 phần 4 trừ x) mũ 2 trừ 125% = hỗn số 1 13 phần 16
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\left(5.2^{13}.2^{22}-2^{36}\right):2^{34}\)
\(=\left(5.2^{35}-2^{36}\right):2^{34}\)
\(=5.2^{35}:2^{34}-2^{36}:2^{34}\)
\(=5.2-2^2\)
\(=10-4\)
\(=6\)

Từ điều kiện đã cho, chia cả 2 vế cho 2, ta thu được \(1+2+3+...+\left(n-1\right)+n=105\) (1)
Ta sẽ chứng minh \(1+2+3+...+n=\dfrac{n\left(n+1\right)}{2}\) (*). Thật vậy, với \(n=1\) thì (*) đúng.
Giả sử (*) đúng đến \(n=k\left(k\ge1\right)\). Khi đó \(1+2+3+...+k=\dfrac{k\left(k+1\right)}{2}\)
Ta cần chứng minh (*) đúng với \(n=k+1\), tức là chứng minh \(1+2+3+...+k+\left(k+1\right)=\dfrac{\left(k+1\right)\left(k+2\right)}{2}\). Thật vậy, với \(n=k+1\) thì \(1+2+3+...+k+\left(k+1\right)=\dfrac{k\left(k+1\right)}{2}+\left(k+1\right)\) (giả thiết quy nạp)
\(=\dfrac{k\left(k+1\right)+2\left(k+1\right)}{2}=\dfrac{\left(k+1\right)\left(k+2\right)}{2}\). Như vậy ta đã chứng minh được (*) đúng với \(n=k+1\)
Từ đó ta có điều phải chứng minh. Thay vào (1), ta có \(\dfrac{n\left(n+1\right)}{2}=105\Leftrightarrow n^2+n-210=0\) \(\Leftrightarrow\left[{}\begin{matrix}n=14\left(nhận\right)\\n=-15\left(loại\right)\end{matrix}\right.\).
Vậy số tự nhiên n thỏa mãn đề bài là \(n=14\)

Bài 12 : Tính tổng đại số sau một cách hợp lý .
d) 1-3-5+7-9-11+...+1000-1002-1004
Số hạng của dãy:
Vậy có tất cả:
Vậy


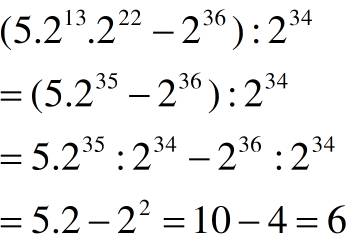
(\(\dfrac{1}{4}\) - x)2 - 125% = \(1\dfrac{13}{16}\)
⇒ (\(\dfrac{1}{4}\) - x)2 - \(\dfrac{5}{4}\) = \(\dfrac{29}{16}\)
⇒ (\(\dfrac{1}{4}\) - x)2 = \(\dfrac{29}{16}\) + \(\dfrac{5}{4}\)
⇒ (\(\dfrac{1}{4}\) - x)2 = \(\dfrac{49}{16}\)
⇒ (\(\dfrac{1}{4}\) - x)2 = \(\left(\dfrac{7}{4}\right)^2\)= \(\left(\dfrac{-7}{4}\right)^2\)
⇒ \(\dfrac{1}{4}\) - x = \(\dfrac{7}{4}\); \(\dfrac{1}{4}\) - x = \(\dfrac{-7}{4}\)
* TH1 :
\(\dfrac{1}{4}\) - x = \(\dfrac{7}{4}\)
⇒ x = \(\dfrac{1}{4}-\dfrac{7}{4}\)
⇒ x = \(\dfrac{-6}{4}\) = \(\dfrac{-3}{2}\)
* TH2 :
\(\dfrac{1}{4}\) - x = \(\dfrac{-7}{4}\)
⇒ x = \(\dfrac{1}{4}-\dfrac{-7}{4}\)
⇒ x = \(\dfrac{8}{4}\) = 2
vậy x ϵ \(\left\{\dfrac{-3}{2};2\right\}\)