Tìm giá trị lớn nhất: \(D=\dfrac{2\sqrt{a}}{a+1}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bạn nên viết đề bằng công thức toán (biểu tượng $\sum$ góc trái khung soạn thảo) để mọi người hiểu đề của bạn hơn nhé.


Bài `1`
\(A=\sqrt{8-2\sqrt{15}}-\sqrt{8+2\sqrt{15}}\\ =\sqrt{3-2\sqrt{15}+5}-\sqrt{3+2\sqrt{15}+5}\\ =\sqrt{\left(\sqrt{3}\right)^2-2\sqrt{3}\sqrt{5}+\left(\sqrt{5}\right)^2}-\sqrt{\left(\sqrt{3}\right)^2+2\sqrt{3}\sqrt{5}+\left(\sqrt{5}\right)^2}\\ =\sqrt{\left(\sqrt{3}-\sqrt{5}\right)^2}-\sqrt{\left(\sqrt{3}+\sqrt{5}\right)^2}\\ =\left|\sqrt{3}-\sqrt{5}\right|-\left|\sqrt{3}+\sqrt{5}\right|\\ =\sqrt{5}-\sqrt{3}-\sqrt{5}-\sqrt{3}\\ =-2\sqrt{3}\)
\(B=\sqrt{2-\sqrt{3}}-\sqrt{2+\sqrt{3}}\\ B-\sqrt{2}=\left(\sqrt{2-\sqrt{3}}-\sqrt{2+\sqrt{3}}\right)\cdot\sqrt{2}\\ =\sqrt{2-\sqrt{3}}\cdot\sqrt{2}-\sqrt{2+\sqrt{3}}\cdot\sqrt{2}\\ =\sqrt{\left(2-\sqrt{3}\right)\cdot2}-\sqrt{\left(2+\sqrt{3}\right)\cdot2}\\ =\sqrt{4-2\sqrt{3}}-\sqrt{4+2\sqrt{3}}\\ =\sqrt{3-2\sqrt{3}+1}-\sqrt{3+2\sqrt{3}+1}\\ =\sqrt{\left(\sqrt{3}\right)^2-2\sqrt{3}\cdot1+1^2}-\sqrt{\left(\sqrt{3}\right)^2+2\sqrt{3}\cdot2+1^2}\\ =\sqrt{\left(\sqrt{3}-1\right)^2}-\sqrt{\left(\sqrt{3}+1\right)^2}\\ =\left|\sqrt{3}-1\right|-\left|\sqrt{3}+1\right|\\ =\sqrt{3}-1-\sqrt{3}-1\\ =-2\)
Mà \(A-\sqrt{2}=-2\)
\(\Rightarrow A=\dfrac{-2}{\sqrt{2}}=\dfrac{-\left(\sqrt{2}\right)^2}{\sqrt{2}}=-\sqrt{2}\)
2) \(C=x-\sqrt{x-3}\)
\(C=\left(x-3\right)-\sqrt{x-3}+3\)
Đặt \(\sqrt{x-3}=t\left(t\ge0\right)\)
\(C=t^2-t+3\)
\(C=t^2-2t.\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{11}{4}\)
\(C=\left(t-\dfrac{1}{2}\right)^2+\dfrac{11}{4}\) \(\ge\dfrac{11}{4}\)
Dấu "=" xảy ra \(\Leftrightarrow t=\dfrac{1}{2}\Leftrightarrow\sqrt{x-3}=\dfrac{1}{2}\Leftrightarrow x=\dfrac{13}{4}\)
Vậy GTNN của C là \(\dfrac{11}{4}\)

\(\left(\dfrac{\sqrt{x}}{\sqrt{x}-1}-\dfrac{1}{x-\sqrt{x}}\right):\left(\dfrac{1}{\sqrt{x}+1}+\dfrac{2}{x-1}\right)\\ =\left(\dfrac{\sqrt{x}}{\sqrt{x}-1}-\dfrac{1}{\sqrt{x}\left(\sqrt{x}-1\right)}\right):\left(\dfrac{1}{\sqrt{x}+1}+\dfrac{2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\right)\\ =\left(\dfrac{\sqrt{x}\cdot\sqrt{x}}{\sqrt{x}\left(\sqrt{x}-1\right)}-\dfrac{1}{\sqrt{x}\left(\sqrt{x}-1\right)}\right):\left(\dfrac{\sqrt{x}-1}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}+\dfrac{2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\right)\\ =\dfrac{x-1}{\sqrt{x}\left(\sqrt{x}-1\right)}:\dfrac{\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{x-1}{\sqrt{x}\left(\sqrt{x}-1\right)}\cdot\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{\sqrt{x}+1}\\ =\dfrac{x-1}{\sqrt{x}}\)


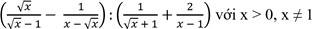
Min D = 0 tại a =0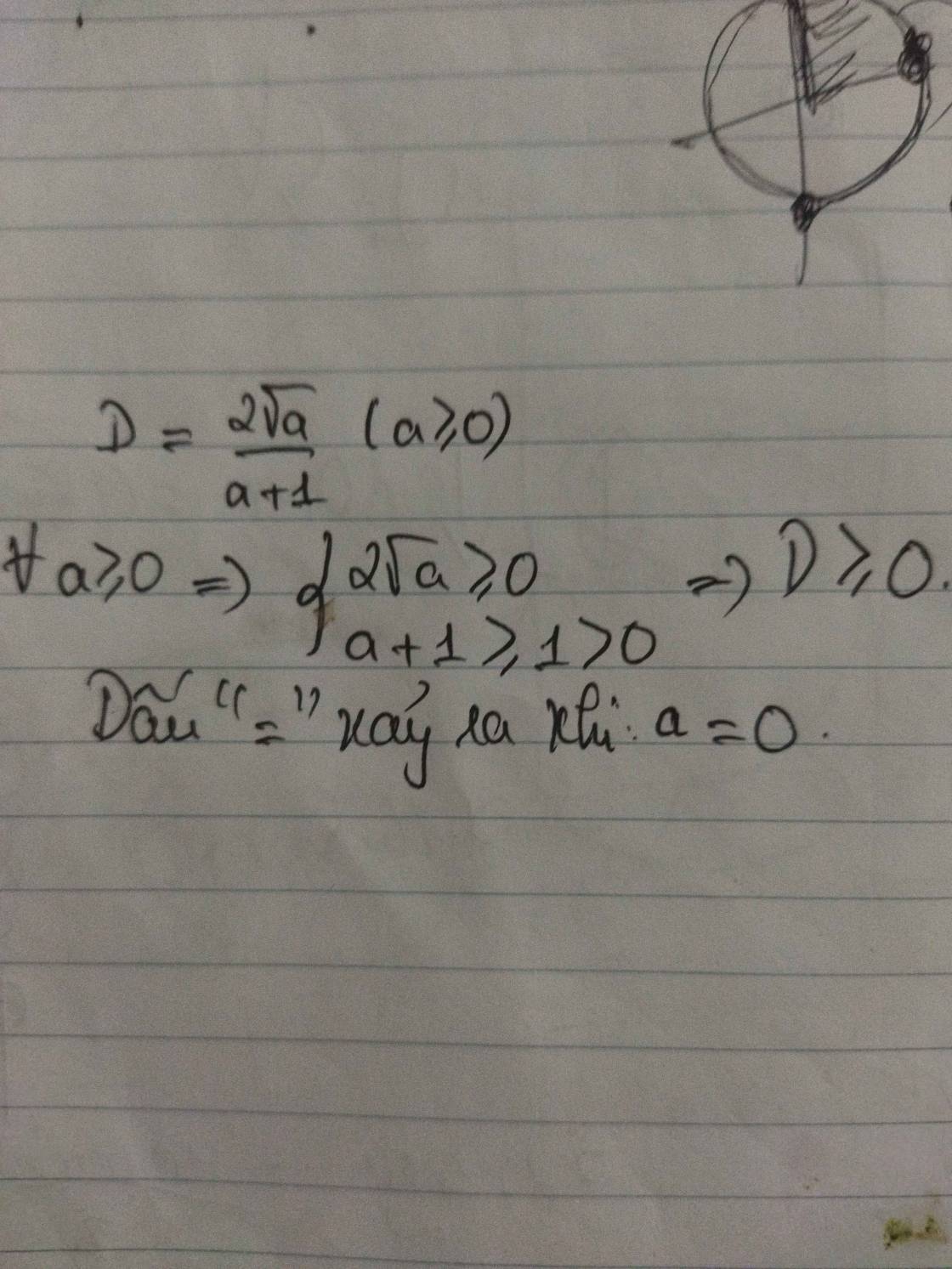
DK: a≥0
Với dk ta có \(a+1\ge2\sqrt{a}\Leftrightarrow\dfrac{2\sqrt{a}}{a+1}\le1\)
Vậy GTLN của D là 1 khi a=1(Bất đẳng thức Cô si)