b) 756x+243y=30147
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Vì 2x=3y =>x/3 = y/2 = x/15 = y/10
3y=5z=> y/ 5= z/3= y/10= z/6
=> x/15=y/10= z/6
áp dụng tính chất của dãy tỉ số bằng nhau ta có:
x/15= y/10 =z/6 = x-y+z/ 15-10+6 = -33/ 11= -3
vậy x= 15x(-3) = -45
y= -3x10= -30
z= 6x(-3)= -18
mà 2,3,5 cùng dấu=>x =-45 ; y=-30; z=-18 hoặc x=45; y=30; z=18
Vậy x= -45 thì y=-30 và z=-18 hoặc x=45 thì y=30 và z=18
chúc bạn hok tốt phần b, e cx tương tự nhé!!!!!!!!! đúng 100% lun nha(^+ ^)
b, Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\frac{x}{3}=\frac{y}{4}=\frac{z}{5}=\frac{-x-y+z}{-3-4+5}=\frac{16}{-2}=\left(-8\right)\)
\(\Rightarrow\hept{\begin{cases}\frac{x}{3}=\left(-8\right)\Rightarrow x=\left(-24\right)\\\frac{y}{4}=\left(-8\right)\Rightarrow y=\left(-32\right)\\\frac{z}{5}=\left(-8\right)\Rightarrow z=\left(-40\right)\end{cases}}\)
Vậy ....
d, Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\frac{x}{2}=\frac{y}{3}=\frac{z}{4}=\frac{x+2y-3z}{2+2.3-3.3}=\frac{-30}{-1}=30\)
\(\Rightarrow\hept{\begin{cases}\frac{x}{2}=30\Rightarrow x=60\\\frac{y}{3}=30\Rightarrow y=90\\\frac{z}{4}=30\Rightarrow z=120\end{cases}}\)
Vậy ...

a. ta có :
\(k=\frac{y}{x}=\frac{12}{8}=\frac{3}{2}\)
vậy \(y=\frac{3}{2}\times x\)
khi x=2 thì y=3
khi x=-4 thì y =- 6


(2 ^2010 +1)/(2 ^2017 +1) và (2 ^2012 +1)/(2 ^2009 +1)
Trả lời :
(2 ^2010 +1)/(2 ^2017 +1) < (2 ^2012 +1)/(2 ^2009 +1)
HC T bài này khó đó
ta có:
\(\left(2^{2010}+1\right)>\left(2^{2009}+1\right)>1\) và \(\left(2^{2017}+1\right)>\left(2^{2012}+1\right)>1\)
thế nên
\(\left(2^{2010}+1\right)\left(2^{2017}+1\right)>\left(2^{2012}+1\right)\left(2^{2009}+1\right)\)

Câu 1
a) Vì m vuông góc vớiAB }=> m// n
N vuông góc với AB
Vậy...
b) vì m//n(a)
=> ADC +C1=180°( 2 góc trong cùng phía)
=>120°+C1=180°
=> C1
=60°
Vậy...

Gọi số táo ; cam và nho lần lượt là a ; b ; c ( quả ) ( a , b , c ∈ N* ) và lần lượt tỉ lệ với 4 ; 7 ; 9
Theo bài ra , ta có :
5a - b - c = 16
\(\frac{a}{4}=\frac{b}{7}=\frac{c}{9}\)
Áp dụng tính chất dãy tỉ số bằng nhau , ta có :
\(\frac{a}{4}=\frac{b}{7}=\frac{c}{9}=\frac{5a}{20}=\frac{5a-b-c}{20-7-9}=\frac{16}{4}=4\)
\(\Rightarrow\hept{\begin{cases}a=4.4=16\\b=4.7=28\\c=4.9=36\end{cases}}\)

\(3^{24}< 3^{25}=\left(3^5\right)^5=243^5< 625^5=\left(5^4\right)^5=5^{20}\)
suy ra \(3^{24}< 5^{20}\).


 pls
pls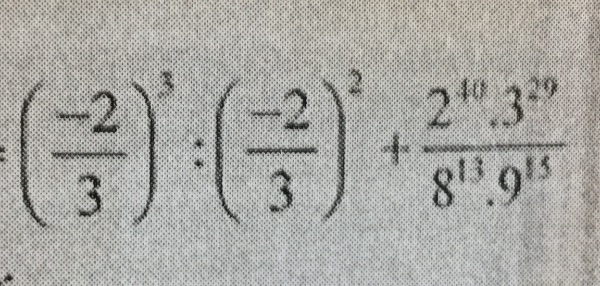
 ới ạ đang gấp lắm
ới ạ đang gấp lắm
 các bạn giúp mình với mình đang cần gấp
các bạn giúp mình với mình đang cần gấp
Nhanh thì mình kick cho