Một máy tính hiển thị 2/9 để chỉ ngày mùng 9 tháng 2, trong khi những máy
tính khác hiển thị 2/9 để chỉ ngày mùng 2 tháng 9. Điều này gây nhầm lẫn vì khi nhìn
vào 2/9, ta sẽ không biết đó là ngày mùng 9 tháng 2 hay mùng 2 tháng 9.
Tuy nhiên đối với 4/30 hoặc 30/4, ta có thể hiểu ngay đó là ngày 30 tháng 4 vì một năm
chỉ có 12 tháng. Hỏi trong một năm có bao nhiêu ngày có thể gây ra sự nhầm lẫn như
trên?
Trả lời: Có ....ngày.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có:
aaaaaa = 100000a + 10000a + 1000a + 100a + 10a + a
= 111000a + 111a
⇒ aaaaaa : 3a
= 111000a : 3a + 111a : 3a
= 37000 + 37
= 37037

Giải: 1,8 km = 1800 m
a; Trên đoạn đường đó có số cột điện là: 1800 : 60 + 1 = 31(cột điện)
b; Những cột không phải trồng lại là những cột có khoảng cách bằng bội chung nhỏ nhất của 40 và 60
40 = 23.5; 60 = 22.5.3; BCNN(40; 60) = 23.5.3 = 120
Số cột điện không phải trồng lại là: 1800 : 120 + 1 = 16 (cột điện)
Kết luận: Trên đoạn đường đó nếu trồng các cột điện mà mỗi cột cách nhau 40 m và cả hai đầu đều có cột điện thì số cột không phải trồng lại là 16 cột điện.

Diện tích toàn phần của hình hộp là:
\(64:32\%=200\left(m^2\right)\)
Độ dài cạnh đáy là \(\sqrt{64}=8\left(m\right)\)
Chu vi đáy là \(8\times4=32\left(m\right)\)
Diện tích xung quanh của hình hộp là:
\(200-2\times64=72\left(m^2\right)\)
Chiều cao của hình hộp là:
72:32=2,25(m)
Giải:
Diện tích toàn phần của hình hộp chữ nhật là:
64 : 32 x 100 = 200 (m2)
Diện hai mặt đáy là: 64 x 2 = 128 (m2)
Diện tích xung quanh của hình hộp chữ nhật là: 200 - 128 = 72 (m2)
Vì 64 = 8 x 8
Vậy cạnh đáy là: 8 m
Chu vi đáy của hình hộp chữ nhật là: 8 x 4 = 32 (m)
Chiều cao của hình hộp chữ nhật là: 72 : 32 = 2,25 (m)
Đáp số: 2,25 m

a. M(x) = x² + 2x – 3 + x² - 9x + 5
= 2x2 - 7x + 2
N(x) = x² + 2x – 3 - x² + 9x - 5
= 11x - 8

Bài toán trở thành: Cho 1 tập các số tự nhiên A= {1;2;3...100] ϵ N. Tìm tập con B ⊂ A thỏa mãn: Hiệu giữa Tổng các phần tử của A và Tổng các phần tử của A bằng 4982.
1/. Ta tính được: Tổng các phần tử của A là Sa=1+2+3+ ... +100
Sa = 100*(100+1)/2 = 5050
2/. Suy ra Tổng các phần tử của B sẽ là: Sb = Sa-4982
Sb = 5050 - 4982 = 68
3/. Giả sử Phần tử đầu tiên của B (chính là trang đầu tiên trong các trang bị mất) là (B1+1), và B có n phần tử.
Khi đó: B = {B1+1; B1+2... B1+n} và Tổng các phần tử của B là Sb= n*[(B1+1) + (B1+n)] / 2
Hay Sb = n*(2*B1 + n +1)/2 ==> 68 = n*(2*B1 + n +1)/2
==> 2n*B1 + n(n+1) = 136 ==> n*(2*B1 + n +1) = 136 (*)
Ta thấy: n và (2*B1 + n +1) là 2 số tự nhiên khác tính chẵn lẻ.
Tức là ∀ n ∈ N: Khi n chẵn thì (2*B1 + n +1) lẻ và ngược lại
Khi n lẻ thì (2*B1 + n +1) chẵn.
Kết hợp với (*) ta thấy:
136 là tích của 2 thừa số khác tính chẵn lẻ: n và (2*B1 + n +1)
Trong khi 136 khi phân tích ra thừa số nguyên tố thì: 136 = 2*2*2*17 Tức là Khi phân tích 136 thành tích của 2 thừa số (1 chẵn, 1 lẻ) thì chỉ có thể phân tích thành (8*17).
Lưu ý rằng: ∀ n, B1 ∈ N ta luôn có n < (2*B1+n+1)
Vì thế n=8 và (2*B1+n+1) = 17 ==> B1=4 ==> B1+1=5
Vậy: Trang đầu tiên bị xé mất là trang số 5
Số trang bị xé mất là 8.
Kiểm tra lại: Tổng các số trang bị xé mất (8 trang) là
Sb = 5+6+7+8+9+10+11+12 = 68 (đúng).
================================================
BẠN NÀO THỰC SỰ MUỐN GIỎI TOÁN THÌ LIÊN HỆ VỚI TÔI NHÉ (h u n g v t 1 8 1 @ g m a i l . c o m). Nhà tôi gần SVĐ Mỹ Đình. TÔI KÈM CẶP, DẠY CÁC BẠN CÁCH TƯ DUY ĐỂ GIỎI TOÁN (từ lớp 3 - lớp 12). Tôi kg công tác trong ngành giáo dục nhưng là dân Chuyên toán Sư Phạm những năm 1986-1989, và đã từng giảng dạy chuyên môn cho các Tiến sỹ ngoại quốc. (Tôi đã nghỉ hưu nên có nhiều thời gian. Kinh tế tôi đủ sống nên tôi giúp các bạn miễn phí). CHỈ YÊU CẦU CÁC BẠN HỌC NGHIÊM TÚC.

Gợi ý bạn giải:
Ta biết Năng suất lao động = Khối lượng công việc chia cho Thời gian, và Thời gian = Khối lượng công việc chia cho Năng suất lao động.
Từ đó: Nếu gọi V là khối lượng công việc mà 3 người cùng làm, thì từ dữ kiện đã cho ta tính được Năng suất N1, N2, N3 (theo tuần) của 3 người theo V
==> Tính được Năng suất hàng tuần khi cả 3 người cũng làm công việc đó là N=(N1+N2+N3)
==> thời gian mà cả 3 người cùng làm để hoàn thành công việc là Tt = (V / N) tuần (Tt có nghĩa là T tính theo tuần).
==> Số giờ mà cả 3 người cùng làm để hoàn thành Công việc sẽ là Tg = (Tt*45) giờ (Tg có nghĩa T tính theo giờ).
Nếu bạn giải ra kết quả Tg=20 giờ là bạn đã làm đúng.
(Bạn cứ làm tuần tự đúng như hướng dẫn thì biến V sẽ tự triệt tiêu để cho ra các kết quả là con số như ta mong muốn).
Mình có thể giải chi tiết cho bạn, nhưng mình kg muốn bạn Copy và Paste lời giải mà kg hiểu gì. Như vậy giúp bạn mà hóa ra lại làm hại bạn.
================================================
BẠN NÀO THỰC SỰ MUỐN GIỎI TOÁN THÌ LIÊN HỆ VỚI MÌNH NHÉ (h u n g v t 1 8 1 @ g m a i l . c o m). Nhà mình gần SVĐ Mỹ Đình. MÌNH KÈM CẶP, DẠY CÁC BẠN CÁCH TƯ DUY ĐỂ GIỎI TOÁN (từ lớp 3 - lớp 12). Mình kg công tác trong ngành giáo dục nhưng là dân Chuyên toán Sư Phạm những năm 1986-1989, và đã từng giảng dạy chuyên môn cho các Tiến sỹ ngoại quốc. (Mình đã nghỉ hưu nên có nhiều thời gian. Kinh tế mình đủ sống nên mình giúp các bạn MIỄN PHÍ). CHỈ YÊU CẦU CÁC BẠN HỌC NGHIÊM TÚC.

\(\dfrac{\overline{abcabc}:1001}{\overline{defdef}:1001}=\dfrac{\overline{abc}}{\overline{def}}\)

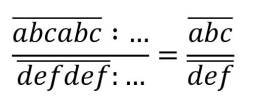
Trong 1 tháng có 12 ngày gây nhầm lẫn
Trong 1 năm có
12x12=144 ngày gây nhầm lẫn