Tìm a để đã thức (2x^3 - 4x^2 + 3x + a - 10) chia hết cho đa thức (x -2) có lời giải chỉ tiết ạ (mình cảm ơn ạ)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Xét ΔAMB và ΔAMC có
AM chung
MB=MC
AB=AC
Do đó: ΔAMB=ΔAMC
b: Ta có: \(\widehat{ABD}=\dfrac{\widehat{ABC}}{2}\)
\(\widehat{ACE}=\dfrac{\widehat{ACB}}{2}\)
mà \(\widehat{ABC}=\widehat{ACB}\)(ΔABC cân tại A)
nên \(\widehat{ABD}=\widehat{ACE}\)
Xét ΔABD và ΔACE có
\(\widehat{ABD}=\widehat{ACE}\)
AB=AC
\(\widehat{BAD}\) chung
Do đó: ΔABD=ΔACE
=>AD=AE

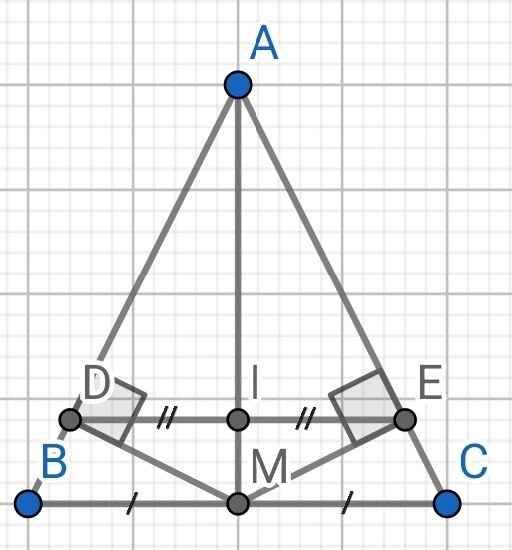
a) Do ∆ABC cân tại A (gt)
⇒ AB = AC
Do M là trung điểm của BC (gt)
⇒ MB = MC
Xét ∆ABM và ∆ACM có:
AB = AC (cmt)
AM là cạnh chung
MB = MC (gt)
⇒ ∆ABM = ∆ACM (c-c-c)
b) Do ∆ABC cân tại A (gt)
M là trung điểm của BC (gt)
⇒ AM là đường trung tuyến
⇒ AM cũng là đường phân giác
⇒ AM là tia phân giác của ∠DAE
⇒ ∠DAM = ∠EAM
Xét hai tam giác vuông: ∆ADM và ∆AEM có:
AM là cạnh chung
∠DAM = ∠EAM (cmt)
⇒ ∆ADM = ∆AEM (cạnh huyền - góc nhọn)
⇒ AD = AE (hai cạnh tương ứng)
⇒ ∆ADE cân tại A
c) ∆ADE cân tại A (cmt)
I là trung điểm của DE (gt)
⇒ AI là đường trung tuyến của ∆ADE
⇒ AI cũng là đường phân giác của ∆ADE
⇒ AI là tia phân giác của ∠DAE
Mà AM là tia phân giác của ∠DAE (cmt)
⇒ A, I, M thẳng hàng

a, Ta có : \(A\left(x\right)=-11x^5+4x-12x^{2^{ }}+11x^5+13x^2-7x+2\\ \Rightarrow A\left(x\right)=x^2-3x+2\)
Ta có: \(M\left(x\right)=A\left(x\right).B\left(x\right)\)
\(\Rightarrow M\left(x\right)=\left(x^2-3x+2\right).\left(x-1\right)\\\Rightarrow M\left(x\right)=x^3-x^2-3x^2+3x+2x-2\\ \Rightarrow M\left(x\right)=x^3-4x^2+5x-2. \)
Vậy...
b) Cho A(x) = 0
x² - 3x + 2 = 0
x² - x - 2x + 2 = 0
(x² - x) - (2x - 2) = 0
x(x - 1) - 2(x - 1) = 0
(x - 1)(x - 2) = 0
x - 1 = 0 hoặc x - 2 = 0
*) x - 1 = 0
x = 0 + 1
x = 1
*) x - 2 = 0
x = 0 + 2
x = 2
Vậy nghiệm của đa thức A(x) là x = 1; x = 2

a: Xét ΔABE vuông tại A và ΔDBE vuông tại D có
BE chung
\(\widehat{ABE}=\widehat{DBE}\)
Do đó: ΔABE=ΔDBE
b: ta có: ΔABE=ΔDBE
=>EA=ED
mà ED<EC(ΔEDC vuông tại E)
nên EA<EC

\(A⋮B\)
=>\(x^4+3x^3-3x^2-ax+b⋮x^2+3x+1\)
=>\(x^4+3x^3+x^2-4x^2-12x-4+\left(12-a\right)x+b+4⋮x^2+3x+1\)
=>12-a=0 và b+4=0
=>\(\left\{{}\begin{matrix}a=12\\b=-4\end{matrix}\right.\)

a: Sửa đề; MF vuông góc với AC tại F
Xét ΔBEM vuông tại E và ΔCFM vuông tại F có
BM=CM
\(\widehat{MBE}=\widehat{MCF}\)
Do đó: ΔBEM=ΔCFM
b: Ta có: ΔBEM=ΔCFM
=>ME=MF
=>M nằm trên đường trung trực của EF(1)
ta có: ΔBEM=ΔCFM
=>BE=CF
Ta có: AE+EB=AB
AF+FC=AC
mà BE=FC và AB=AC
nên AE=AF
=>A nằm trên đường trung trực của EF(2)
Từ (1),(2) suy ra AM là đường trung trực của EF
c: Xét ΔABC có \(\dfrac{AE}{AB}=\dfrac{AF}{AC}\)
nên EF//BC
d: Xét ΔABD vuông tại B và ΔACD vuông tại C có
AD chung
AB=AC
Do đó: ΔABD=ΔACD
=>DB=DC
=>D nằm trên đường trung trực của BC(3)
ta có: AB=AC
=>A nằm trên đường trung trực của BC(4)
ta có: MB=MC
=>M nằm trên đường trung trực của BC(5)
Từ (3),(4),(5) suy ra A,M,D thẳng hàng

Cho \(x=-4\), ta có \(-5f\left(-4\right)=0\) \(\Leftrightarrow f\left(-4\right)=0\)
Cho \(x=1\), ta có \(0=5f\left(-7\right)\) \(\Leftrightarrow f\left(-7\right)=0\)
Do đó \(-4,-7\) là 2 nghiệm của \(f\left(x\right)\). Đặt \(f\left(x\right)=\left(x+4\right)\left(x+7\right)g\left(x\right)\).
Khi đó điều kiện đề bài \(\Rightarrow\left(x-1\right)\left(x+4\right)\left(x+7\right)g\left(x\right)=\left(x+4\right)\left(x-4\right)\left(x-1\right)g\left(x-8\right)\)
Cho \(x=4\) thì ta có \(3.8.11g\left(4\right)=0\) \(\Leftrightarrow g\left(4\right)=0\)
Cho \(x=12\) thì ta có \(11.16.19.g\left(12\right)=16.8.11.g\left(4\right)=0\) (do \(g\left(4\right)=0\)) \(\Leftrightarrow g\left(12\right)=0\)
Vậy \(4,12\) là 2 nghiệm của \(g\left(x\right)\) \(\Rightarrow g\left(x\right)=\left(x-4\right)\left(x-12\right)h\left(x\right)\)
Vậy \(f\left(x\right)=\left(x+4\right)\left(x+7\right)\left(x-4\right)\left(x-12\right)h\left(x\right)\). Do đó 4 nghiệm của \(f\left(x\right)\) là \(-7,-4,4,12\)
\(2x^3-4x^2+3x+a-10=2x^3-4x^2+3x-6+a-4\)
\(=\left(2x^3-4x^2\right)+\left(3x-6\right)+a-4\)
\(=2x^2\left(x-2\right)+3\left(x-2\right)+a-4\)
\(\Rightarrow\left(2x^3-4x^2+3x+a-10\right):\left(x-2\right)\)
\(=\left[2x^2\left(x-2\right)+3\left(x-2\right)+a-4\right]:\left(x-2\right)\)
\(=2x^2+3+\dfrac{a-4}{x-2}\)
Để đa thức đã cho chia hết cho \(x-2\) thì \(a-4=0\)
\(\Rightarrow a=4\)