Bạn xem lời giải tại đây:

https://hoc24.vn/cau-hoi/cho-tam-giac-abc-can-tai-aduong-cao-ahve-he-vuong-goc-voi-ab-tai-egoi-ck-la-duong-cao-cua-tam-giac-abcchung-minh1-phan-ck21-phan-cb2-1-phan.8561726987074

a) 

b) Phương trình hoành độ giao điểm của hai đường thẳng đã cho:

-3x + 5 = 2x

⇔ 2x + 3x = 5

⇔ 5x = 5

⇔ x = 1 ⇒ y = 2.1 = 2

Vậy M(1; 2)

\(\Leftrightarrow x^2-4x+3>0\left(x\ne\pm5\right)\)

\(\Leftrightarrow\left[{}\begin{matrix}x< 1\\x>3\end{matrix}\right.\)

Lời giải:
ĐK: $25-x^2>0\Leftrightarrow -5< x< 5$
$\frac{x^2-4x+3}{\sqrt{25-x^2}}>0$

$\Leftrightarrow x^2-4x+3>0$ (do $\sqrt{25-x^2}>0$)

$\Leftrightarrow (x-1)(x-3)>0$

$\Leftrightarrow x>3$ hoặc $x<1$

Kết hợp với đkxđ suy ra $3< x< 5$ hoặc $-5< x< 1$

a.Ta có:
ˆAKC=ˆAHB=90o,ˆKAC=ˆBAH���^=���^=90�,���^=���^

→ΔAKC∼ΔAHB(g.g)→Δ���∼Δ���(�.�)

→AKAH=ACAB→����=����

→AKAC=AHAB→����=����

Mà ˆKAH=ˆBAC���^=���^

→ΔAKH∼ΔACB(c.g.c)→Δ���∼Δ���(�.�.�)

→KHBC=AKAC=cosˆKAC=cosA→����=����=cos⁡���^=cos⁡�

→HK=BC.cosA→��=��.cos⁡� 

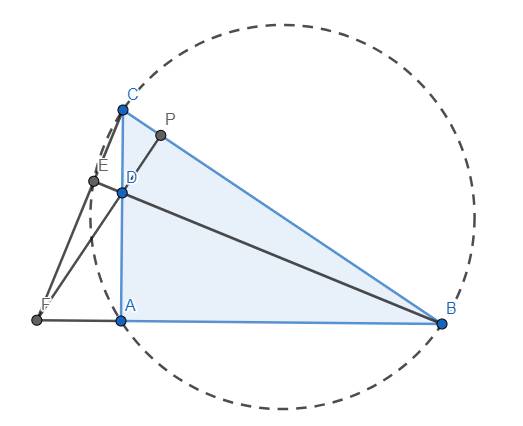
 a) Ta có \(\widehat{CEB}=\widehat{CAB}=90^o\) nên 4 điểm A, B, C, E cùng thuộc đường tròn đường kính BC.

 b) Kẻ \(FP\perp BC\) tại P. Ta thấy D là trực tâm tam giác FBC nên \(P\in DF\). Dễ thấy \(\Delta CDP~\Delta CBA\left(g.g\right)\) \(\Rightarrow\dfrac{CD}{CB}=\dfrac{CP}{CA}\) \(\Rightarrow CD.CA=CB.CP\)

CMTT, ta có \(BD.BE=BC.BP\)

Do đó \(CD.CA+BD.BE=CB.CP+BC.BP\) \(=BC\left(CP+BP\right)\) \(=BC^2\). Vậy đẳng thức được chứng minh.

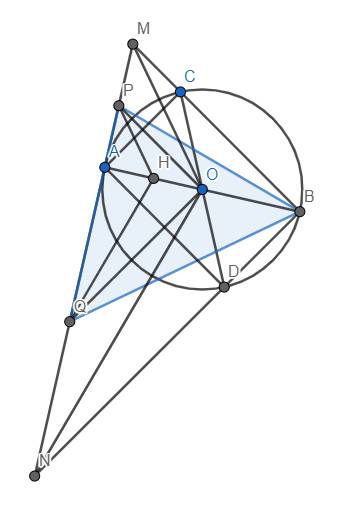
 a) Tam giác ABM vuông tại A có đường cao AC nên \(BC.BM=BA^2\). CMTT, \(BD.BN=BA^2\) nên \(BC.BM=BD.BN\Leftrightarrow\dfrac{BM}{BD}=\dfrac{BN}{BC}\). Từ đây dễ dàng suy ra \(\Delta BNM~\Delta BCD\left(c.g.c\right)\) (đpcm)

 b) Ta có OQ//BN, OP//BM, mà \(MB\perp NB\) nên suy ra \(OP\perp BN\), từ đó O là trực tâm tam giác BPN.\(\Rightarrow ON\perp BP\)

 Lại có \(QH\perp BP\) nên QH//ON.

Tam giác AON có Q là trung điểm AN, QH//ON nên H là trung điểm OA \(\Rightarrow AH=\dfrac{OA}{2}=\dfrac{R}{2}\) không đổi.