Tìm x, y thỏa mãn: \(2x^2+y^2-2xy+2x+1=0\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Giả sử ngược lại \(2^n-1\) là 1 số chính phương lẻ
Khi đó \(2^n-1=\left(2k+1\right)^2\) \(\left(k\inℕ^∗\right)\)
\(\Leftrightarrow2^n-1=4k^2+4k+1\)
\(\Leftrightarrow2^n=4k^2+4k+2\)
Nhận thấy VP chia hết cho 2 nhưng không chia hết cho 4
Mà n>1 nên 2n chia hết cho 4
=> vô lý => điều g/s sai
=> 2n - 1 không là 1 SCP

\(n^3-n=n\left(n^2-1\right)\) \(=n\left(n-1\right)\left(n+1\right)\)\(=\)\(\left(n-1\right)\times n\times\left(n+1\right)\)
Ta thấy: \(\left(n-1\right),n,\left(n+1\right)\)là 3 số tự nhiên liên tiếp
mà tích của 3 số tự nhiên liên tiếp luôn chia hết cho 6
nên \(n^3-n⋮6\)
n3 - n = n( n2 - 1 ) = n( n - 1 )( n + 1 )
Vì n, ( n - 1 ), ( n + 1 ) là 3 số nguyên liên tiếp nên sẽ có 1 số chia hết cho 2 và 1 số chia hết cho 3
mà 2.3 = 6 => n( n - 1 )( n + 1 ) chia hết cho 6
hay n3 - n chia hết cho 6 ( đpcm )

fuck mày trả lời đúng rồi nhưng mày không biết viết tiếng anh à ?

g, \(\frac{x+2}{98}+\frac{x+4}{96}=\frac{x+6}{94}+\frac{x+8}{92}\)
\(\Leftrightarrow\frac{x+2}{98}+1+\frac{x+4}{96}+1=\frac{x+6}{94}+1+\frac{x+8}{92}+1\)
\(\Leftrightarrow\frac{x+100}{98}+\frac{x+100}{96}-\frac{x+100}{94}-\frac{x+100}{92}=0\)
\(\Leftrightarrow\left(x+100\right)\left(\frac{1}{98}+\frac{1}{96}-\frac{1}{94}-\frac{1}{92}\ne0\right)=0\Leftrightarrow x=-100\)
e, \(\frac{1}{2}\left(x+1\right)+\frac{1}{4}\left(x+3\right)=3-\frac{1}{3}\left(x+2\right)\)
\(\Leftrightarrow\frac{x+1}{2}+\frac{x+3}{4}=3-\frac{x+2}{3}\)
\(\Leftrightarrow\frac{6x-6+3x+9}{12}=\frac{36-4x-8}{12}\)
\(\Rightarrow9x+3=28-4x\Leftrightarrow13x=25\Leftrightarrow x=\frac{25}{13}\)

\(7xy^5\left(x-1\right)-3x^2y^4\left(1-x\right)+5xy^3\left(x-1\right)\)
\(=7xy^5\left(x-1\right)+3x^2y^4\left(x-1\right)+6xy^3\left(x-1\right)\)
\(=\left(x-1\right)\left(7xy^5+3x^2y^4-6xy^3\right)=xy\left(x-1\right)\left(7y^4+3xy^3-6y^2\right)\)

2) \(\left(x+1\right)\left(x-4\right)\left(x+2\right)\left(x-8\right)+4x^2=0\)
\(\Leftrightarrow\left[\left(x+1\right)\left(x-8\right)\right]\left[\left(x-4\right)\left(x+2\right)\right]+4x^2=0\)
\(\Leftrightarrow\left(x^2-7x-8\right)\left(x^2-2x-8\right)+4x^2=0\)
Nếu x = 0 thì PT vô nghiệm
Nếu x khác 0, chia cả 2 vế cho x2 ta được:
\(PT\Leftrightarrow\left(x-\frac{8}{x}-7\right)\left(x-\frac{8}{x}-2\right)+4=0\)
Đặt \(x-\frac{8}{x}=b\) khi đó:
\(\left(b-7\right)\left(b-2\right)+4=0\)
\(\Leftrightarrow b^2-9b+14+4=0\)
\(\Leftrightarrow b^2-9b+18=0\)
\(\Leftrightarrow\left(b-3\right)\left(b-6\right)=0\Leftrightarrow\orbr{\begin{cases}b-3=0\\b-6=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}b=3\\b=6\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x-\frac{8}{x}=3\\x-\frac{8}{x}=6\end{cases}}\Leftrightarrow\orbr{\begin{cases}x^2-8=3x\\x^2-8=6x\end{cases}}\Leftrightarrow\orbr{\begin{cases}x^2-3x-8=0\\x^2-6x-8=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=\frac{3\pm\sqrt{41}}{2}\\x=3\pm\sqrt{17}\end{cases}}\)
Vậy ...
3) \(\left(x-2\right)\left(x-4\right)\left(x-5\right)\left(x-10\right)-54x^2=0\)
\(\Leftrightarrow\left[\left(x-2\right)\left(x-10\right)\right]\left[\left(x-4\right)\left(x-5\right)\right]-54x^2=0\)
\(\Leftrightarrow\left(x^2-12x+20\right)\left(x^2-9x+20\right)-54x^2=0\)
Nếu x = 0 thì PT vô nghiệm
Nếu x khác 0 thì chia cả 2 vế cho x2 ta được:
\(PT\Leftrightarrow\left(x+\frac{20}{x}-12\right)\left(x+\frac{20}{x}-9\right)-54=0\)
Đặt \(x+\frac{20}{x}=c\) nên khi đó:
\(\left(c-12\right)\left(c-9\right)-54=0\)
\(\Leftrightarrow c^2-21c+108-54=0\)
\(\Leftrightarrow c^2-21c+54=0\)
\(\Leftrightarrow\left(c-3\right)\left(c-18\right)=0\Leftrightarrow\orbr{\begin{cases}c-3=0\\c-18=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}c=3\\c=18\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x+\frac{20}{x}=3\\x+\frac{20}{x}=18\end{cases}}\Leftrightarrow\orbr{\begin{cases}x^2+20=3x\\x^2+20=18x\end{cases}}\Leftrightarrow\orbr{\begin{cases}x^2-3x+20=0\\x^2-18x+20=0\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}\left(x-\frac{3}{2}\right)^2=-\frac{71}{4}\left(ktm\right)\\x=9\pm\sqrt{61}\end{cases}}\)
Vậy ...

Cho \(x=\frac{b^2+c^2-a^2}{2ab},y=\frac{a^2-\left(b-c\right)^2}{\left(b+c\right)^2-a^2}\)
Tính giá trị của:
\(M=\frac{x+y}{1-xy}\)
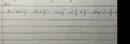
2x2 + y2 - 2xy + 2x + 1 = 0
<=> (x2 - 2xy + y2) + (x2 + 2x + 1) = 0
<=> (x - y)2 + (x + 1)2 = 0
<=> \(\hept{\begin{cases}x-y=0\\x+1=0\end{cases}}\Rightarrow\hept{\begin{cases}x=y\\x=-1\end{cases}}\Rightarrow x=y=-1\)
Vậy x = y = -1 là nghiệm phương trình
\(2x^2+y^2-2xy+2x+1=0\)
\(\Leftrightarrow\left(x^2-2xy+y^2\right)+\left(x^2+2x+1\right)=0\)
\(\Leftrightarrow\left(x-y\right)^2+\left(x+1\right)^2=0\)
Vì \(\left(x-y\right)^2\ge0\), \(\left(x+1\right)^2\ge0\forall x,y\)
\(\Rightarrow\left(x-y\right)^2+\left(x+1\right)^2\ge0\)
Dấu " = " xảy ra \(\Leftrightarrow\hept{\begin{cases}x-y=0\\x+1=0\end{cases}}\Leftrightarrow x=y=-1\)
Vậy nghiệm của phương trình là \(\left(x;y\right)=\left(-1;-1\right)\)