giải phương trình nghiệm nguyên:
x(y^2+1)+2y(x-2)=0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Là một biểu thức biểu diễn mối quan hệ của các biến số thông qua dấu bằng.

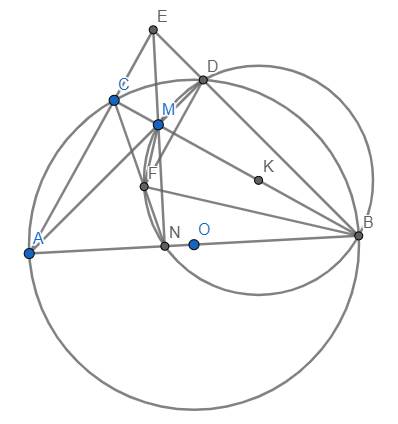
a) Tứ giác BDFN nội tiếp nên \(\widehat{CNA}=\widehat{BDF}\) (*)
Xét đường tròn (K), đường kính BM, ta có \(\widehat{MNB}=90^o\) hay \(MN\perp AB\) tại N (1)
Với lí do tương tự, ta có \(AD\perp EB,BC\perp EA\), do đó M là trực tâm của tam giác EAB \(\Rightarrow EM\perp AB\) (2)
Từ (1) và (2) \(\Rightarrow\) M, N, P thẳng hàng và đường thẳng này vuông góc với AB.
Từ đó suy ra tứ giác BECN nội tiếp (vì \(\widehat{ECB}=\widehat{ENB}=90^o\))
\(\Rightarrow\widehat{CNA}=\widehat{AEB}\) (**)
Từ (*) và (**), suy ra \(\widehat{BDF}=\widehat{BEA}\) \(\Rightarrow\) DF//AE (đpcm)
b) Tương tự như trên, ta có tứ giác AEDN nội tiếp \(\Rightarrow\widehat{BND}=\widehat{AEB}\), dẫn đến \(\Delta BDN~\Delta BAE\left(g.g\right)\) \(\Rightarrow\dfrac{BD}{BA}=\dfrac{BN}{BE}\Rightarrow BD.BE=BA.BN\) (3)
Tứ giác NBMD nội tiếp nên \(\widehat{ANM}=\widehat{ADB}\), dẫn đến \(\Delta AMN~\Delta ABD\left(g.g\right)\)
\(\Rightarrow\dfrac{AM}{AB}=\dfrac{AN}{AD}\Rightarrow AD.AM=AB.AN\) (4)
Cộng theo vế (3) và (4), thu được \(BD.BE+AM.AD=AB.BN+AB.AN=AB\left(BN+AN\right)=AB^2=4R^2\)không thay đổi. (đpcm)


\(2x^2+3xy+y^2+5x+3y=15\)
\(\Leftrightarrow y^2+3\left(x+1\right)y+2x^2+5x-15=0\)
\(\Delta=\left[3\left(x+1\right)\right]^2-4\left(2x^2+5x-15\right)\)
\(=9x^2+18x+9-8x^2-20x+60\)
\(=x^2-2x+69=\left(x-1\right)^2+68\ge68>0\) nên pt (*) luôn có nghiệm thực.
Do đó \(y=\dfrac{-3\left(x+1\right)\pm\sqrt{x^2-2x+69}}{2}\)
Vì y là số nguyên nên \(x^2-2x+69\) là số chính phương. Đặt \(x^2-2x+69=k^2\) \(\left(k\inℕ,k\ge9\right)\)
\(\Leftrightarrow\left(x-1\right)^2+68=k^2\)
\(\Leftrightarrow\left(k-x+1\right)\left(k+x-1\right)=68\)
Ta có bảng sau:
| \(k-x+1\) | 1 | 2 | 4 | 17 | 34 | 68 | -1 | -2 | -4 | -17 | -34 | -68 |
| \(k+x-1\) | 68 | 34 | 17 | 4 | 2 | 1 | -68 | -34 | -17 | -4 | -2 | -1 |
| \(k\) | \(\dfrac{69}{2}\) (loại) | 18 | \(\dfrac{21}{2}\) (loại) | \(\dfrac{21}{2}\) (loại) | 18 | \(\dfrac{69}{2}\)(loại) | \(-\dfrac{69}{2}\)(loại) | -18 | \(-\dfrac{21}{2}\)(loại) | \(-\dfrac{21}{2}\)(loại) | -18 | \(-\dfrac{69}{2}\)(loại) |
| \(x\) | 17 | -15 | -15 | 17 | ||||||||
| \(y\) | -18 hoặc -36 | 30 hoặc 12 | tương tự TH thứ 5 | tương tự TH thứ 2 |
Thử lại, ta thấy pt đã cho có các nghiệm nguyên sau:
(17; -18), (17; -36), (15; 30), (15; 12)

* Với dạng bài này, bạn giải bằng cách bình phương cả 2 vế nhé, nhớ đặt điều kiện xác định để phương trình có nghĩa(là để căn ko âm đấy) và đối chiếu x tìm được với ĐK.
a) \(\sqrt{ }\)16x = 8 (ĐKXĐ: x\(\ge\) 0)
\(\Leftrightarrow\) 16x =64
\(\Leftrightarrow\) x = 4 (thỏa mãn ĐKXĐ)
Vậy x=4 (đối với đề bài yêu cầu tìm x)
Vậy phương trình có nghiệm là x=4 (đối với đề bài yêu cầu giải phương trình). Cái này đề bài yêu cầu gì thì bạn KL theo cách mà mình nói nhé.
b) \(\sqrt{ }\)4x = \(\sqrt{ }\)5 (ĐKXĐ: x\(\ge\) 0)
\(\Leftrightarrow\) 4x = 5
\(\Leftrightarrow\) x =5/4 (thỏa mãn ĐKXĐ)
Vậy...
c) \(\sqrt{x-1}\) = 21 (ĐKXĐ: x\(\ge\) 1)
\(\Leftrightarrow\) x-1 = 441
\(\Leftrightarrow\) x = 442 (thỏa mãn ĐKXĐ)
Vậy...

Lời giải:
Áp dụng BĐT Cauchy-Schwarz:
$\frac{2}{ab}+\frac{3}{a^2+b^2}=\frac{1}{2ab}+\frac{1}{2ab}+\frac{1}{2ab}+\frac{1}{2ab}+\frac{1}{a^2+b^2}+\frac{1}{a^2+b^2}+\frac{1}{a^2+b^2}$
$\geq \frac{(1+1+1+1+1+1+1)^2}{2ab+2ab+2ab+2ab+a^2+b^2+a^2+b^2+a^2+b^2}=\frac{49}{8ab+3(a^2+b^2)}$
$=\frac{49}{3(a+b)^2+2ab}\geq \frac{49}{3(a+b)^2+\frac{(a+b)^2}{2}}=\frac{49}{3+\frac{1}{2}}=14$
Ta có đpcm
Dấu "=" xảy ra khi $a=b=\frac{1}{2}$

Lời giải:
Áp dụng BĐT AM-GM:
$2A=2x^2y^2(x^2+y^2)=xy.[2xy(x^2+y^2)]\leq \left(\frac{x+y}{2}\right)^2.\left(\frac{2xy+x^2+y^2}{2}\right)^2$
$\Leftrightarrow 2A\leq \frac{(x+y)^6}{16}=\frac{1}{16}$
$\Rightarrow A\leq \frac{1}{32}$
Vậy $A_{\max}=\frac{1}{32}$. Giá trị này đạt được khi $x=y=\frac{1}{2}$

a, Để đt (d) đi qua A thì tọa độ điểm A phải thỏa mãn phương trình đường thẳng (d)
Thay tọa độ điểm A vào phương trình đường thẳng (d) ta có:
2.(-2) + m - 3 = 3
-4 + m - 3 = 3
m = 3 + 3 + 4
m = 10
b, đt (d) cắt trục tung tại đểm có tọa độ bằng - 3 khi và chỉ khi:
2.0 + m - 3 = -3
m - 3 = - 3
m = 0

7\(x^2\) - 24y2 = 41
Nếu \(x\) ⋮ 3 ⇒ 7\(x^2\) - 24y2 ⋮ 3 ⇒ 41 ⋮ 3 (vô lý loại)
Nếu \(x\) không chia hết cho 3
⇒ \(x^2\) = 3k + 1(theo tính chất của số chính phương số chính phương chia 3 chỉ có thể dư 1 hoặc không dư)
Thay \(x^2\) = 3k + 1 vào biểu thức 7\(x^2\) - 24y2 ta có:
7.(3k + 1) - 24y2 = 41
⇒ 21k + 7 - 24y2 = 41
21k - 24y2 = 41 - 7
3.(7k - 8y2) = 34 ⇒ 34 ⋮ 3 (vô lý loại)
Vậy không có giá trị nguyên nào của \(x\) thỏa mãn phương trình hay phương trình đã cho không có nghiệm nguyên (đpcm)