Cho 5a2+2b2=11ab với a>b/5>0.Tìm A=(4a2-5b2)/(a2+3ab)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Xét ΔADB vuông tại D có DE là đường cao
nên \(AE\cdot AB=AD^2\left(1\right)\)
Xét ΔADC vuông tại D có DF là đường cao
nên \(AF\cdot AC=AD^2\left(2\right)\)
Từ (1) và (2) suy ra \(AE\cdot AB=AF\cdot AC\)
=>\(\dfrac{AE}{AC}=\dfrac{AF}{AB}\)
Xét ΔAEF vuông tại A và ΔACB vuông tại A có
\(\dfrac{AE}{AC}=\dfrac{AF}{AB}\)
Do đó: ΔAEF~ΔACB
b: TH1: AD là đường trung tuyến
ΔABC vuông tại A có AD là đường trung tuyến
nên AD=DB=DC
\(\dfrac{1}{DB^2}+\dfrac{1}{DC^2}=\dfrac{1}{DA^2}+\dfrac{1}{DA^2}=\dfrac{2}{DA^2}\)
=>Đúng với GT

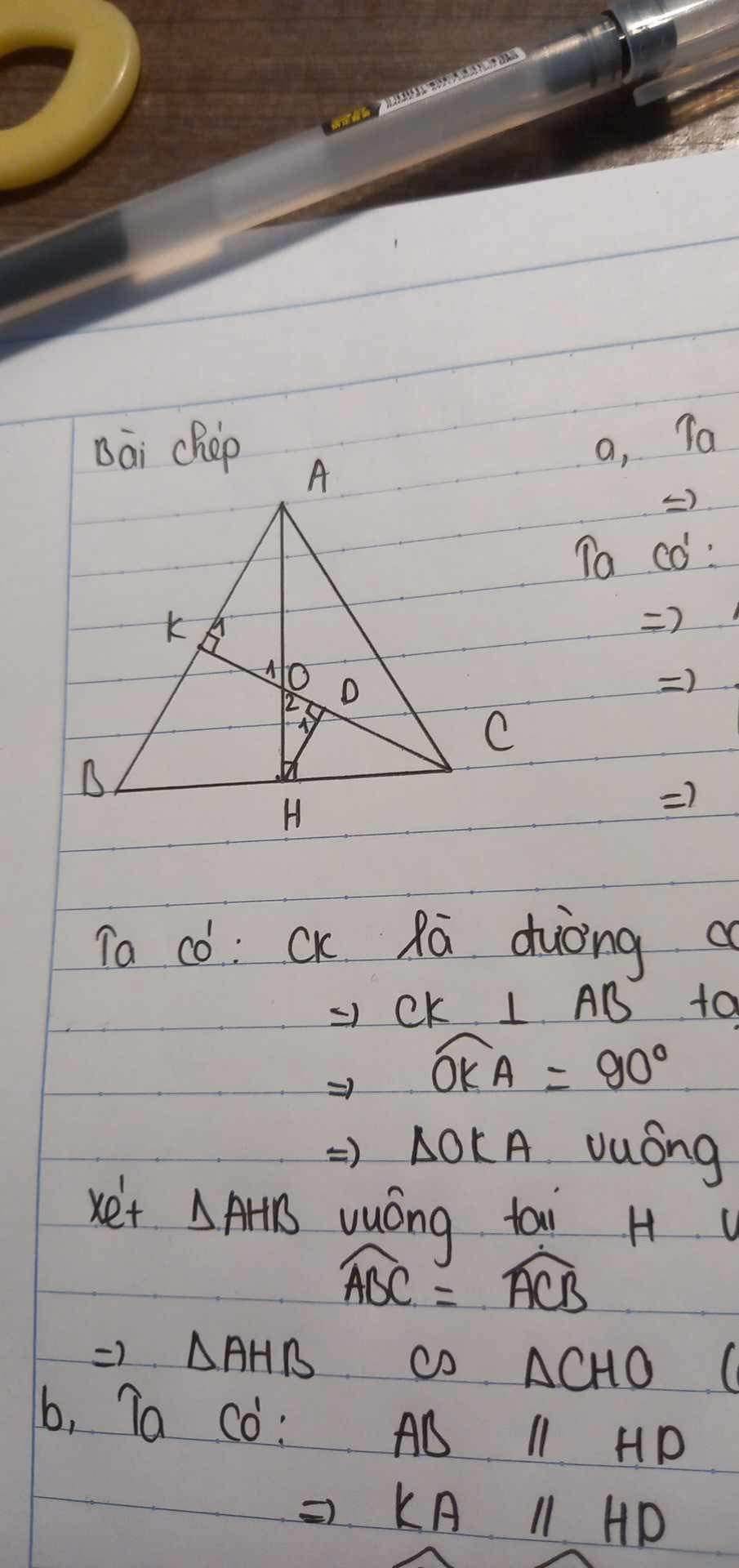
Đề bài cho tam giác ABC cân tại A đúng không em? Chỉ như vậy thì BK=2HD thôi
Ta có: H là trung điểm BC
\(BK||HD\) (cùng vuông góc CK)
\(\Rightarrow\) HD là đường trung bình tam giác BCK
\(\Rightarrow HD=\dfrac{1}{2}BK\Rightarrow BK=2HD\)

\(\dfrac{77}{25}\) là phân số tối giản rồi, không thể rút gọn được nữa bạn nhé.

a) Sửa: \(\dfrac{x-2}{x+2}+\dfrac{x}{2-x}+\dfrac{8}{x^2-4}\left(x\ne\pm2\right)\)
\(=\dfrac{\left(x-2\right)^2}{\left(x-2\right)\left(x+2\right)}-\dfrac{x}{x-2}+\dfrac{8}{\left(x-2\right)\left(x+2\right)}\)
\(=\dfrac{x^2-4x+4+8}{\left(x+2\right)\left(x-2\right)}-\dfrac{x\left(x+2\right)}{\left(x-2\right)\left(x+2\right)}\)
\(=\dfrac{x^2-4x+12-x^2-2x}{\left(x+2\right)\left(x-2\right)}\)
\(=\dfrac{-6x+12}{\left(x+2\right)\left(x-2\right)}\)
\(=\dfrac{-6\left(x-2\right)}{\left(x+2\right)\left(x-2\right)}\)
\(=\dfrac{-6}{x+2}\)
b) \(\dfrac{x}{x-2}+\dfrac{2-x}{x+2}+\dfrac{12-10x}{x^2-4}\left(x\ne\pm2\right)\)
\(=\dfrac{x\left(x+2\right)}{\left(x+2\right)\left(x+2\right)}-\dfrac{x-2}{x+2}+\dfrac{12-10x}{\left(x+2\right)\left(x-2\right)}\)
\(=\dfrac{x^2+2x+12-10x}{\left(x+2\right)\left(x-2\right)}-\dfrac{\left(x-2\right)^2}{\left(x+2\right)\left(x+2\right)}\)
\(=\dfrac{x^2-8x+12-x^2+4x-4}{\left(x+2\right)\left(x-2\right)}\)
\(=\dfrac{-4x+8}{\left(x+2\right)\left(x-2\right)}\)
\(=\dfrac{-4\left(x+2\right)}{\left(x+2\right)\left(x-2\right)}\)
\(=\dfrac{-4}{x-2}\)
c) \(C=\dfrac{2x}{x+3}+\dfrac{2}{x-3}+\dfrac{x^2-x+6}{9-x^2}\left(x\ne\pm3\right)\)
\(C=\dfrac{2x}{x+3}+\dfrac{2}{x-3}-\dfrac{x^2-x+6}{x^2-9}\)
\(C=\dfrac{2x\left(x-3\right)}{\left(x+3\right)\left(x-3\right)}+\dfrac{2\left(x+3\right)}{\left(x+3\right)\left(x-3\right)}-\dfrac{x^2-x+6}{\left(x+3\right)\left(x-3\right)}\)
\(C=\dfrac{2x^2-6x+2x+6-x^2+x-6}{\left(x+3\right)\left(x-3\right)}\)
\(C=\dfrac{x^2-3x}{\left(x+3\right)\left(x-3\right)}\)
\(C=\dfrac{x\left(x-3\right)}{\left(x+3\right)\left(x-3\right)}\)
\(C=\dfrac{x}{x+3}\)

\(\Leftrightarrow x\left(x+1\right)=y^2\)
+ Nếu \(y=0\)
\(\Rightarrow x\left(x+1\right)=0\Rightarrow\left[{}\begin{matrix}x=0\\x+1=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=0\\x=-1\end{matrix}\right.\)
+ Nếu \(y\ne0\)
\(\Rightarrow\left\{{}\begin{matrix}x=y^m\\x+1=y^n\end{matrix}\right.\)
\(\Rightarrow x\left(x+1\right)=y^m.y^n=y^{m+n}=y^2\Rightarrow m+n=2\) (1)
Ta có
\(y^n-y^m=\left(x+1\right)-x=1\)
\(\Leftrightarrow y^n\left(1-y^{m-n}\right)=1.1\)
\(\Rightarrow\left\{{}\begin{matrix}y^n=1\\y^{m-n}=0\end{matrix}\right.\) (2)
Kết hợp (1) và (2)
\(\Rightarrow\left\{{}\begin{matrix}y^n=1\\y^{m-n}=0\\m+n=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}n=0\\y=0\\m=2\end{matrix}\right.\) mâu thuẫn với đk \(y\ne0\)
\(\Rightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}x=0\\x=-1\end{matrix}\right.\\y=0\end{matrix}\right.\)

Ta thấy: \(2024\equiv1\) (\(mod\) \(2023\))
\(20242024\equiv1909\) (\(mod\) \(2023\))
...
\(2024...2024:2023\) dư một số nào đó là một trong các số từ \(1\) đến \(2022\) (\(2023\) số).
* Xét \(2024\) số: \(2024;20242024;...;20242024...2024\) (Gồm \(2024\) bộ số \(2024\))
+ Lấy \(2024\) số trên chia cho \(2023\), ta có \(2024\) số dư từ \(0\) đến \(2022\).
\(\Rightarrow\) Tồn tại hai số chia cho \(2023\) có cùng số dư.
Giả sử hai số đó là \(a=2024...2024\) (\(i\) bộ số \(2024\)) và \(b=2024...2024\) (\(j\) bộ số \(2024\)) \(\left(1\le i\le j\le2024\right)\)
+ \(a-b=2024...2024\cdot10^{4i}\) (\(j-i\) bộ số \(2024\)) chia hết cho \(2023\)
+ \(ƯCLN\left(10^{4i};2023\right)=1\)
\(\Rightarrow2024...2024\) (\(j-i\) bộ số \(2024\)) chia hết cho \(2023\) \(\left(đpcm\right)\).
Ta có: \(5a^2+2b^2=11ab\)
\(\Leftrightarrow5a^2-11ab+2b^2=0\)
\(\Leftrightarrow5a^2-10ab-ab+2b^2=0\)
\(\Leftrightarrow5a\left(a-2b\right)-b\left(a-2b\right)=0\)
\(\Leftrightarrow\left(a-2b\right)\left(5a-b\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}a-2b=0\\5a-b=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}a=2b\\5a=b\end{matrix}\right.\) (1)
Lại có: \(a>\dfrac{b}{5}>0\Rightarrow5a>b\) (2)
Từ (1) và (2) \(\Rightarrow a=2b\)
Thay \(a=2b\) vào \(A\), ta được:
\(A=\dfrac{4\left(2b\right)^2-5b^2}{\left(2b\right)^2+3\cdot2b\cdot b}=\dfrac{16b^2-5b^2}{4b^2+6b^2}=\dfrac{11b^2}{10b^2}=\dfrac{11}{10}\)
Vậy \(A=\dfrac{11}{10}\) là giá trị cần tìm.