Lời giải:

$7x^2-24y^2=41$

$\Rightarrow 7x^2=41+24y^2\equiv 41\equiv 2\pmod 3(1)$
Nếu $x$ nguyên thì $x^2$ là scp. Ta biết 1 scp khi chia 3 dư $0,1$

$\Rightarrow x^2\equiv 0,1\pmod 3$

$\Rightarrow 7x^2\equiv 0, 7\equiv 0,1\pmod 3$
Nghĩa là $7x^2$ chia 3 dư $0$ hoặc $1$ (2)

$(1); (2)$ mâu thuẫn nhau nên pt không có nghiệm nguyên.

Lời giải:

$7x^2-24y^2=41$

$\Rightarrow 7x^2=41+24y^2\equiv 41\equiv 2\pmod 3(1)$
Nếu $x$ nguyên thì $x^2$ là scp. Ta biết 1 scp khi chia 3 dư $0,1$

$\Rightarrow x^2\equiv 0,1\pmod 3$

$\Rightarrow 7x^2\equiv 0, 7\equiv 0,1\pmod 3$
Nghĩa là $7x^2$ chia 3 dư $0$ hoặc $1$ (2)

$(1); (2)$ mâu thuẫn nhau nên pt không có nghiệm nguyên.

 Cách khác (xét theo mod 8): Giả sử tồn tại 2 số nguyên x, y thỏa mãn \(7x^2-24y^2=41\) 

\(\Leftrightarrow7x^2-24y^2=48-7\)

\(\Leftrightarrow7\left(x^2+1\right)=24\left(y^2+2\right)\) (*)

 Do \(\left(7,24\right)=1\) nên từ (*), ta có \(x^2+1⋮24\) \(\Rightarrow x^2+1⋮8\)

 Từ đó x phải là số lẻ. Nhưng nếu như vậy thì \(x^2\equiv1\left[8\right]\) dẫn đến \(x^2+1\equiv2\left[8\right]\), vô lí.

 Vậy điều giả sử là sai \(\Rightarrow\) pt đã cho không có nghiệm nguyên.

Lời giải:
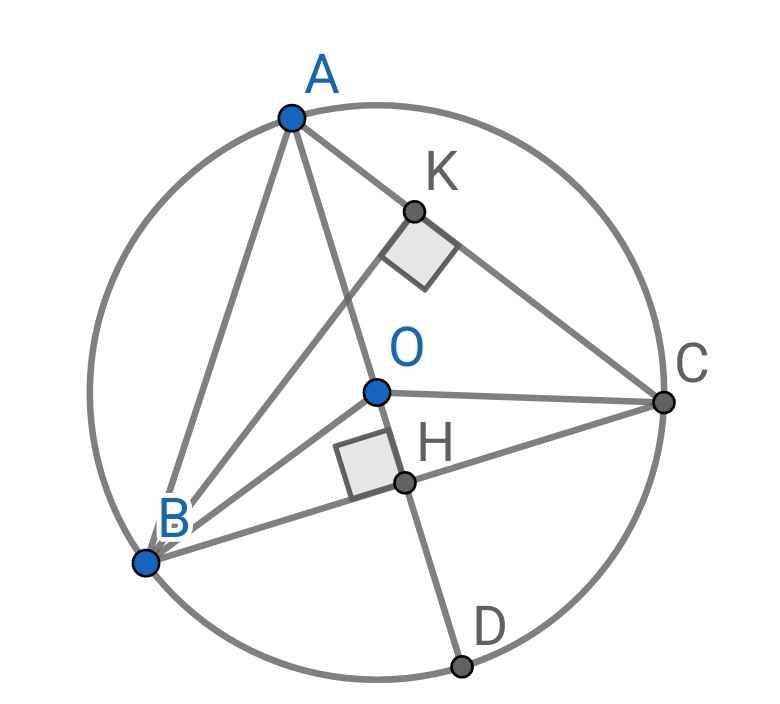
1. Vì $MA, MB$ là tiếp tuyến của $(O)$ nên $MA\perp OA, MB\perp OB$.

Khi đó $\widehat{MAO}=\widehat{MBO}=90^0$

Tứ giác $MAOB$ có tổng 2 góc đối nhau $\widehat{MAO}+\widehat{MBO}=90^0+90^0=180^0$

$\Rightarrow MAOB$ là tứ giác nội tiếp.

$\Rightarrow M,A,O,B$ cùng thuộc 1 đường tròn.

2.

Có: $MA=MB, OA=OB$ nên $MO$ là trung trực của $AB$

$\Rightarrow MO\perp AB$ tại $C$.

Xét tam giác $MOB$ vuông tại $B$ có đường cao $BC$. Áp dụng hệ thức lượng trong tam giác vuông thì:

$MC.MO=MB^2(1)$

Xét tam giác $MQB$ và $MBD$ có:

$\widehat{M}$ chung

$\widehat{MBQ}=\widehat{MDB}$ (góc tạo bởi tiếp tuyến và dây cung bằng góc nội tiếp chắn cung đó)

$\Rightarrow \triangle MQB\sim \triangle MBD$ (g.g)

$\Rightarrow \frac{MQ}{MB}=\frac{MB}{MD}$

$\Rightarrow MQ.MD=MB^2(2)$

Từ $(1); (2)\Rightarrow MQ.MD=MC.MO$ 

Hình vẽ:

Lời giải:

$2020\equiv 1\pmod 3\Rightarrow 2020x^3\equiv x^3\pmod 3$

$2021\equiv -1\pmod 3\Rightarrow 2021x\equiv -x\pmod 3$
$\Rightarrow 2020x^3+2021x\equiv x^3-x\pmod 3$
Mà $x^3-x=x(x^2-1)=x(x-1)(x+1)$ là tích 3 số nguyên liên tiếp nên $x^3-x\equiv 0\pmod 3$

$\Rightarrow 2020x^3+2021x\equiv 0\pmod 3(*)$

Mặt khác:
$y^{2022}=(y^{1011})^2$ là scp nên $y^{2022}\equiv 0,1\pmod 3$

$2023\equiv 1\pmod 3$

$\Rightarrow y^{2022}+2023\equiv 1,2\pmod 3(**)$

Từ $(*); (**)\Rightarrow 2020x^3+2021x\neq y^{2022}+2023$ với mọi $x,y$ nguyên.

Do đó không tồn tại $x,y$ thỏa đề.

Lời giải:

$2020\equiv 1\pmod 3\Rightarrow 2020x^3\equiv x^3\pmod 3$

$2021\equiv -1\pmod 3\Rightarrow 2021x\equiv -x\pmod 3$
$\Rightarrow 2020x^3+2021x\equiv x^3-x\pmod 3$
Mà $x^3-x=x(x^2-1)=x(x-1)(x+1)$ là tích 3 số nguyên liên tiếp nên $x^3-x\equiv 0\pmod 3$

$\Rightarrow 2020x^3+2021x\equiv 0\pmod 3(*)$

Mặt khác:
$y^{2022}=(y^{1011})^2$ là scp nên $y^{2022}\equiv 0,1\pmod 3$

$2023\equiv 1\pmod 3$

$\Rightarrow y^{2022}+2023\equiv 1,2\pmod 3(**)$

Từ $(*); (**)\Rightarrow 2020x^3+2021x\neq y^{2022}+2023$ với mọi $x,y$ nguyên.

Do đó không tồn tại $x,y$ thỏa đề.

Goi số học sinh đạt giải cao là \(x\) (học sinh)

Theo bài ra ta có: 3\(x\) + 7 = 4\(x\) - 2

                              4\(x\) - 3\(x\) = 7 + 2

                                  \(x\)      = 9

Vậy số học sinh đạt giải cao là 9 học sinh.

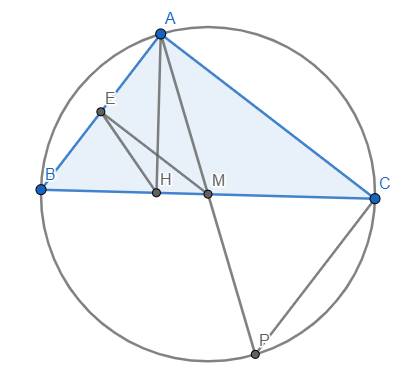
a) Gọi P là giao điểm của AM với (O). Tam giác ABH và APC có:

\(\widehat{BAH}=\widehat{PAC}\left(gt\right)\) và \(\widehat{ABH}=\widehat{APC}\) (góc nội tiếp cùng chắn cung AC)

 \(\Rightarrow\Delta ABH~\Delta APC\left(g.g\right)\) \(\Rightarrow\widehat{AHB}=\widehat{ACP}\).

 Mà \(\widehat{AHB}=90^o\Rightarrow\widehat{ACP}=90^o\) . Suy ra M nằm trên đường kính AP của (O).

 Mặt khác, M lại là trung điểm của dây BC của (O), do đó nếu dây BC không phải là đường kính của (O) thì phải có \(AP\perp BC\) , điều này không chắc chắn đúng. Do đó để đảm bảo M là trung điểm BC thì BC phải là đường kính của (O).

 \(\Rightarrow\) M là tâm của (O). Từ đó \(\widehat{MBA}=\widehat{MAB}\) 

Trong tam giác HAB vuông tại H có trung tuyến HE nên \(EH=EA=EB=\dfrac{AB}{2}\), do đó \(\widehat{ABM}=\widehat{EHB}\). 

 Từ đó suy ra \(\widehat{MAB}=\widehat{EHB}\) \(\Rightarrow\) Tứ giác AMHE nội tiếp (đpcm)

b) Từ câu a), ta có BC là đường kính của (O) nên suy ra đpcm.

Ta có: \(4x^2-2xy-2x=y-20\)

\(\Leftrightarrow y+2xy=4x^2-2x+20\)

\(\Leftrightarrow y\cdot\left(2x+1\right)=4x^2-2x+20\)

\(\Leftrightarrow y=\dfrac{4x^2-2x+20}{2x+1}\)

\(\Leftrightarrow y=\dfrac{4x^2+2x-4x+20}{2x+1}\)

\(\Leftrightarrow y=\dfrac{2x\left(2x+1\right)-4x-2+22}{2x+1}\)

\(\Leftrightarrow y=2x+\dfrac{-2\left(2x+1\right)+22}{2x+1}\)

\(\Leftrightarrow y=2x-2+\dfrac{22}{2x+1}\)

Để x,y ∈ Z thì \(\dfrac{22}{2x+1}\) có giá trị nguyên 

\(\Rightarrow2x+1\inƯ\left(22\right)=\left\{1;-1;2;-2;11;-11;22;-22\right\}\)

Mà nếu x nguyên thì \(2x+1\) luôn là số lẻ 

\(\Rightarrow2x+1\in\left\{1;-1;11;-11\right\}\)

\(\Rightarrow x\in\left\{0;-1;5;-6\right\}\)

Ta tìm được các số y tương ứng là:

\(x=0\Rightarrow y=20\)

\(x=-1\Rightarrow y=-26\)

\(x=5\Rightarrow y=10\)

\(x=-6\Rightarrow y=-16\)

Vậy các cặp x,y thỏa là: \(\left(0;20\right);\left(-1;-26\right);\left(5;10\right);\left(-6;-16\right)\)

 a) Ta có:

OB = OC (bán kính)

⇒ O nằm trên đường trung trực của BC (1)

Do ∆ABC cân tại A (gt)

AH là đường cao (gt)

⇒ AH cũng là đường trung trực của ∆ABC

⇒ AH là đường trung trực của BC (2)

Từ (1) và (2) suy ra O ∈ AH

⇒ O ∈ AD

Vậy AD là đường kính của (O)

b) Sửa đề: Tính độ dài các đường cao AH, BK của ∆ABC

Do AH là đường trung trực của BC (cmt)

⇒ H là trung điểm của BC

⇒ CH = BC : 2

= 12 : 2

= 6 (cm)

∆AHC vuông tại H

⇒ AC² = AH² + CH² (Pytago)

⇒ AH² = AC² - CH²

= 10² - 6²

= 64

⇒ AH = 8 (cm)

⇒ sinACH = AH/AC

= 4/5

⇒ ACH ≈ 53⁰

⇒ BCK ≈ 53⁰

∆BCK vuông tại K

⇒ sinBCK = BK/BC

⇒ BK = BC.sinBCK

= 10.sin53⁰

≈ 8 (cm)