cho 1 hình hộp chữ nhật có ba kích thước là 4,x và x+2(x lớn hơn 0).biểu thức biểu thị thể tích của hình hộp chữa nhật là biểu thức nào ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Xét ΔBAE vuông tại A và ΔBDE vuông tại D có
BE chung
\(\widehat{ABE}=\widehat{DBE}\)
Do đó: ΔBAE=ΔBDE
=>BA=BD
=>ΔBAD cân tại B
ΔBAE=ΔBDE
=>EA=ED
=>E nằm trên đường trung trực của AD(1)
ta có: BA=BD
=>B nằm trên đường trung trực của AD(2)
Từ (1),(2) suy ra BE là đường trung trực của AD
b: AE=ED
mà ED<EC(ΔEDC vuông tại D)
nên EA<EC

1: Xét ΔAND và ΔAME có
AN=AM
\(\widehat{NAD}=\widehat{MAE}\)
AD=AE
Do đó: ΔAND=ΔAME
2: Ta có: ΔAND=ΔAME
=>\(\widehat{AND}=\widehat{AME}\)
=>ME//ND
=>MF//DP
Xét ΔBMF và ΔBPD có
\(\widehat{BMF}=\widehat{BPD}\)(MF//DP)
BM=BP
\(\widehat{MBF}=\widehat{PBD}\)(hai góc đối đỉnh)
Do đó: ΔBMF=ΔBPD
=>BD=BF
=>B là trung điểm của DF

em nghĩ là : d - 15 á chị
vì câu này em phân tích như này ạ
13 - 1 =
12 +
Vậy câu tr
d) 15
em cũng ko biết đúng hay sai nhữa vì em mới học lớp 4 à !

\(\dfrac{1}{6}\) + \(\dfrac{2}{7}\) = \(\dfrac{7}{42}\) + \(\dfrac{12}{42}\) = \(\dfrac{19}{42}\)
Chọn c \(\dfrac{19}{42}\)

a: Ta có: \(MQ=QN=\dfrac{MN}{2}\)
\(MK=KP=\dfrac{MP}{2}\)
mà MN=MP
nên MQ=QN=MK=KP
Xét ΔMKN và ΔMQP có
MK=MQ
\(\widehat{KMN}\) chung
MN=MP
Do đó: ΔMKN=ΔMQP
b: Xét ΔQNP và ΔKPN có
QN=KP
QP=KN
NP chung
Do đó: ΔQNP=ΔKPN
=>\(\widehat{QPN}=\widehat{KNP}\)
=>\(\widehat{HNP}=\widehat{HPN}\)
=>ΔHNP cân tại H

a: Đặt a/b=c/d=k
=>\(a=bk;c=dk\)
\(\left(\dfrac{a-b}{c-d}\right)^2=\left(\dfrac{bk-b}{dk-d}\right)^2=\left(\dfrac{b\left(k-1\right)}{d\left(k-1\right)}\right)^2=\left(\dfrac{b}{d}\right)^2\)
\(\dfrac{ab}{cd}=\dfrac{bk\cdot b}{dk\cdot k}=\dfrac{b^2\cdot k}{d^2\cdot k}=\dfrac{b^2}{d^2}\)
Do đó: \(\left(\dfrac{a-b}{c-d}\right)^2=\dfrac{ab}{cd}\)
b: \(\left(\dfrac{a+b}{c+d}\right)^3=\left(\dfrac{bk+b}{dk+d}\right)^3=\left(\dfrac{b\left(k+1\right)}{d\left(k+1\right)}\right)^3=\left(\dfrac{b}{d}\right)^3\)
\(\dfrac{a^3-b^3}{c^3-d^3}=\dfrac{b^3k^3-b^3}{d^3k^3-d^3}=\dfrac{b^3\left(k^3-1\right)}{d^3\left(k^3-1\right)}=\dfrac{b^3}{d^3}\)
Do đó: \(\left(\dfrac{a+b}{c+d}\right)^3=\dfrac{a^3-b^3}{c^3-d^3}\)
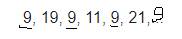
cíu mik với
Công thức biểu thị thể tích hình chữ nhật là:
4.\(x\)(\(x\) + 2) = 4\(x^2\) + 8\(x\)
Kết luận:
Công thức biểu thị thể tích hình chữ nhật là: 4\(x^2\) + 8\(x\)