 Mọi người giải giúp em bài 2,4,5 và câu b bài 6 ạ em đang cần gấp gấp lắm ạ mong mn giúp em
Mọi người giải giúp em bài 2,4,5 và câu b bài 6 ạ em đang cần gấp gấp lắm ạ mong mn giúp em
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

9: \(\left(\dfrac{2}{3}\right)^3-4\cdot\left(-1\dfrac{3}{4}\right)^2+\left(-\dfrac{2}{3}\right)^3\)
\(=\dfrac{8}{27}-4\cdot\left(\dfrac{7}{4}\right)^2-\dfrac{8}{27}\)
\(=-4\cdot\dfrac{49}{16}=-\dfrac{49}{4}\)
10: \(\left(-\dfrac{1}{3}\right)^{-1}-\left(-\dfrac{6}{7}\right)^0+\left(\dfrac{1}{2}\right)^2:2\)
\(=-3-1+\dfrac{1}{4}:2=-4+\dfrac{1}{8}=-\dfrac{31}{8}\)
11: \(25\cdot\left(-\dfrac{1}{5}\right)^2+\dfrac{1}{5}-9\cdot\left(-\dfrac{1}{9}\right)^2+\dfrac{1^{20}}{9}\)
\(=25\cdot\dfrac{1}{25}+\dfrac{1}{5}-9\cdot\dfrac{1}{81}+\dfrac{1}{9}\)
\(=\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{9}+\dfrac{1}{9}=\dfrac{2}{5}\)
12: \(\left(-\dfrac{1}{3}\right)^2+\left(-\dfrac{1}{4}\right)^3\cdot64+\left(-\dfrac{2015}{2016}\right)^0\)
\(=\dfrac{1}{9}+\dfrac{-1}{64}\cdot64+1\)
\(=\dfrac{1}{9}\)
13: \(\dfrac{1}{3}-\dfrac{1}{3}:\left(-\dfrac{2}{3}\right)^2+\left(-3\right)^3\cdot\left(7\dfrac{7}{9}-9\dfrac{2}{3}\right)\)
\(=\dfrac{1}{3}-\dfrac{1}{3}:\dfrac{4}{9}+\left(-27\right)\left(-2+\dfrac{7}{9}-\dfrac{2}{3}\right)\)
\(=\dfrac{1}{3}-\dfrac{1}{3}\cdot\dfrac{9}{4}+\left(-27\right)\cdot\left(-2+\dfrac{1}{9}\right)\)
\(=\dfrac{1}{3}-\dfrac{3}{4}+\left(-27\right)\cdot\dfrac{-17}{9}\)
\(=\dfrac{-5}{12}+51=\dfrac{607}{12}\)

Ta thấy \(N=n^4-n^2-2n-1\)
\(N=\left(n^2\right)^2-\left(n+1\right)^2\)
\(N=\left(n^2+n+1\right)\left(n^2-n-1\right)\)
Với \(n\inℕ\) thì \(n^2+n+1>n^2-n-1\) nên để N là SNT thì:
\(n^2-n-1=1\) (1) và \(n^2+n+1\) là SNT.
(1) \(\Leftrightarrow n^2-n-2=0\)
\(\Leftrightarrow n^2+n-2n-2=0\)
\(\Leftrightarrow n\left(n+1\right)-2\left(n+1\right)=0\)
\(\Leftrightarrow\left(n+1\right)\left(n-2\right)=0\)
\(\Leftrightarrow n=2\) (do n là số tự nhiên)
Khi đó \(n^2+n+1=2^2+2+1=7\) là SNT -> Thỏa mãn.
Vậy \(n=2\)

a: ΔABC cân tại A
=>\(\widehat{ABC}=\widehat{ACB}=\dfrac{180^0-45^0}{2}=67,5^0\)
Xét ΔABC có \(\widehat{ABC}=\widehat{ACB}>\widehat{BAC}\)
mà AC,AB,BC lần lượt là cạnh đối diện của các góc ABC,ACB,BAC
nên AC=AB>BC
b: Xét ΔDBC và ΔECB có
DB=EC
\(\widehat{DBC}=\widehat{ECB}\)
BC chung
Do đó: ΔDBC=ΔECB
=>\(\widehat{BDC}=\widehat{CEB}\)
c: D nằm trên đường trung trực của AC
=>DA=DC
Xét ΔDAC có DA=DC và \(\widehat{DAC}=45^0\)
nên ΔDAC vuông cân tại D
=>\(\widehat{ADC}=90^0\)
=>CD\(\perp\)AB
=>\(\widehat{CDB}=\widehat{CEB}=90^0\)
=>BE\(\perp\)AC
ΔABC cân tại A
mà AM là đường trung tuyến
nên AM\(\perp\)BC
Xét ΔABC có
AM,BE,CD là các đường cao
Do đó: AM,BE,CD đồng quy

a: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC
HA chung
Do đó: ΔAHB=ΔAHC
=>HB=HC
ΔAHB=ΔAHC
=>\(\widehat{BAH}=\widehat{CAH}\)
=>AH là phân giác của góc BAC
b: Xét ΔBHA vuông tại H và ΔBHD vuông tại H có
BH chung
HA=HD
Do đó: ΔBHA=ΔBHD
=>BA=BD
=>ΔBAD cân tại B
c: Ta có: \(\widehat{BDA}=\widehat{BAD}\)(ΔBAD cân tại B)
\(\widehat{BAD}=\widehat{CAH}\)(cmt)
Do đó: \(\widehat{BDA}=\widehat{DAC}\)
=>BD//AC

Gọi A là biến cố "Số ghi trên thẻ là số chia 6 dư 2"
=>A={2;8;14;20;26}
=>n(A)=5
\(P_A=\dfrac{5}{30}=\dfrac{1}{6}\)

1; (\(\dfrac{3}{4}\))2. 42 - (\(\dfrac{1}{2}\))2 : 2 - 2\(\dfrac{3}{4}\)
= \(\dfrac{3^2}{4^2}\).42 - \(\dfrac{1}{4}\) : 2 - 2\(\dfrac{3}{4}\)
= 9 - \(\dfrac{1}{8}\) - \(\dfrac{11}{4}\)
= \(\dfrac{72}{8}\) - \(\dfrac{1}{8}-\dfrac{22}{8}\)
= \(\dfrac{71}{8}\) - \(\dfrac{22}{8}\)
= \(\dfrac{49}{8}\)
2; (\(\dfrac{3}{5}\))2.52 - (2\(\dfrac{1}{4}\))3 : (\(\dfrac{3}{4}\))3 - 3
= \(\dfrac{9}{5^2}\).52 - (\(\dfrac{9}{4}\))3 : (\(\dfrac{3}{4}\))3 - 3
= 9 - (\(\dfrac{9}{4}\) : \(\dfrac{3}{4}\))3 - 3
= 9 - 33 - 3
= 9 - 27 - 3
= 9 - (27 + 3)
= 9 - 30
= - 21

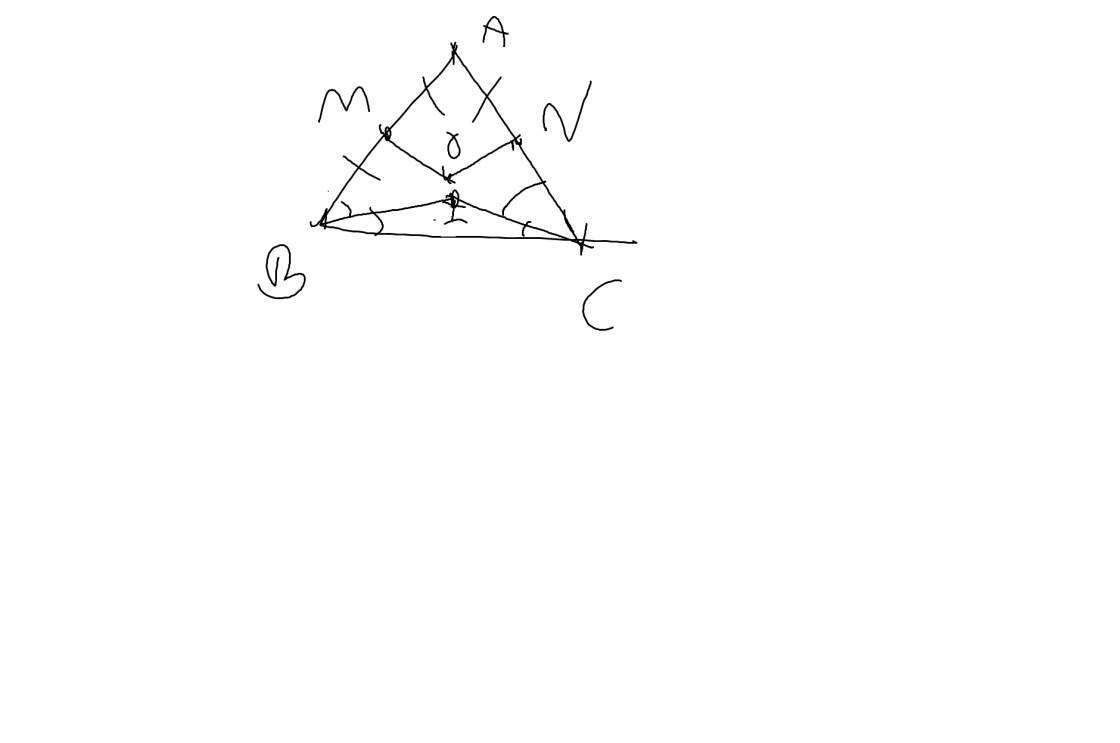
a: ta có: \(AM=MB=\dfrac{AB}{2}\)
\(AN=NC=\dfrac{AC}{2}\)
mà AB=AC
nên AM=MB=AN=NC
Xét ΔAMO vuông tại M và ΔANO vuông tại N có
AO chung
AM=AN
Do đó: ΔAMO=ΔANO
b: O nằm trên đường trung trực của AB
=>OA=OB
O nằm trên đường trung trực của AC
=>OA=OC
Do đó: OA=OB=OC
c: Xét ΔABO và ΔACO có
AB=AC
BO=CO
AO chung
Do đó: ΔABO=ΔACO
=>\(\widehat{BAO}=\widehat{CAO}\)
=>AO là phân giác của góc BAC
d: Ta có: \(\widehat{IBC}=\dfrac{\widehat{ABC}}{2}\)
\(\widehat{ICB}=\dfrac{\widehat{ACB}}{2}\)
mà \(\widehat{ABC}=\widehat{ACB}\)(ΔABC cân tại A)
nên \(\widehat{IBC}=\widehat{ICB}\)
=>ΔIBC cân tại I
=>I nằm trên đường trung trực của BC(1)
Ta có: AB=AC
=>A nằm trên đường trung trực của BC(2)
ta có: OB=OC
=>O nằm trên đường trung trực của BC(3)
Từ (1),(2),(3) suy ra A,O,I thẳng hàng
Bài 2:
a: \(x\left(2x+x^2\right)+B\left(x\right)=\left(x^2-6x\right)\left(x+1\right)\)
=>\(B\left(x\right)=x^3+x^2-6x^2-6x-2x^2-x^3\)
=>\(B\left(x\right)=-7x^2-6x\)
b: \(B\left(x\right)=-7x^2-6x\)
Bậc là 2
Hệ số cao nhất là -7
Hệ số tự do là 0
Bài 4:
a: \(VT=\left(a+1\right)\left(a^2-a+1\right)\)
\(=a^3-a^2+a+a^2-a+1\)
\(=a^3+1=VP\)
b: \(VT=\left(a+1\right)\left(a^3-a^2+a-1\right)\)
\(=a^4-a^3+a^2-a+a^3-a^2+a-1\)
\(=a^4-1=VP\)