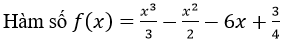
Trong toán học, parabol  là một đường conic được tạo bởi giao của một hình nón và một mặt phẳng song song với đường sinh của hình đó. Một parabol cũng có thế được định nghĩa như một tập hợp các điểm trên mặt phẳng cách đều một điểm cho trước (tiêu điểm) và một đường thẳng cho trước (đường chuẩn).

1. Định nghĩa Parabol

trong toán học, parabol là một đường conic được tạo bởi giao của một hình nón và một mặt phẳng song song với đường sinh của hình đó. Hoặc người ta có thể định nghĩa Parabol là quỹ tích các điểm cách đều một điểm và một đường thẳng cho trước. Cho một điểm F cố định và một đường thẳng Δ cố định không đi qua F. Thì đường Parabol là tập hợp tất cả các điểm M cách đều F và Δ. Trong đó: Điểm F được coi là tiêu điểm của Parabol Đường thẳng Δ được gọi là đường chuẩn của parabol. Khoảng cách từ F đến Δ được gọi là tham số tiêu của parabol. Một parabol chỉ có một trục đối xứng duy nhất, đi qua tiêu điểm và vuông góc với đường chuẩn của nó. Giao điểm của trục này và parabol được gọi là đỉnh. Một parabol quay xung quanh trục của nó trong không gian ba chiều sẽ tạo ra một hình paraboloid.

2. Phương trình Parabol 

2.1 Phương trình tổng quát của Parabol Dạng tổng quát của phương trình Parabol có dạng: (Ax + By)2 + Cx + Dy + E = 0 Phương trình này được rút ra từ phương trình tổng quát của các đường Conic và tính chất của đường parabol. Trong thực thế, ta có thể thấy đường parabol là đồ thị của hàm số bậc 2 có dạng: y = ax2+ bx + c.Trong đó: Hoành độ của tiêu điểm x = -b2a Thay x vào phương trình tổng quát ta tính được y = c -b2 -14a 2.2 Phương trình chính tắc của Parabol Phương trình chính tắc của Parabol được biểu diễn dưới dạng: y2 = 2px (với p >0)

3.1 Cách vẽ Parabol bằng thước và compa Bước 1: Khảo sát các điểm thuộc Parabol (Vì Parabol là đường đối xứng nhau nên chúng ta chỉ cần khảo sát 1 nửa parabol) Bước 2: Xác định trục đối xứng của Parabol (Kẻ đường thẳng đi qua điểm F cho trước và vuông góc với đường chuẩn), gọi giao điểm là O Bước 3: Lấy M là trung điểm của OF, chọn một điểm M1 bất kỳ thuộc đoạn MF. Kẻ đường thẳng đi qua M1 và song song với đường thẳng cho trước. Bước 4: Dùng Compa, quay 1 cung có bán kính OM1, cung và đường thẳng qua M1 cắt nhau ở đâu, ta được 1 điểm thuộc Parabol. Bước 5: Lấy thêm các điểm bất kỳ thuộc đoạn MF rồi làm tương tự các bước trên. Cuối cùng, ta nối các điểm thuộc parabol, là tạo thành đường parabol hoàn chỉnh.

3.2 Cách vẽ parabol thông qua đồ thị hàm số bậc 2 Trên thực tế, cách vẽ trên không được ứng dụng nhiều, thay vào đó, người ta thường biểu diễn parabol thông qua đồ thị hàm số bậc 2. Dưới đây mình sẽ giới thiệu cách vẽ hàm số bậc 2 nhé! Ví dụ hàm số bậc 2 có dạng: y = ax2 + bx + c (a # 0) Bước 1: Xác định tọa độ của đỉnh, hoành độ x = -b2a, tung độ y = -4a(một cách dễ dàng hơn, sau khi tính được hoành độ x, ta thay vào phương trình sẽ tim ra tung độ y. Bước 2: Vẽ trục đối xứng (đi qua đỉnh và song song với trục tung) Bước 3: Tìm một số điểm đặc biệt thuộc đồ thị hàm số. Đơn giản các bạn chỉ cần chọn các giá trị khác nhau của x, thay vào phương trình sẽ tìm ra y. Các bạn nên tìm khoảng 5 đến 7 điểm khác nhau thuộc đồ thị hàm số, càng nhiều điểm thì độ chính xác càng cao. Sau đó nối các điểm vào với nhau là được đồ thị hàm số bậc 2 là một đường parabol.

để viết được phương trình Parabol, trước hết ta cần giả sử dạng của Parabol theo phương trình tổng quát: y = ax2 + bx + c (a # 0). Sau đó, dựa theo các điều kiện của đề bài ra để tìm ra các hệ số a,b,c. Một số điều kiện thường gặp có thể kể đến như: Cho Parabol đi qua một điểm cố định A(x0,y0), ta có y = ax02 + bx0 + c Cho biết tọa độ đỉnh I(x0,y0), thay tọa độ vào công thức đỉnh ứng với các hệ số Cho biết trục đối xứng là x = x0, ta có x0 = -b2a

Giả sử đa diện (H)(H) có các đỉnh là A1,…AdA1,…Ad, gọi m1,…mdm1,…md lần lượt là số các mặt của (H)(H) nhận chúng là đỉnh chung, ở đó m1,…mdm1,…md là những số lẻ.

Như vậy mỗi đỉnh AkAk có mkmk cạnh đi qua.

Ta có: đỉnh A1A1 có m1m1 cạnh đi qua.

đỉnh A2A2 có m2m2 cạnh đi qua.

...

đỉnh AdAd có mdmd cạnh đi qua.

Do đó số các cạnh (có thể trùng nhau) của đa diện là m1+m2+...+mdm1+m2+...+md.

Tuy nhiên, do mỗi cạnh là cạnh chung của đúng hai mặt nên số cạnh ở trên được đếm hai lần.

Vậy số cạnh thực tế của (H)(H) bằng

c=12(m1+m2+...+md)c=12(m1+m2+...+md)      

Vì cc là số nguyên, m1,…mdm1,…md là những số lẻ nên dd phải là số chẵn.

Ví dụ : Hình chóp ngũ giác.

Đỉnh S là đỉnh chung của 5 mặt, tất cả các đỉnh còn lại là đỉnh chung của 3 mặt, hình chóp ngũ giác có 6 đỉnh

giup mình cày Sp vơi

T
L câu hỏi là gì zậy bn :)

HT

7b/5 ) trong dod#$^&*())*&YYÚGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGG
thực ra tui ko biết đâu

TL:

D)Đồng biến trên khoảng (-; +∞)

_HT_

Hàm số: \(f\left(x\right)=\frac{x^3}{3}-\frac{x^2}{2}-6x+\frac{3}{4}\)

A) Đồng biến trên khoảng (-2; 3)

B) Nghịch biến trên khoảng (-2; 3)

C) Nghịch biến trên khoảng (-∞; -2)

D) Đồng biến trên khoảng (-; +∞)

bằng 499086803 

240

Hokk tốt

Trả lời 

240

Hok tốt 

sao lại tự nhiên có "Unexpected text node:"

Khó ghê

. Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a va cạnh bên bằng  a√2

`âu 1. Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a va cạnh bên bằng a2–√. a) Tính thể tích của hình chóp đã cho. b) Tính bán kính mặt cầu ngoại tiếp hình chóp S.ABCD. c) Gọi A’ và C’ lần lượt là trung điểm của hai cạnh SA và SC. Chứng minh rằng hai hình chóp A’.ABCD và C’.CBAD bằng nhau. Câu 2. Trong không gian tọa độ Oxyz, cho các điểm A(4; -1; 2), B(1; 2; 2) và C(1; -1; 5). a) Chứng minh rằng ABC là tam giác đều. b) Viết phương trình mp(ABC). Tính thể tích khối tứ diện giới hạn bởi mp(ABC) và các mặt phẳng tọa độ. c) Viết phương trình trục của đường tròn ngoại tiếp tam giác ABC. d) Tìm tọa độ điểm D sao cho ABCD là tứ diện đều.`

`âu 1. Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a va cạnh bên bằng a2–√. a) Tính thể tích của hình chóp đã cho. b) Tính bán kính mặt cầu ngoại tiếp hình chóp S.ABCD. c) Gọi A’ và C’ lần lượt là trung điểm của hai cạnh SA và SC. Chứng minh rằng hai hình chóp A’.ABCD và C’.CBAD bằng nhau. Câu 2. Trong không gian tọa độ Oxyz, cho các điểm A(4; -1; 2), B(1; 2; 2) và C(1; -1; 5). a) Chứng minh rằng ABC là tam giác đều. b) Viết phương trình mp(ABC). Tính thể tích khối tứ diện giới hạn bởi mp(ABC) và các mặt phẳng tọa độ. c) Viết phương trình trục của đường tròn ngoại tiếp tam giác ABC. d) Tìm tọa độ điểm D sao cho ABCD là tứ diện đều.`

TL :

\(9.655.226.222.987\)

\(=5895.50172.987\)

\(=295763940.987\)

\(=291919008780\)

TL

tham khảo nha bn chứ tui ko bít làm :}} 

 (y’ = 4x – 3;y’ = 0 Leftrightarrow x = {3 over 4};yleft( {{3 over 4}} ight) =  – {1 over 8})

Đỉnh (Ileft( {{3 over 4}; – {1 over 8}} ight))

Công thức chuyển trục tọa độ tịnh tiến theo

(overrightarrow {OI} :left{ matrix{
x = X + {3 over 4} hfill cr
y = Y – {1 over 8} hfill cr} ight.)

Phương trình của ((P)) đối với hệ tọa độ (IXY) là

(Y – {1 over 8} = 2{left( {X + {3 over 4}} ight)^2} – 3left( {X + {3 over 4}} ight) + 1 Leftrightarrow Y = 2{X^2})

k cho tui nick naruto nha thank