Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) -3 < x < 3
=> \(x=-2;-1;0;1;2\)
Tổng x là \(-2+\left(-1\right)+0+1+2=0\)
b) \(-5\le x< 4\)
=> \(x=-5;-4;-3;-2;-1;0;1;2;3\)
Tổng x là \(-5+\left(-4\right)+\left(-3\right)+\left(-2\right)+\left(-1\right)+0+1+2+3=-9\)
c) -7 < x < 11
=> \(x=-6;-5;-4;-3;-2;-1;0;1;2;3;4;5;6;7;8;9;10\)
Tổng x là
\(-6+\left(-5\right)+\left(-4\right)+\left(-3\right)+\left(-2\right)+\left(-1\right)+0+1+2+3+4+5+6+7+8+9+10=34\)
d) \(15\le x\le13\)
Không có x nào thoả mãn đề bài
a) -2;-1;0;1;2
b)-5;-4;-3;-2;-1;0;1;2;3
c)-6;-5;-4;-3;-2;-1;0;1;2;3;4;5;6;7;8;9;10
d) mình chịu nhé

a) \(\left(-214\right)+\left(-120\right)+\left(-16\right)\)
\(=\left[\left(-214\right)+\left(-16\right)\right]+\left(-120\right)\)
\(=\left(-230\right)+\left(-120\right)\)
\(=-350\)
b) \(34+\left(-100\right)+\left(-34\right)+100\)
\(=\left[34+\left(-34\right)\right]+\left[\left(-100\right)+100\right]\)
\(=0+0\)
\(=0\)
c) \(\left(-2021\right)+\left(-999\right)+21+\left(-2001\right)\)
\(=\left[\left(-2021\right)+21\right]+\left[\left(-999\right)+\left(-2001\right)\right]\)
\(=\left(-2000\right)+\left(-3000\right)\)
\(=-5000\)
d) \(-41\left(59+2\right)+59\left(41-2\right)\)
\(=-41.61+59.39\)
\(=-2501+2301\)
\(=-200\)
e) \(\left(-157\right).\left(127-316\right)-127.\left(316-157\right)\)
\(=\left(-157\right).127+\left(-157\right)\left(-316\right)+\left(-127\right).316+\left(-127\right).\left(-157\right)\)
\(=-157.127+157.316-127.316+127.157\)
\(=\left[-\left(127.157\right)+127.157\right]+\left(157.316-127.316\right)\)
\(=0+316.\left(157-127\right)\)
\(=316.30\)
\(=9480\)
f) \(-1500-\left\{5^3.2^3-11.\left[7^2-5.2^3+8.\left(11^2-121\right)\right]\right\}.\left(-2\right)\)
\(=-1500-125.8-11.\left[49.-5.2^3.\left(121-121\right)\right]\)
\(=-1500-\left[1000-11.\left(49-0\right)\right]\)
\(=-1500-\left(1000-539\right)\)
\(=-2500+539\)
\(=-1961\)

Gọi số nguyên thứ nhất thỏa mãn đề bài là: \(x\) (\(x\in\) Z)
Thì ba số nguyên tiếp thỏa mãn đề bài lần lượt là: \(x\); \(x\) + 1; \(x\) + 2
Tổng của ba số nguyên liên tiếp là: \(x\) + \(x\) + 1 + \(x\) + 2 = 3\(x\) + 3
Theo bài ra ta có: 3\(x\) + 3 = -9
3\(x\) = - 9 - 3
3\(x\) = -12
\(x\) = -12:3
\(x\) = -4
Vậy ba số nguyên liên tiếp thỏa mãn đề bài lần lượt là: -4; -3; -2
Tích của ba số nguyên liên tiếp là: -4.(-3).(-2) = -24
Kết luận: đáp án đúng mà người B cần đưa ra là: -24

À mình nhầm 1 chút. Tích \(P=\left(1+1\right)\left(2+1\right)\left(3+1\right)...\left(2023+1\right)\) và do đó nếu \(a_0\) là số cuối cùng trên bảng thì\(\dfrac{1}{a_0}+1=\left(1+1\right)\left(2+1\right)\left(3+1\right)...\left(2023+1\right)\) hay \(a_0=\dfrac{1}{2.3.4...2024-1}\). Vậy số cuối cùng là \(\dfrac{1}{2.3.4...2024-1}\)
Nếu trên bảng có các số \(a_1,a_2,...,a_n\) thì ta xét tích \(P=\left(\dfrac{1}{a_1}+1\right)\left(\dfrac{1}{a_2}+1\right)...\left(\dfrac{1}{a_n}+1\right)\). Sau mỗi bước, ta thay 2 số \(a_i,a_j\) bằng số \(a_k=\dfrac{a_ia_j}{a_i+a_j+1}\). Khi đó \(\dfrac{1}{a_k}+1=\dfrac{a_i+a_j+1}{a_ia_j}+1=\dfrac{1}{a_i}+\dfrac{1}{a_j}+\dfrac{1}{a_ia_j}+1\) \(=\dfrac{1}{a_j}\left(\dfrac{1}{a_i}+1\right)+\left(\dfrac{1}{a_i}+1\right)\) \(=\left(\dfrac{1}{a_i}+1\right)\left(\dfrac{1}{a_j}+1\right)\)
Như vậy, sau phép biến đổi ban đầu, tích\(P=\left(\dfrac{1}{a_1}+1\right)\left(\dfrac{1}{a_2}+1\right)...\left(\dfrac{1}{a_k}+1\right)...\left(\dfrac{1}{a_n}+1\right)\)
\(P=\left(\dfrac{1}{a_1}+1\right)\left(\dfrac{1}{a_2}+1\right)...\left(\dfrac{1}{a_i}+1\right)\left(\dfrac{1}{a_j}+1\right)...\left(\dfrac{1}{a_n}+1\right)\)
Là không thay đổi. Vì vậy, số cuối cùng còn lại trên bảng chính là giá trị của tích P. Lại có
\(P=\left(1+1\right)\left(\dfrac{1}{2}+1\right)\left(\dfrac{1}{3}+1\right)...\left(\dfrac{1}{2023}+1\right)\)
\(P=2.\dfrac{3}{2}.\dfrac{4}{3}...\dfrac{2024}{2023}=2024\)
Như vậy, số cuối cùng trên bảng sẽ bằng 2024.

Đổi 2 m = 200 cm
Nửa chu vi là: 200 : 2 = 100 (cm)
Vì bớt chiều dài đi 20 cm thì được hình thoi nên chiều dài hơn chiều rộng là 20 cm
Gọi chiều rộng là \(x\) (cm) \(x\) > 0. Khi đó chiều dài là: \(x\) + 20 (cm)
Theo bài ra ta có phương trình: \(x\) + 20 + \(x\) = 100
⇒2\(x\) = 100 - 20 ⇒ 2\(x\) = 80 ⇒ \(x\) = 80: 2⇒ \(x\) = 40
Vậy chiều rộng của hình bình hành là: 40 cm
Chiều dài của hình bình hành là: 40 + 20 = 60 (cm)
Vì hình thoi cũng là hình bình hành nên công thức tính diện tích của hình bình hành cũng là công thức tính diện tích của hình thoi.
Đổi 6 dm2 = 600 cm2
Chiều cao của hình thoi là: 600: 40 = 15 (cm)
Chiều cao của hình thoi chính là chiều cao của hình bình hành.
Diện tích hình bình hành là: 60 \(\times\) 15 = 900 (cm2)
Đáp số: 900 cm2
Chọn 900 cm2

Độ dài cạnh CD hay AB là: \(480:30=16\left(cm\right)\)
Độ dài CE là: \(30.2=60\left(cm\right)\)
Độ dài cạnh AD hay BC là: \(480:60=8\left(cm\right)\)
Chu vi hình bình hành ABCD là: \(\left(16+8\right).2=48\left(cm\right)\)

\(-\dfrac{4}{3}\cdot x=\dfrac{2}{3}:\dfrac{7}{12}:\dfrac{4}{18}\)
\(\Rightarrow-\dfrac{4}{3}\cdot x=\dfrac{36}{7}\)
\(\Rightarrow x=\dfrac{\dfrac{36}{7}}{-\dfrac{4}{3}}=-\dfrac{27}{7}\)
-\(\dfrac{4}{3}\).\(x\) = \(\dfrac{2}{3}\): \(\dfrac{7}{12}\):\(\dfrac{4}{18}\)
-\(\dfrac{4}{3}.x\) = \(\dfrac{2}{3}\times\)\(\dfrac{12}{7}\)\(\times\)\(\dfrac{18}{4}\)
-\(\dfrac{4}{3}.\)\(x\)= \(\dfrac{36}{7}\)
\(x\) = \(\dfrac{36}{7}\):(-\(\dfrac{4}{3}\))
\(x\) = - \(\dfrac{27}{7}\)

A = \(\dfrac{1}{\left|x+1\right|+\left|x-2022\right|}\)
Đặt B = \(\left|x+1\right|+\left|x-2022\right|\)
\(\left|x-2022\right|\) = \(\left|2022-x\right|\) ⇒ B = \(\left|x+1\right|+\left|2022-x\right|\)
B =\(\left|x+1\right|+\left|2022-x\right|\) ≥ \(\left|x+1+2022-x\right|\) = 2023
B(min) = 2023 ⇔ (\(x+1\))(2022-\(x\)) \(\ge\) 0
Lập bảng ta có:
| \(x\) | -1 2022 |
| \(x+1\) | - 0 + | + |
| \(2022-x\) | + | + 0 - |
| (\(x+1\))(\(2022-x\)) | - 0 + 0 - |
Theo bảng trên ta có: B(min) = 2023 ⇔ -1 ≤ \(x\) ≤ 2022
A = \(\dfrac{1}{\left|x+1\right|+\left|x-2022\right|}\)
Vì A dương nên A(max) ⇔ B(min) ⇔ B = 2023
A(max) = \(\dfrac{1}{2023}\) ⇔ -1 ≤ \(x\) ≤ 2022




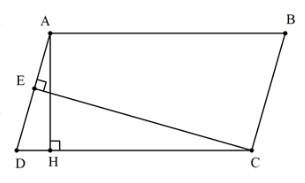
\(a,\left(-8.2+17\right).\left[x+\left(-2\right).3\right]=20\)
\(\Rightarrow\left(-16+17\right).\left(x-6\right)=20\)
\(\Rightarrow1.\left(x-6\right)=20\)
\(\Rightarrow x=20+6\)
\(\Rightarrow x=26\)
\(b,\left(-5\right).x+5=\left(-3\right).\left(-8\right)+6\)
\(\Rightarrow-5x+5=24+6\)
\(\Rightarrow-5x+5=30\)
\(\Rightarrow-5x=25\)
\(\Rightarrow x=25:\left(-5\right)\)
\(\Rightarrow x=-5\)
\(c,-152-\left(3x+1\right)=\left(-2\right).\left(-27\right)\)
\(\Rightarrow-152-3x-1=54\)
\(\Rightarrow-3x=54+152+1\)
\(\Rightarrow-3x=207\)
\(\Rightarrow x=-69\)
\(d,\left(x+6\right)\left(x-4\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x+6=0\\x-4=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=-6\\x=4\end{matrix}\right.\)
a) \(\left(-8,2+17\right).\left(x+\left(-2\right).3\right)=20\)
\(\Rightarrow8,8\cdot\left(x-6\right)=20\)
\(\Rightarrow x-6=\dfrac{25}{11}\)
\(\Rightarrow x=\dfrac{91}{11}\)
b) \(\left(-5\right)x+5=\left(-3\right).\left(-8\right)+6\)
\(\Rightarrow\left(-5\right)x+5=30\)
\(\Rightarrow\left(-5\right)x=25\)
\(\Rightarrow x=-5\)
c) \(-152-\left(3x+1\right)=\left(-2\right).\left(-27\right)\)
\(\Rightarrow-152-\left(3x+1\right)=54\)
\(\Rightarrow-\left(3x+1\right)=206\)
\(\Rightarrow-3x-1=206\)
\(\Rightarrow-3x=207\)
\(\Rightarrow x=-69\)
d) \(\left(x+6\right)\left(x-4\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x+6=0\\x-4=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=-6\\x=4\end{matrix}\right.\)