Lời giải:

Gọi hai số lần lượt là $a,b$. Theo bài ra ta có:

$a+b=25$

$2a-3b=5$

$\Rightarrow 3(a+b)+(2a-3b)=25.3+5$

$\Rightarrow 5a=80$

$\Rightarrow a=80:5=16$

$b=25-16=9$

Vậy hai số cần tìm là $16$ và $9$

a: Ta có: QN\(\perp\)MP(MNPQ là hình vuông)

QN\(\perp\)MS(SM\(\perp\)(MNPQ))

MP,MS cùng thuộc mp(SMP)

Do đó: QN\(\perp\)(SMP)

a.

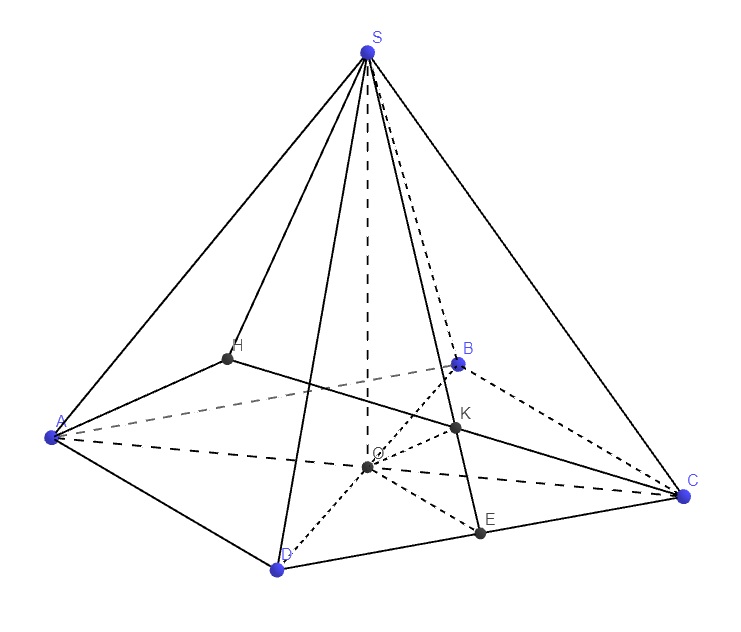
Do chóp S.ABCD đều \(\Rightarrow SO\perp\left(ABCD\right)\)

\(\Rightarrow\) O là hình chiếu vuông góc của S lên (ABCD)

\(\Rightarrow\Delta OAB\) là hình chiếu vuông góc của \(\Delta SAB\) lên (ABCD)

b.

Gọi E là trung điểm CD \(\Rightarrow OE\) là đường trung bình tam giác BCD

\(\Rightarrow OE||BC\Rightarrow OE\perp CD\)

\(\Rightarrow CD\perp\left(SOE\right)\)

Trong mp (SOE), từ O kẻ \(OK\perp SE\)

\(OK\in\left(SOE\right)\Rightarrow CD\perp OK\)

\(\Rightarrow OK\perp\left(SCD\right)\)

Trong mp (ACK), qua A kẻ đường thẳng song song OK cắt CK kéo dài tại H

\(\Rightarrow AH\perp\left(SCD\right)\Rightarrow SH\) là hình chiếu vuông góc của SA lên (SCD)

\(\Rightarrow\widehat{ASH}\) là góc giữa SA và (SCD) hay \(\widehat{ASH}=\varphi\)

\(OE=\dfrac{1}{2}BC=\dfrac{a}{2}\) 

Áp dụng hệ thức lượng trong tam giác vuông SOE:

\(OK=\dfrac{SO.OE}{\sqrt{SO^2+OE^2}}=\dfrac{a\sqrt{5}}{5}\)

O là trung điểm AC và \(OK||SH\Rightarrow OK\) là đường trung bình tam giác CAH

\(\Rightarrow AH=2OK=\dfrac{2a\sqrt{5}}{5}\)

\(OA=\dfrac{1}{2}AC=\dfrac{a\sqrt{2}}{2}\Rightarrow SA=\sqrt{SO^2+OA^2}=\dfrac{a\sqrt{6}}{2}\)

\(\Rightarrow sin\varphi=\dfrac{AH}{SA}=\dfrac{2\sqrt{30}}{15}\)

a) \(n\left(\Omega\right)=48\)

Gọi A là biến cố: "Bạn được chọn thích bóng chuyền hoặc bóng bàn."

Áp dụng công thức bù trừ, ta có:

\(n\left(A\right)=19+13-8=24\)

\(\Rightarrow P\left(A\right)=\dfrac{n\left(A\right)}{n\left(\Omega\right)}=\dfrac{24}{48}=\dfrac{1}{2}\)

b) Xác suất là \(1-\dfrac{1}{2}=\dfrac{1}{2}\)

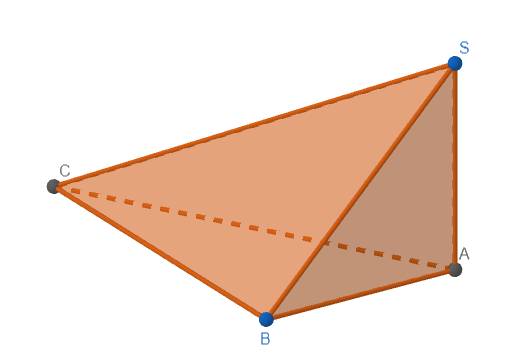
Ta có \(SA\perp\left(ABC\right)\) nên \(SA\perp BC\)

Lại có \(BC\perp AB\) nên \(CB\perp\left(SAB\right)\)

Do đó \(\widehat{SC,\left(SAB\right)}=\widehat{CSB}\)

Mặt khác, \(CB\perp\left(SAB\right)\Rightarrow CB\perp SB\) \(\Rightarrow\Delta SBC\) vuông tại B

Có \(SC=\sqrt{SA^2+AC^2}=\sqrt{a^2+\left(2a\right)^2}=a\sqrt{5}\)

\(CB=AC.\cos30^o=2a.\dfrac{\sqrt{3}}{2}=a\sqrt{3}\)

\(\Rightarrow\sin\widehat{CSB}=\dfrac{CB}{CS}=\dfrac{a\sqrt{3}}{a\sqrt{5}}=\sqrt{\dfrac{3}{5}}\)

\(\Rightarrow\widehat{CSB}=arc\sin\left(\sqrt{\dfrac{3}{5}}\right)\approx50,768^o\)

Vậy \(\widehat{SC,\left(SAB\right)}\approx50,768^o\)

 Mình gửi đáp án rồi đó nhưng vì có hình nên nó chưa duyệt lên được. Bạn vào trang cá nhân của mình xem nhé.

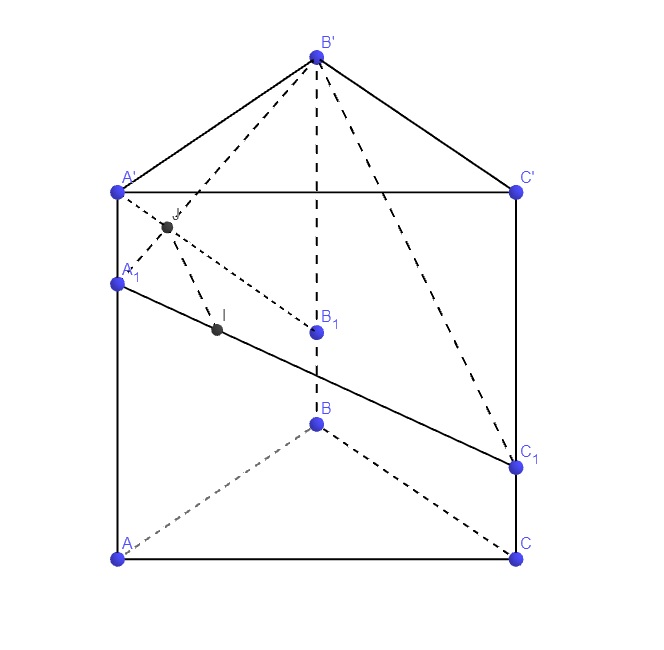
Trong mp (ABB'A'), gọi J là giao điểm \(A'B_1\) và \(A_1B'\)

Trong mp \(\left(A_1B'C_1\right)\) qua J kẻ đường thẳng song song \(B'C_1\) cắt \(A_1C_1\) tại I

Áp dụng định lý Thales: \(\dfrac{A_1J}{JB'}=\dfrac{A'A_1}{B'B_1}=\dfrac{1}{3}\)

\(\Rightarrow\dfrac{A_1J}{A_1B'}=\dfrac{1}{4}\)

\(C'C_1=\dfrac{3}{4}C'C=\dfrac{3a}{2}\Rightarrow B'C_1=\sqrt{B'C'^2+C'C_1^2}=\dfrac{a\sqrt{13}}{2}\)

Áp dụng định lý Thales: \(\dfrac{IJ}{B'C_1}=\dfrac{A_1J}{A_1B'}=\dfrac{1}{4}\Rightarrow IJ=\dfrac{1}{4}B'C_1=\dfrac{a\sqrt{13}}{8}\)