a: Ta có: mn//xy

=>\(\widehat{mAB}=\widehat{ABy}\)(hai góc so le trong)

=>\(\widehat{mAB}=60^0\)

b:

Ta có: \(\widehat{yBc}+\widehat{yBA}=180^0\)(hai góc kề bù)

=>\(\widehat{yBc}=180^0-60^0=120^0\)

Bz là phân giác của góc yBc

=>\(\widehat{yBz}=\widehat{cBz}=\dfrac{\widehat{yBc}}{2}=\dfrac{120^0}{2}=60^0\)

Ta có: \(\widehat{nAB}+\widehat{mAB}=180^0\)(hai góc kề bù)

=>\(\widehat{nAB}=180^0-60^0=120^0\)

At là phân giác của góc nAB

=>\(\widehat{nAt}=\widehat{tAB}=\dfrac{\widehat{nAB}}{2}=\dfrac{120^0}{2}=60^0\)

Ta có: \(\widehat{ABz}=\widehat{ABy}+\widehat{yBz}=60^0+60^0=120^0\)

Ta có: \(\widehat{ABz}+\widehat{BAt}=120^0+60^0=180^0\)

mà hai góc này là hai góc ở vị trí trong cùng phía

nên At//Bz

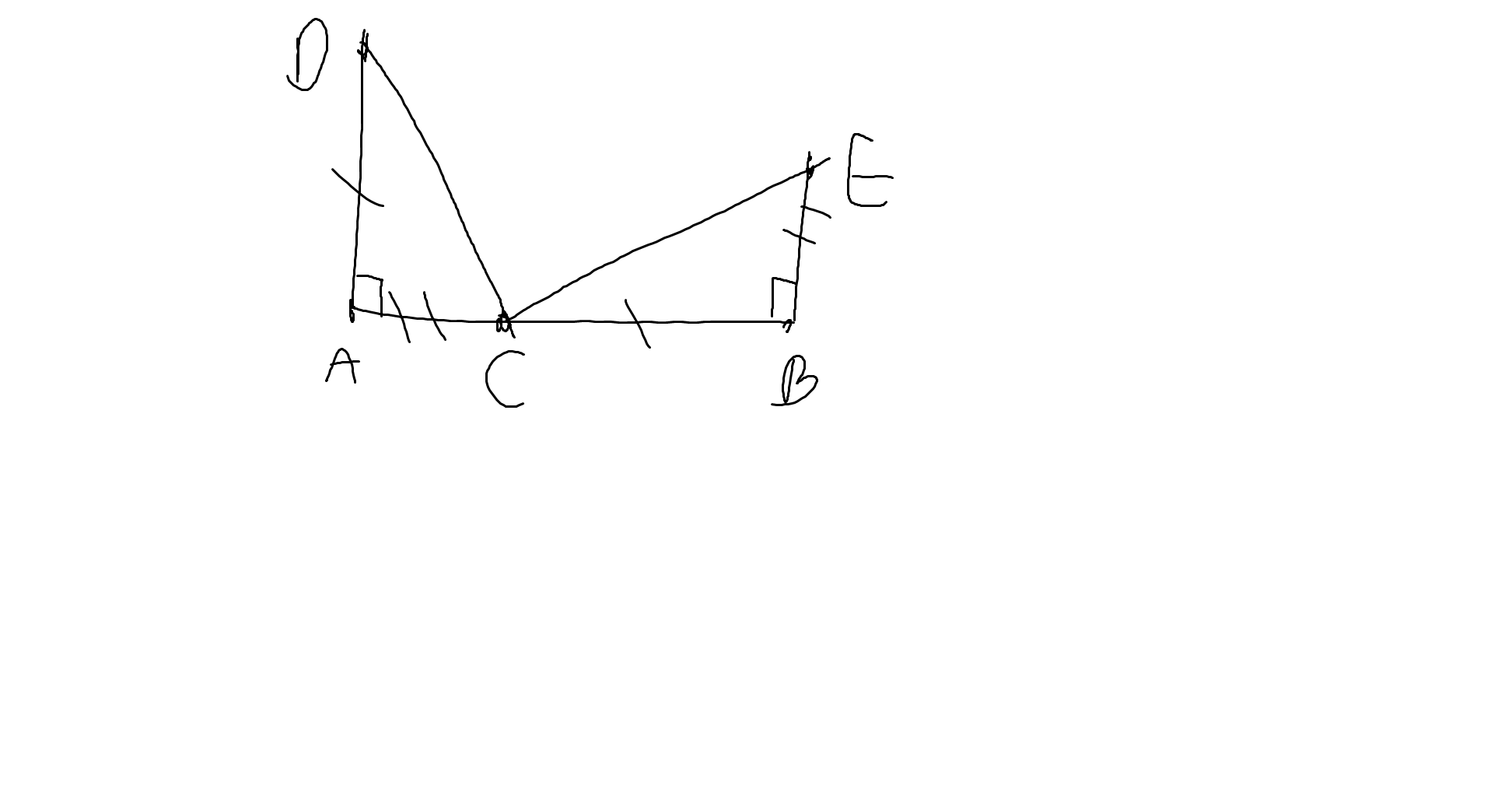
a: Xét ΔDAC vuông tại A và ΔCBE vuông tại B có

DA=CB

AC=BE

Do đó: ΔDAC=ΔCBE

b: ΔDAC=ΔCBE

=>\(\widehat{DCA}=\widehat{CEB}\)

=>\(\widehat{DCA}+\widehat{ECB}=90^0\)

Ta có: \(\widehat{DCA}+\widehat{ECB}+\widehat{DCE}=180^0\)

=>\(\widehat{DCE}+90^0=180^0\)

=>\(\widehat{DCE}=90^0\)

=>CD\(\perp\)CE

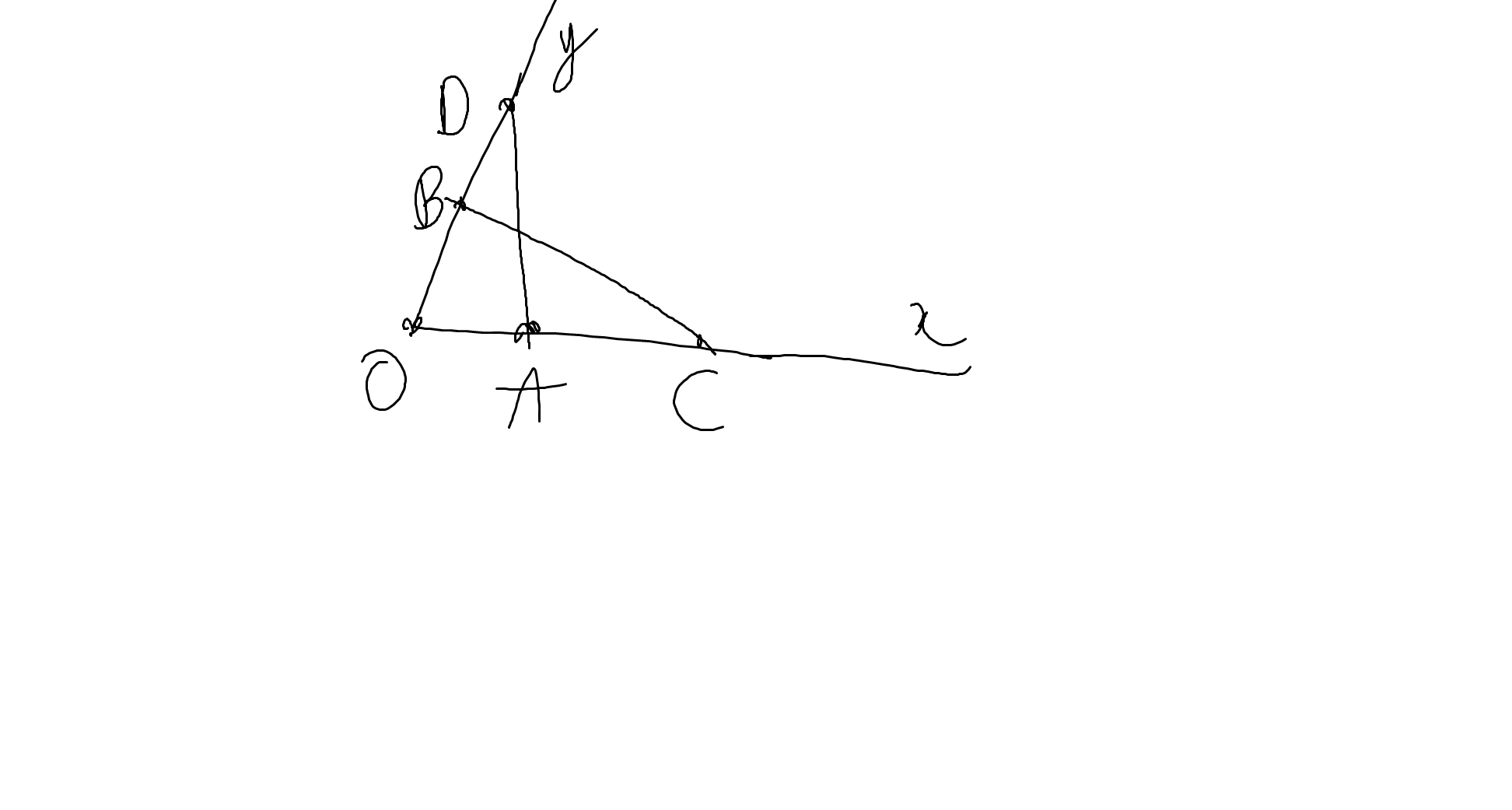
Xét ΔOAD và ΔOBC có

OA=OB

\(\widehat{AOD}\) chung

OD=OC

Do đó: ΔOAD=ΔOBC

=>AD=BC

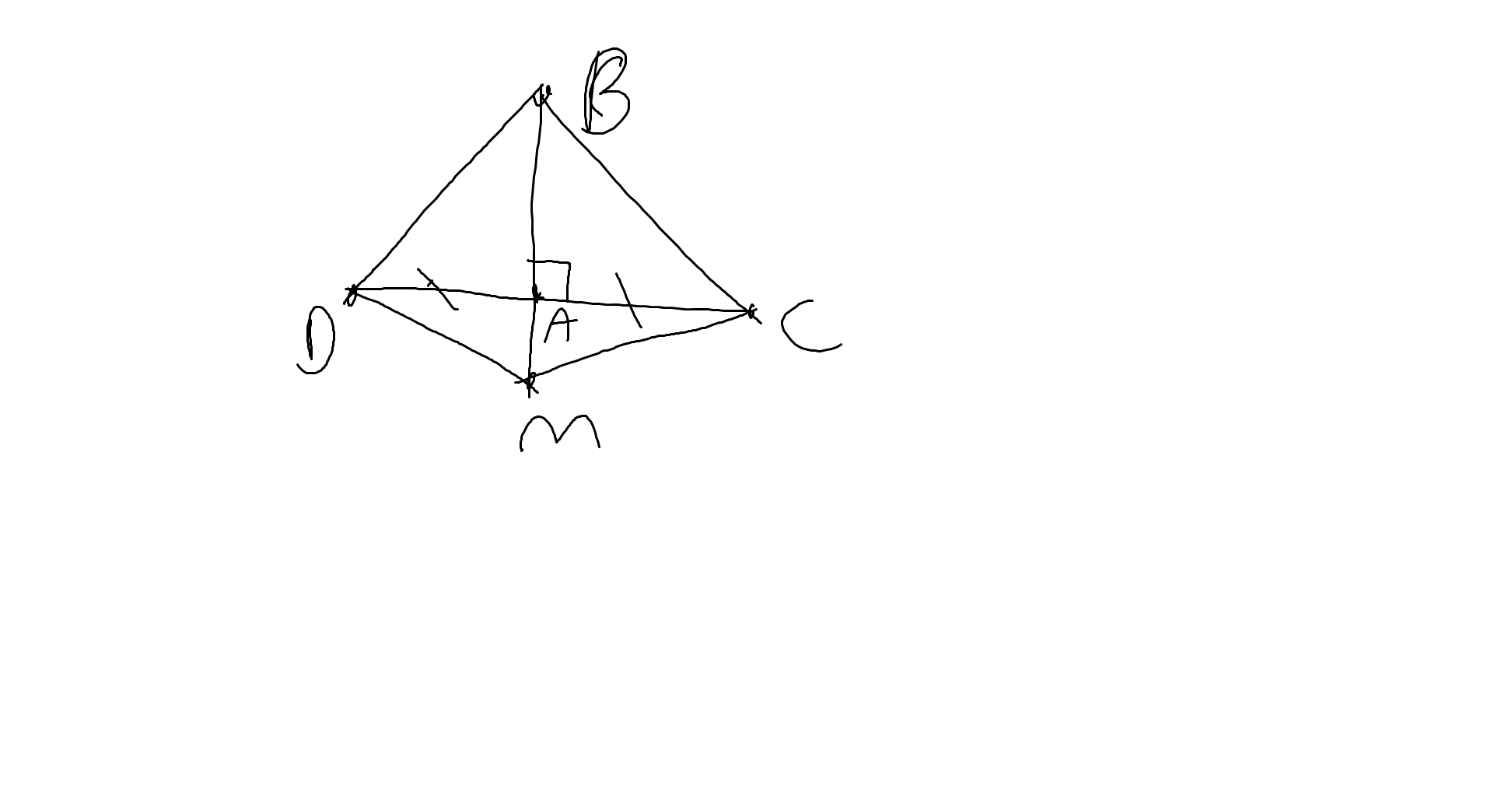
a: Xét ΔABD vuông tại A và ΔABC vuông tại A có

AB chung

AD=AC

Do đó: ΔABD=ΔABC

b: ΔABD=ΔABC

=>BD=BC

ΔABD=ΔABC

=>\(\widehat{ABD}=\widehat{ABC}\)

=>\(\widehat{MBC}=\widehat{MBD}\)

Xét ΔMBC và ΔMBD có

MB chung

\(\widehat{MBC}=\widehat{MBD}\)

BC=BD

Do đó: ΔMBC=ΔMBD

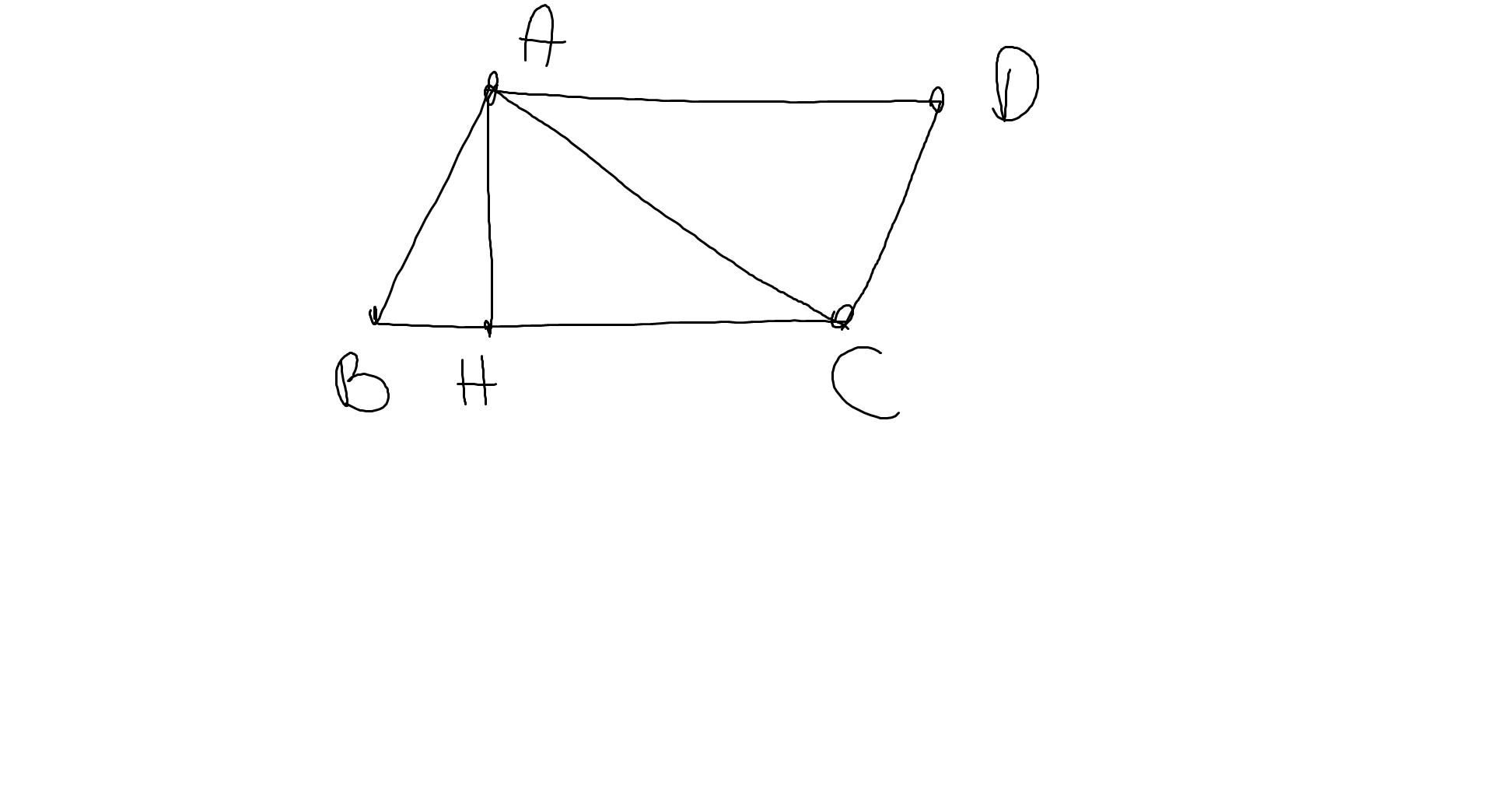
a: Xét ΔABC và ΔCDA có

AB=CD

AC chung

BC=DA

Do đó: ΔABC=ΔCDA

=>\(\widehat{BAC}=\widehat{DCA}\)

mà hai góc này là hai góc ở vị trí so le trong

nên AB//CD

b: ΔABC=ΔCDA

=>\(\widehat{ACB}=\widehat{DAC}\)

mà hai góc này là hai góc ở vị trí so le trong

nên AD//BC

mà AH\(\perp\)BC

nên AH\(\perp\)AD

a: Xét ΔMAC và ΔMEB có

MA=ME

\(\widehat{AMC}=\widehat{EMB}\)(hai góc đối đỉnh)

MC=MB

Do đó: ΔMAC=ΔMEB

=>\(\widehat{MAC}=\widehat{MEB}\)

mà hai góc này là hai góc ở vị trí so le trong

nên AC//EB

b: Xét ΔMAI và ΔMEK có

MA=ME

\(\widehat{MAI}=\widehat{MEK}\)(cmt)

AI=EK

Do đó: ΔMAI=ΔMEK

=>\(\widehat{AMI}=\widehat{EMK}\)

=>\(\widehat{EMK}+\widehat{EMI}=180^0\)

=>I,M,K thẳng hàng

Em cần làm gì với biể thức này? 

C = 25.{2 + 3.[5. (625.25]}

C = 25.{2 + 3.[5.15625]}

C = 25.{2 + 3.78125}

C = 25.{2 + 234375}

C = 25.234377

C = 5859425 

- \(\dfrac{5}{6}\).\(\dfrac{7}{11}\) + \(\dfrac{-5}{11}\).\(\dfrac{4}{6}\) + \(\dfrac{5}{6}\)

= - \(\dfrac{5}{6}\).\(\dfrac{7}{11}\)  \(-\dfrac{5}{6}\).\(\dfrac{4}{11}\) + \(\dfrac{5}{6}\) x 1

= - \(\dfrac{5}{6}\).(\(\dfrac{7}{11}\) + \(\dfrac{4}{11}\) - 1)

= - \(\dfrac{5}{6}\).(1 - 1)

= - \(\dfrac{5}{6}\).0

= 0

A =  1.2 + 2.3 + 3.4 + ... + n.(n + 1)

A = \(\dfrac{1}{3}\).(1.2.3 + 2.3.3 + 3.4.3 + ..+n(n+1).3)

A = \(\dfrac{1}{3}\).[1.2.3 + 2.3(4-1) + 3.4.(5-2)+..+n(n+1)(n+2- (n-1))]

A = \(\dfrac{1}{3}\).[1.2.3+2.3.4-1.2.3+3.4.5-2.3.4 +..+n(n+1)(n+2)-(n-1).n.(n+1)]

A = \(\dfrac{1}{3}\)[n.(n+1).(n+2)]