cho tập hợp A=[2m-1; 2m+9] và F= (0; 5). Biết rằng với a<m<b thì tập hợp A giao F khác tập rỗng. Tính P=2a+5b
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Hiệu số phần bằng nhau là 5-1=4(phần)
Tuổi của cha sau đây 3 năm nữa là:
24:4x5=30(tuổi)
Tuổi của cha hiện tại là 30-3=27(tuổi)
Tuổi của con hiện tại là 27-24=3(tuổi)

Đây là toán trồng cây dạng toán tư duy singapore, cấu trúc thi chuyên, thi học sinh giỏi các cấp. Hôm nay, Olm sẽ hướng dẫn các em giải chi tiết dạng này như sau:
Giải:
2m 8dm = 28dm
Số khúc gỗ cần cưa là: 28 : 4 = 7 (khúc)
Số lần cưa là: 7 - 1 = 6 (lần)
Thời gian cần để cưa là: 5 x 6 = 30 (phút)
Đáp số: 30 phút

\(E=1+2+2^2+...+2^{2022}\)
=>\(2E=2+2^2+2^3+...+2^{2023}\)
=>\(2E-E=2+2^2+...+2^{2023}-1-2-...-2^{2022}\)
=>\(E=2^{2023}-1\)

Số cây bút tổng cộng là \(7\cdot12=84\left(cây\right)\)
Vì 84:6=14 dư 0
nên cô giáo có thể chia đều số bút trên cho 6 tổ

Gọi số học sinh khối 6 là x(bạn)
(Điều kiện: \(x\in Z^+\))
Vì số học sinh nằm trong khoảng từ 350 đến 400 nên \(x\in\left\{350;351;...;400\right\}\)
Số học sinh này khi xếp thành hàng 10 thì dư 5 bạn nên x có chữ số tận cùng là 5
mà 350<=x<=400
nên \(x\in\left\{355;365;375;385;395\right\}\)
Số học sinh khi xếp thành hàng 8 thì dư 3 bạn
mà \(x\in\left\{355;365;375;385;395\right\}\)
nên \(x\in\left\{355;395\right\}\)
Số học sinh khi chia thành mỗi hàng 12 bạn thì dư 9 bạn nên x=395(nhận)
vậy: Số học sinh khối 6 là 395 bạn

1:
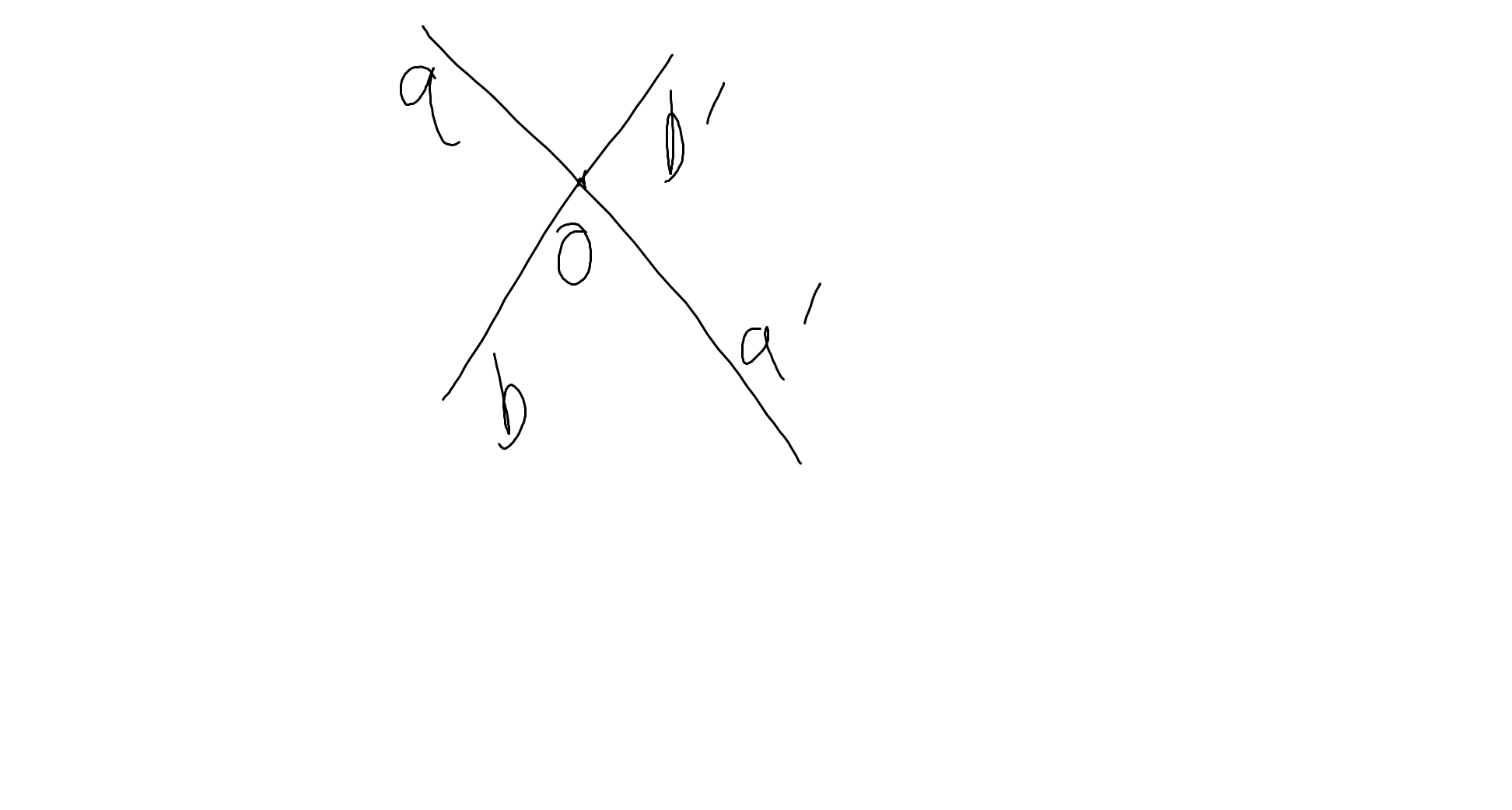
a: Các cặp góc đối đỉnh là: \(\widehat{aOb}';\widehat{a'Ob}\); \(\widehat{aOb};\widehat{a'Ob'}\)
b: Các cặp góc kề bù là: \(\widehat{aOb};\widehat{aOb'}\); \(\widehat{aOb'};\widehat{b'Oa'}\); \(\widehat{b'Oa'};\widehat{bOa'}\); \(\widehat{aOb};\widehat{a'Ob}\)
2:
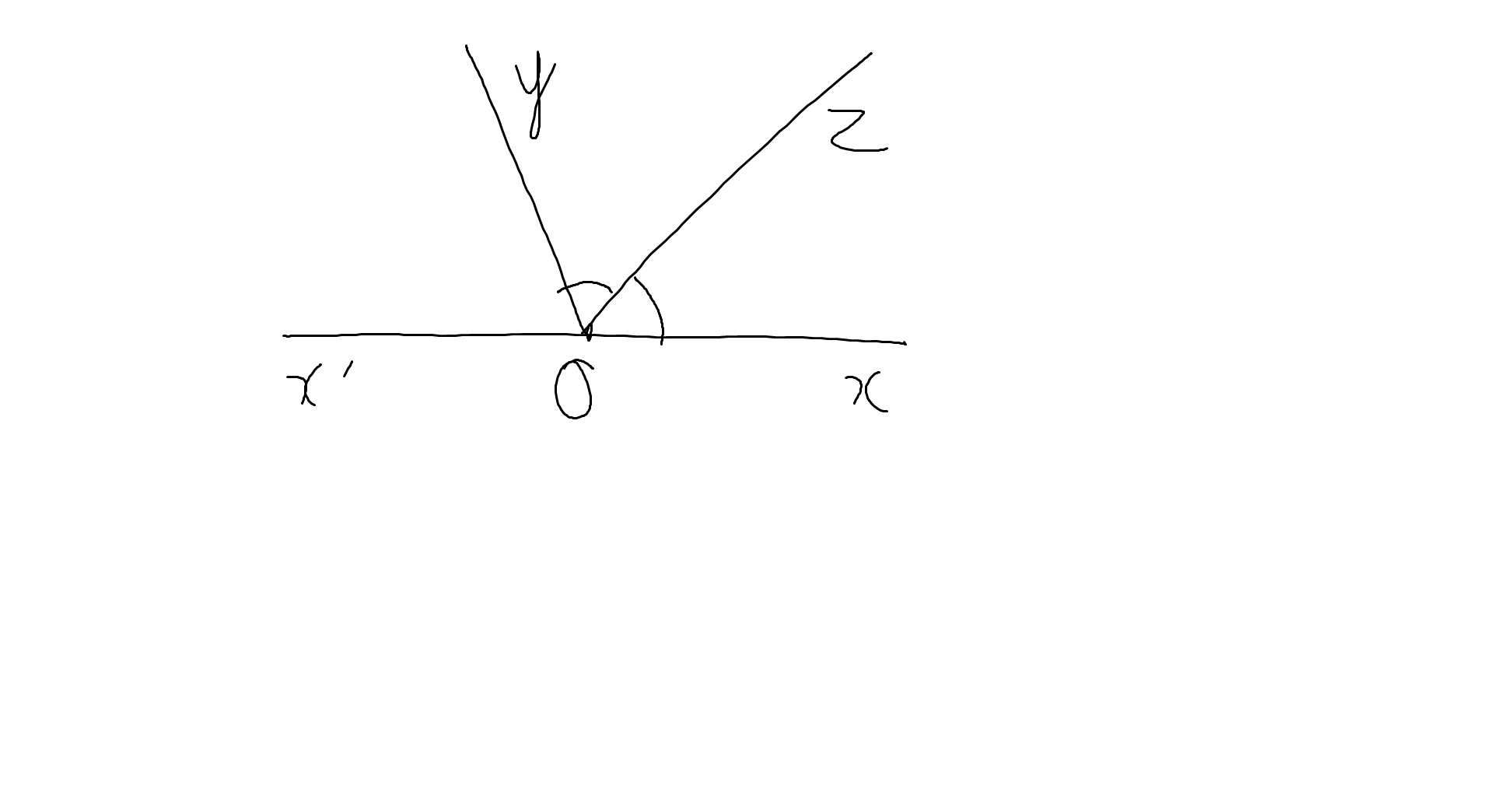
Oz là phân giác của góc xOy
=>\(\widehat{xOz}=\dfrac{\widehat{xOy}}{2}=\dfrac{142^0}{2}=71^0\)
Ta có: \(\widehat{xOz}+\widehat{x'Oz}=180^0\)(hai góc kề bù)
=>\(\widehat{x'Oz}=180^0-71^0=109^0\)


a: Ta có: ED\(\perp\)HF
GK\(\perp\)HF
Do đó: ED//GK
Xét ΔEDH vuông tại D và ΔGKF vuông tại K có
EH=GF
\(\widehat{EHD}=\widehat{GFK}\)(hai góc so le trong, EH//FG)
Do đó: ΔEDH=ΔGKF
=>ED=GK
Xét tứ giác EDGK có
ED//GK
ED=GK
Do đó: EDGK là hình bình hành
b: Ta có: EDGK là hình bình hành
=>EG cắt DK tại trung điểm của mỗi đường
mà O là trung điểm của DK
nên O là trung điểm của EG
Xét tứ giác EMGN có
EM//GN
EN//GM
Do đó: EMGN là hình bình hành
=>EG cắt MN tại trung điểm của mỗi đường(1)
mà O là trung điểm của EG
nên O là trung điểm của MN
c: Ta có: EHGF là hình bình hành
=>EG cắt HF tại trung điểm của mỗi đường(2)
Từ (1),(2) suy ra EG,MN,HF đồng quy

Đây là toán nâng cao chuyên đề lập số theo điều kiện cho trước. Cấu trúc thi chuyên, thi học sinh giỏi các cấp. Hôm nay, Olm sẽ hướng dẫn các em giải chi tiết dạng này bằng tư duy logic như sau:
Giải:
+ Vì Anthena nghĩ đến ba số từ 1 đến 10 nên ba số mà Anthen nghĩ đến là ba số khác nhau
+ Vì tích của ba số là 12 nên 12 chia hết cho cả ba số đó.
+ Mặt khác ta có: 1 x 2 x 6 = 12
1 x 3 x 4 = 12
và 1 < 2 < 3 < 4 < 6
Vậy số lớn nhất trong ba số là 6.
Đáp số: 6