chứng minh rằng tồn tại một bội của 2023 có dạng 202420242024...2024
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có: EF song song MN (cùng vuông góc AB)
D là trung điểm OA \(\Rightarrow AD=OD=\dfrac{R}{2}\)
Mà \(AC=OB=R\)
\(\Rightarrow AC+AD=OD+OB\Rightarrow DC=BD\)
Hay D là trung điểm BD
\(\Rightarrow EF\) là đường trung bình tam giác BMN
\(\Rightarrow MN=2EF\)
AB là đường kính và E thuộc đường tròn \(\Rightarrow\widehat{AEB}=90^0\) hay tam giác ABE vuông tại E
Áp dụng hệ thức lượng trong tam giác vuông ABE với đường cao ED:
\(ED^2=AD.DB=AD\left(OD+OB\right)=\dfrac{R}{2}.\left(\dfrac{R}{2}+R\right)=\dfrac{3R^2}{4}\)
\(\Rightarrow ED=\dfrac{R\sqrt{3}}{2}\)
\(\Rightarrow EF=2ED=R\sqrt{3}\)
\(\Rightarrow MN=2EF=2R\sqrt{3}\)
Gọi G là giao điểm của EF và AB. Ta có:
AG = AD + DG = R + R/2 = 3R/2
Vì tam giác ABC vuông tại C nên ta có:
AC^2 + BC^2 = AB^2
R^2 + BC^2 = (2R)^2
BC = R√3
Ta có:
CG = BC - BC/2 = R√3 - R√3/2 = R√3/2
Vì tam giác CGE vuông tại G nên ta có:
GE = CG * tan(∠GCE) = CG * tan(∠CBE)
GE = R√3/2 * tan(∠CBE)
Vì EF vuông góc với AB nên tam giác BEG vuông tại G, ta có:
BG^2 + GE^2 = BE^2
(R/2)^2 + (R√3/2 * tan(∠CBE))^2 = R^2
R^2/4 + 3R^2/4 * tan^2(∠CBE) = R^2
tan^2(∠CBE) = 1/3
tan(∠CBE) = √(1/3)
sin(∠CBE) = 1/√3
MN = 2 * GM = 2 * GE * sin(∠CBE)
MN = 2 * R√3/2 * √(1/3) = R
Vậy độ dài đoạn thẳng MN là R.

Để giải phép tính này, trước hết chúng ta cần thực hiện phép chia trước, sau đó thực hiện phép cộng. Dưới đây là cách giải:
- 5322,666744 : 5,333332 = 998
- 17443,478 : 0,993 = 17569
Sau đó, ta thực hiện phép cộng:
998 + 17569 = 18567
Vậy kết quả của phép tính là 18567 viết dưới dạng hỗn số.
Còn phần phân số đâu bạn.
Hỗn số có hai phần là: Số nguyên đứng trước dấu gạch ngang và phân số.

Tham khảo:
Gọi: số tiền loại 50000 đ là x ; số tiền loại 500000 đ là y
Ta có: x + y = 15 (1)
50000x + 200000y -30000= 1320000 (1)
Giải hai phương trình trên :
{x=11
y=4

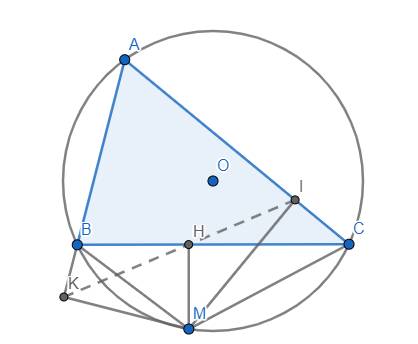
1, Ta có \(\widehat{MHB}=\widehat{MKB}=90^o\) nên tứ giác BHMK nội tiếp đường tròn (BM) nên \(\widehat{MHK}=\widehat{MBK}\)
Lại có tứ giác ABCM nội tiếp nên \(\widehat{MBK}=\widehat{ACM}\) (góc ngoài bằng góc trong đối)
\(\Rightarrow\widehat{MHK}=\widehat{MBK}=\widehat{ACM}\)
2, Ta có \(\widehat{MHC}=\widehat{MIC}=90^o\) nên tứ giác MHIC nội tiếp đường tròn (MC).
\(\Rightarrow\widehat{MHI}+\widehat{MCA}=180^o\)
Lại có \(\widehat{MCA}=\widehat{MHK}\left(cmt\right)\Rightarrow\) \(\widehat{MHI}+\widehat{MHK}=180^o\) \(\Rightarrow\) H, K, I thẳng hàng.
Thêm: Đường thẳng qua 3 điểm H, I, K gọi là đường thẳng Simson trong tam giác. Bạn có thể lên mạng tham khảo thêm.

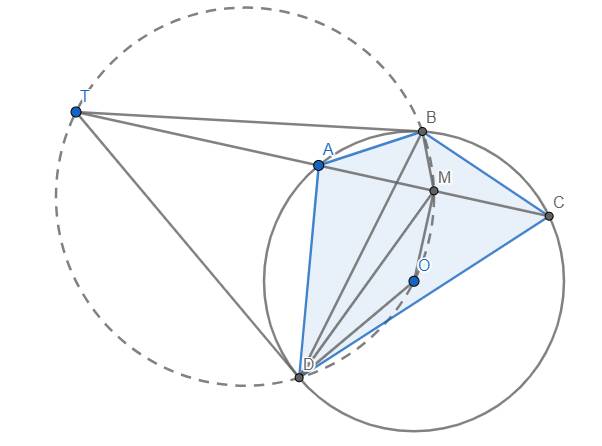
Gọi M là trung điểm của AC và T là điểm đồng quy của 2 tiếp tuyến tại B, D và đường thẳng AC.
Nhận thấy \(\widehat{OBT}=\widehat{ODT}=\widehat{OMT}=90^o\) nên 5 điểm O, M, B, T, D cùng thuộc đường tròn (OT).
Ta có \(\widehat{DCM}=\widehat{DCA}=\widehat{DBA}\)
Và \(\widehat{DMC}=180^o-\widehat{TMD}\) \(=180^o-\widehat{DBT}\) \(=180^o-\widehat{BCD}\) \(=\widehat{DAB}\)
Nên \(\Delta DAB\sim\Delta DMC\left(g.g\right)\)
\(\Rightarrow\dfrac{AB}{MC}=\dfrac{BD}{CD}\)
\(\Rightarrow AB.CD=MC.BD=\dfrac{1}{2}AC.BD\)
Tương tự, ta chứng minh được \(AD.BC=\dfrac{1}{2}AC.BD\) (hoặc cùng có thể dùng định lý Ptolemy trong tứ giác ngoại tiếp để suy ra điều này).
\(\Rightarrow AB.CD=AD.BC\left(=\dfrac{1}{2}AC.BD\right)\)
Ta có đpcm.
Mình trả lời rồi nhé bạn. Nếu bạn chưa xem được đáp án thì bạn vào trang cá nhân của mình xem nhé.

1) \(x^2-2x-15=0\)
\(\Delta=\left(-2\right)^2-4\cdot1\cdot-15=64>0\)
Phương trình có 2 nghiệm phân biệt
\(x_1=\dfrac{2+\sqrt{64}}{2\cdot1}=5\)
\(x_2=\dfrac{2-\sqrt{64}}{2\cdot1}=-3\)
2) \(x^2-2mx+m-2=0\)
\(\Delta=\left(-2m\right)^2-4\cdot1\cdot\left(m-2\right)=4m^2-4m+8=\left(2m-1\right)^2+7>0\forall m\)
Theo vi-ét:
\(\left\{{}\begin{matrix}x_1+x_2=\dfrac{-\left(-2m\right)}{1}=2m\\x_1x_2=\dfrac{m-2}{1}=m-2\end{matrix}\right.\)
Ta có: \(\left(3+x_1\right)\left(2-x_2\right)-\left(3+x_2\right)\left(x_1-2\right)=x^2_1+x^2_2+18\)
\(\Leftrightarrow6-3x_2+2x_1-x_1x_2-\left(-6+3x_1-2x_2+x_1x_2\right)=x^2_1+x^2_2+18\)
\(\Leftrightarrow6-3x_2+2x_1-x_1x_2+6-3x_1+2x_2-x_1x_2=\left(x_1+x_2\right)^2-2x_1x_2+18\)
\(\Leftrightarrow12-3\left(x_1+x_2\right)+2\left(x_1+x_2\right)-2x_1x_2=\left(x_1+x_2\right)^2-2x_1x_2+18\)
\(\Leftrightarrow12-\left(x_1+x_2\right)=\left(x_1+x_2\right)^2+18\)
\(\Leftrightarrow12-2m=\left(2m\right)^2+18\)
\(\Leftrightarrow12-2m=4m^2+18\)
\(\Leftrightarrow4m^2+2m+6=0\)
\(\Leftrightarrow m\in\varnothing\)
Vậy không có m thỏa mãn

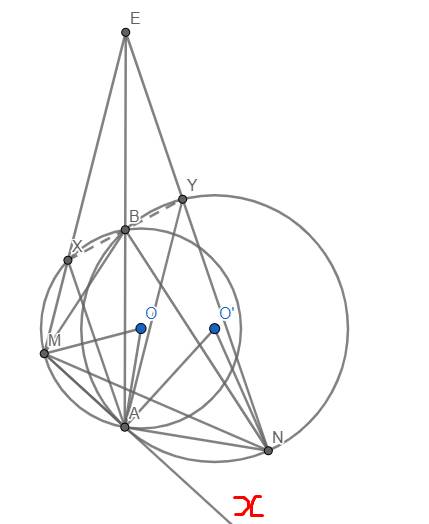
Gọi X và Y lần lượt là giao điểm thứ hai của EM với (O), EN với (O').
Ta có \(\widehat{MAO'}=\widehat{NAO}\left(=90^o\right)\) nên \(\widehat{MAO}=\widehat{NAO'}\). Hơn nữa tam giác MAO và NAO' đều là các tam giác cân nên \(\Rightarrow\widehat{MOA}=\widehat{NO'A}\)
Trong đường tròn (O), ta có: \(\widehat{MOA}=sđ\stackrel\frown{MA}=2.\dfrac{1}{2}sđ\stackrel\frown{MA}=2\widehat{MBA}\)
Tương tự, ta có \(\widehat{NO'A}=2\widehat{ABN}\)
\(\Rightarrow\widehat{MBA}=\widehat{ABN}\)
Hơn nữa có \(\widehat{MAB}=\widehat{ANB}\) (vì chúng lần lượt là góc tạo bởi tiếp tuyến và dây cung và góc nội tiếp cùng chắn cung nhỏ AB của (O').
\(\Rightarrow\Delta BAM\sim\Delta BNA\left(g.g\right)\)
\(\Rightarrow\dfrac{BA}{BN}=\dfrac{BM}{BA}\)
Do \(BA=BE\) nên \(\dfrac{BE}{BN}=\dfrac{BM}{BE}\)
Lại có \(\widehat{MBA}=\widehat{ABN}\left(cmt\right)\) \(\Rightarrow\widehat{EBM}=\widehat{EBN}\)
\(\Rightarrow\Delta MBE\sim\Delta EBN\left(c.g.c\right)\)
\(\Rightarrow\widehat{MEB}=\widehat{ENB}\)
Lại có \(\widehat{ENB}=\widehat{BNY}=\widehat{BAY}\) nên \(\widehat{MEB}=\widehat{BAY}\) \(\Rightarrow\) EX//AY
\(\Rightarrow\widehat{AYN}=\widehat{MEN}\)
Hơn nữa vì \(\widehat{NAx}=\widehat{AYN}\) (góc tạo bởi tiếp tuyến và dây cung và góc nội tiếp cùng chắn cung nhỏ AN trong (O'))
\(\Rightarrow\widehat{NAx}=\widehat{MEN}\)
Từ đó suy ra tứ giác AMEN nội tiếp (góc ngoài bằng góc trong đối)
Ta có đpcm.

A B C E F H M K D I
a/
E và F bình đẳng nhau nên tôi chỉ c/m ME là tiếp tuyến với đường tròn đường kính AH. Còn c/m MF là tiếp tuyến làm tương tự bạn tự c/m nhé
Gọi I là tâm đường tròng đường kính AH => IA=IH
Gọi D là giao của AH với BC
Xét tg ABC có \(AH\perp BC\) (trong tg 3 đường cao đồng quy)
\(\Rightarrow AD\perp BC\)
Xét tg vuông ADC và tg vuông BEC có
\(\widehat{DAC}=\widehat{EBC}\) (cùng phụ với \(\widehat{C}\) ) (1)
Xét tg vuông AHE có
\(IA=IH\Rightarrow IE=IA=IH=\dfrac{AH}{2}\) (trong tg vuông trung tuyến thuộc cạnh huyền bằng nửa cạnh huyền)
\(\Rightarrow E\in\left(I\right)\) và tg AIE cân tại I
\(\Rightarrow\widehat{DAC}=\widehat{AEI}\) (góc ở đáy tg cân) (2)
Xét tg vuông BEC có
\(MB=MC\left(gt\right)\Rightarrow ME=MB=MC=\dfrac{BC}{2}\) (trong tg vuông trung tuyến thuộc cạnh huyền bằng nửa cạnh huyền)
=> tg BME cân tại M
\(\Rightarrow\widehat{EBC}=\widehat{BEM}\) (góc ở đáy tg cân) (3)
Từ (1) (2) (3) \(\Rightarrow\widehat{AEI}=\widehat{BEM}\)
Mà \(\widehat{AEI}+\widehat{BEI}=\widehat{AEB}=90^o\)
\(\Rightarrow\widehat{BEM}+\widehat{BEI}=\widehat{MEI}=90^o\Rightarrow ME\perp IE\) => ME là tiếp tuyến với đường tròn đường kính AH
b/
Xét tg MEK và tg MAE có
\(\widehat{AME}\) chung
Ta có
\(sđ\widehat{MEK}=\dfrac{1}{2}sđcungEK\) (góc giữa tiếp tuyến và dây cung)
\(sđ\widehat{MAE}=\dfrac{1}{2}sđcungEK\) (góc nội tiếp (O))
\(\Rightarrow\widehat{MEK}=\widehat{MAE}\)
=> tg MEK đồng dạng với tg MAE (g.g.g)
\(\Rightarrow\dfrac{ME}{MA}=\dfrac{MK}{ME}\Rightarrow MK.MA=ME^2\)
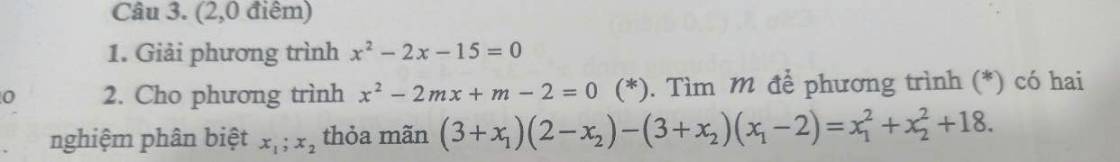
Xét 2024 số:
\(a_1=2024\)
\(a_2=20242024\)
\(a_3=202420242024\)
...
\(a_{2024}=20242024...2024\) (2024 lần cụm "2024")
Một số khi chia cho 2023 thì có 2023 số dư phân biệt là 0, 1, 2,..., 2023
\(\Rightarrow\) Theo nguyên lí Dirichlet tồn tại 2 số \(a_i,a_j\left(i\ne j,1\le i< j\le2024\right)\) trong số 2024 số kể trên có cùng số dư khi chia cho 2023.
\(\Rightarrow a_j-a_i⋮2023\)
\(\Rightarrow20242024...2024-20242024...2024⋮2023\)
(\(j\) cụm "2024) (\(i\) cụm "2024)
\(\Rightarrow20242024...2024000...00⋮2023\)
(\(j-i\) cụm "2024" và \(i\) chữ số 0)
\(\Rightarrow20242024...2024.10^i⋮2023\) (*)
Nhưng vì \(10^i=2^i.5^i\) và \(2023=7.17^2\) nên \(ƯCLN\left(10^i,2023\right)=1\)
Từ đó (*) suy ra \(20242024...2024⋮2023\)
(\(j-i\) cụm 2024)
Ta có đpcm.