a: Xét (O) có

ΔACB nội tiếp

AB là đường kính

Do đó: ΔACB vuông tại C

=>BC\(\perp\)AF tại C

Xét (O) có

ΔADB nội tiếp

AB là đường kính

Do đó: ΔADB vuông tại D

=>AD\(\perp\)FB tại D

Xét tứ giác FCED có \(\widehat{FCE}+\widehat{FDE}=90^0+90^0=180^0\)

nên FCED là tứ giác nội tiếp

=>F,E,D,C cùng thuộc một đường tròn

b: Xét (O) có \(\widehat{CAD}\) là góc nội tiếp chắn cung CD

nên \(\widehat{CAD}=\dfrac{\widehat{COD}}{2}=60^0\)

Ta có: ΔFDA vuông tại D

=>\(\widehat{DFA}+\widehat{DAF}=90^0\)

=>\(\widehat{DFC}=60^0\)

Xét ΔOCD có \(cosCOD=\dfrac{OC^2+OD^2-CD^2}{2\cdot OC\cdot OD}\)

=>\(\dfrac{R^2+R^2-CD^2}{2\cdot R\cdot R}=cos120=-\dfrac{1}{2}\)

=>\(CD=R\sqrt{3}\)

Xét ΔFCD có \(\dfrac{CD}{sinCFD}=2R_1\)

=>\(2R_1=\dfrac{R\sqrt{3}}{sin60}=R\sqrt{3}:\dfrac{\sqrt{3}}{2}=2R\)

=>\(R_1=R\)

=>Bán kính đường tròn ngoại tiếp tứ giác FCED là R

Sửa đề: \(x^2+2x+m-3=0\)

\(\text{Δ}=2^2-4\left(m-3\right)=4-4m+12=-4m+16\)

Để phương trình có hai nghiệm phân biệt thì -4m+16>0

=>-4m>-16

=>m<4

Theo Vi-et, ta có;

\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=-2\\x_1x_2=\dfrac{c}{a}=m-3\end{matrix}\right.\)

\(\left\{{}\begin{matrix}x_1=2x_2\\x_1+x_2=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3x_2=-2\\x_1=2x_2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_2=-\dfrac{2}{3}\\x_1=2\cdot\dfrac{-2}{3}=-\dfrac{4}{3}\end{matrix}\right.\)

\(x_1x_2=m-3\)

=>\(m-3=\left(-\dfrac{2}{3}\right)\cdot\left(-\dfrac{4}{3}\right)=\dfrac{8}{9}\)

=>\(m=3+\dfrac{8}{9}=\dfrac{35}{9}\)(nhận)

\(\sqrt[2]{5+6}=\sqrt{11}\)

bằng: 3.31662479

lời giải cô ơi =))

điền dấu cộng á

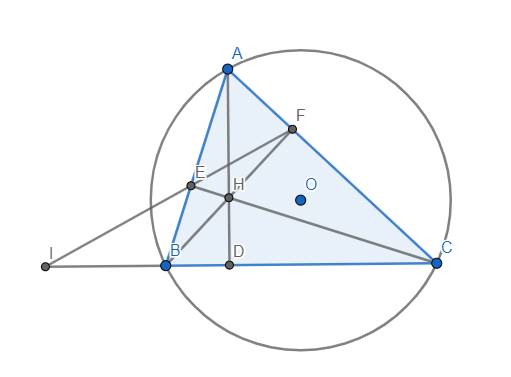
 a) Ta có \(\widehat{BEC}=\widehat{BFC}=90^o\) nên tứ giác BEFC nội tiếp đường tròn (BC).

 b) Tứ giác BEFC nội tiếp \(\Rightarrow\widehat{AEF}=\widehat{ACB}\)

Tam giác ABC và AFE có:

 \(\widehat{A}\) chung, \(\widehat{AEF}=\widehat{ACB}\)

 \(\Rightarrow\Delta ABC\sim\Delta AFE\left(g.g\right)\)

 \(\Rightarrow\dfrac{AB}{AF}=\dfrac{AC}{AE}\)

 \(\Rightarrow AB.AE=AF.AC\)

c) Áp dụng định lý Ceva cho tam giác ABC, ta được:

\(\dfrac{DB}{DC}.\dfrac{FC}{FA}.\dfrac{EA}{EB}=1\)      (1)

 Áp dụng định lý Menelaus cho tam giác ABC, cát tuyến FEI, ta có:

 \(\dfrac{IB}{IC}.\dfrac{FC}{FA}.\dfrac{EA}{EB}=1\)       (2)

 Từ (1) và (2), suy ra \(\dfrac{DB}{DC}=\dfrac{IB}{IC}\), ta có đpcm.

a: Xét tứ giác SAOB có \(\widehat{SAO}+\widehat{SBO}=90^0+90^0=180^0\)

nên SAOB là tứ giác nội tiếp

b:

Xét ΔSAO vuông tại A có \(SA^2+AO^2=SO^2\)

=>\(SA^2=8^2-4^2=48\)

=>\(SA=4\sqrt{3}\left(cm\right)\)

Xét ΔSAO vuông tại A có \(sinASO=\dfrac{AO}{OS}=\dfrac{1}{2}\)

nên \(\widehat{ASO}=30^0\)

Xét (O) có

SA,SB là các tiếp tuyến

Do đó: SO là phân giác của góc ASB và SA=SB

=>\(\widehat{ASB}=2\cdot\widehat{ASO}=60^0\)

Xét ΔSAB có SA=SB và \(\widehat{ASB}=60^0\)

nên ΔSAB đều

=>\(AB=SA=4\sqrt{3}\left(cm\right)\)