Gọi số áo mà tổ cần may theo kế hoạch là x(chiếc), x € N*

Vì ban đầu, tổ có ý định may 30 chiếc áo mỗi ngày nên thời gian dự định hoàn thành kế hoạch là x/30(ngày)

Thực tế tổ đã may thêm 20 chiếc áo nữa nên số áo tổ đã may được là x+20(chiếc)

Vì thực tế mỗi ngày may được 40 chiếc áo nên thời gian tổ đã may áo là x+20/40(ngày)

Vì tổ hoàn thành kế hoạch sớm hơn 3 ngày nên ta có phương trình:

x/30 - x+20/40=3

4x/120-3(x+20)/120=360/120

4x/120-3x+60/120=360/120

4x-(3x+60)=360

4x-3x-60=360

4x-3x=360+60

x=420(Thoả mãn điều kiện)

Vậy theo kế hoạch tổ cần may 420 chiếc áo 

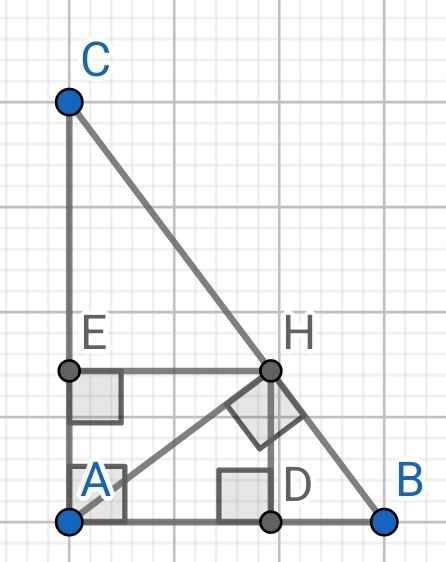
a) Xét hai tam giác vuông: ∆BDH và ∆BHA có:

∠B chung

⇒ ∆BDH ∽ ∆BHA (g-g)

b) Xét hai tam giác vuông: ∆AHB và ∆ADH có:

∠A chung

⇒ ∆AHB ∽ ∆ADH (g-g)

⇒ AH/AD = AB/AH

⇒ AH² = AD.AB

a) x = 2 A = (2 - 6)/(2 + 2) = -1

b) B = 6/(x - 2) + x/(x + 2) - 8/(x² - 4)

= [6(x + 2) + x(x - 2) - 8]/[(x - 2)(x + 2)]

= (6x + 12 + x² - 2x - 8)/[(x - 2)(x + 2)]

= (x² + 4x + 4)/[(x - 2)(x + 2)]

= (x + 2)²/[(x - 2)(x + 2)]

= (x + 2)/(x - 2)

c) P = A.B

= (x - 6)/(x + 2) . (x + 2)/(x - 2)

= (x - 6)/(x - 2)

Để P = 2/3 thì

(x - 6)/(x - 2) = 2/3

3(x - 6) = 2(x - 2)

3x - 18 = 2x - 4

3x - 2x = -4 + 18

x = 14

Vậy x = 14 thì P = 2/3

tại x = 1 , y = -3
x^2 - 4y^2/x -2y = 1^2 - 4.(-3)^2/1 -2.(-3) = 2 - 36 + 6 = -28

Đặt \(A=\dfrac{x^2-4y^2}{x-2y}\)

=>\(A=\dfrac{\left(x-2y\right)\left(x+2y\right)}{x-2y}=x+2y\)

Thay x=1 và y=-3 vào A, ta được:

\(A=1+2\cdot\left(-3\right)=1-6=-5\)

Thay x=1 và y=-3 vào phân thức \(\dfrac{x^2-y^2}{x-2y}\), ta được:

\(\dfrac{1^2-\left(-3\right)^2}{1-2\cdot\left(-3\right)}=\dfrac{1-9}{1+2\cdot3}=\dfrac{-8}{7}\)

ĐKXĐ: \(4x^2-1\ne0\)

=>\(x^2\ne\dfrac{1}{4}\)

=>\(x\notin\left\{\dfrac{1}{2};-\dfrac{1}{2}\right\}\)

a: Để (d) song song với đường thẳng y=-x+m thì

\(\left\{{}\begin{matrix}m-1=-1\\m\ne4\end{matrix}\right.\)

=>m=0

b: Thay x=1 và y=5 vào y=2x+b, ta được:

\(b+2\cdot1=5\)

=>b+2=5

=>b=3

Bài 1:

Gọi A là biến cố "Số xuất hiện trên quả bóng là số nguyên tố"

=>A={2;3;5;7;11}

=>n(A)=5

\(n\left(\Omega\right)=12-1+1=12\)

\(\Leftrightarrow P_A=\dfrac{5}{12}\)

\(4h25p=\dfrac{53}{12}\left(giờ\right)\)

Độ dài quãng đường từ nhà đến tỉnh là:

\(\dfrac{53}{12}\cdot14=\dfrac{371}{6}\left(km\right)\)