 lời giải kèm hình. giúp mik vs ạ mik sẽ kb ạ
lời giải kèm hình. giúp mik vs ạ mik sẽ kb ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


= -418-\(\left\{-218-\left[-118-200+2023\right]\right\}\)
= -418-\(\left\{-218-\left[-318+2023\right]\right\}\)
= -418-\(\left\{-218-1705\right\}\)
= -418--1923
=1505
- 418 - {218 - [-118 - (318) + 2023]}
= -418 - {218 - [-118 - 318 + 2023]}
= -418 - {218 - [- 436 + 2023]}
= - 418 - {218 - 1587}
= - 418 - (-1369)
= -418 + 1369
= 951

a: \(A=\dfrac{2x}{x+3}+\dfrac{x+1}{x-3}+\dfrac{3-11x}{9-x^2}\)
\(=\dfrac{2x}{x+3}+\dfrac{x+1}{x-3}+\dfrac{11x-3}{\left(x-3\right)\left(x+3\right)}\)
\(=\dfrac{2x\left(x-3\right)+\left(x+1\right)\left(x+3\right)+11x-3}{\left(x-3\right)\left(x+3\right)}\)
\(=\dfrac{2x^2-6x+x^2+4x+3+11x-3}{\left(x-3\right)\left(x+3\right)}=\dfrac{3x^2+9x}{\left(x-3\right)\left(x+3\right)}=\dfrac{3x}{x-3}\)
b: Thay x=5 vào A, ta được:
\(A=\dfrac{3\cdot5}{5-3}=\dfrac{15}{2}\)

a; (135 - 35).(-37) + 37.(- 42 - 58)
= 100.(-37) + 37.(-100)
= - 100.(37+ 37)
= -100. 74
= - 7400
b; - 65.(87 - 17) - 87.(17 - 65)
= - 65.87 + 65.17 - 87.17 + 87.65
= (-65.87 + 87.65) - (87.17 - 65.17)
= 0 + 17.(87- 65)
= 17.(-22)
= - 374
c; [3.(-2) - (-8)]. (-7 - (-2).(-5))
= [-6 + 8].(-7 - 10)
= 2.(-17)
= - 34
d; 39.(-12) + (-39) + (117).29
= - 39.(12 + 1) + 3393
= -39.13 + 3393
= - 507 + 3393
= 2886
e; 63.(-71 - 55) - 71.(-55 - 63)
= -63.71 - 63.55 + 71.55 + 71.63
= (63.71 - 63.71) + (71.55 - 63.55)
= 0 + 55.(71 - 63)
= 55.8
= 440

a: \(2x\left(x-3y\right)-25\left(3y-x\right)\)
\(=2x\left(x-3y\right)+25\left(x-3y\right)\)
\(=\left(x-3y\right)\left(2x+25\right)\)
b: \(36x^2-24x+4\)
\(=4\left(9x^2-6x+1\right)\)
\(=4\left[\left(3x\right)^2-2\cdot3x\cdot1+1^2\right]\)
\(=4\left(3x-1\right)^2\)
c: \(\left(3x+2\right)^2+2\left(3x+2\right)\left(3x-1\right)+\left(3x-1\right)^2\)
\(=\left(3x+2+3x-1\right)^2\)
\(=\left(6x+1\right)^2\)

a: Xét ΔMAC và ΔMEB có
MA=ME
\(\widehat{AMC}=\widehat{EMB}\)(hai góc đối đỉnh)
MC=MB
Do đó: ΔMAC=ΔMEB
=>\(\widehat{MAC}=\widehat{MEB}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AC//EB
b: Xét ΔMAI và ΔMEK có
MA=ME
\(\widehat{MAI}=\widehat{MEK}\)(cmt)
AI=EK
Do đó: ΔMAI=ΔMEK
=>\(\widehat{AMI}=\widehat{EMK}\)
=>\(\widehat{EMK}+\widehat{EMI}=180^0\)
=>I,M,K thẳng hàng

S A B C D E F I K M
a/
Trong mp(SAC) Gọi K là giao của EF và AC
\(K\in EF\)
\(K\in AC;AC\in\left(ABC\right)\Rightarrow K\in\left(ABC\right)\)
=> K là giao của EF với (ABC)
b/
Trong mp (SBC), Gọi M là giao của SI với BF
\(M\in SI;SI\in\left(SAI\right)\Rightarrow M\in\left(SAI\right)\)
\(M\in BF;BF\in\left(ABF\right)\Rightarrow M\in\left(ABF\right)\)
\(A\in\left(SAI\right);A\in\left(ABF\right)\)
=> AM là giao tuyến giữa (SAI) và (ABF)
c/
\(I\in\left(SAI\right)\)
\(I\in BC;BC\in\left(BCE\right)\Rightarrow I\in\left(BCE\right)\)
\(E\in SA;SA\in\left(SAI\right)\Rightarrow E\in\left(SAI\right)\)
\(E\in\left(BCE\right)\)
=> IE là giao tuyến giữa (SAI) và (BCE)

a; (135 - 35).(-37) + 37.(- 42 - 58)
= 100.(-37) + 37.(-100)
= - 100.(37+ 37)
= -100. 74
= - 7400
b; - 65.(87 - 17) - 87.(17 - 65)
= - 65.87 + 65.17 - 87.17 + 87.65
= (-65.87 + 87.65) - (87.17 - 65.17)
= 0 + 17.(87- 65)
= 17.(-22)
= - 374
c; [3.(-2) - (-8)]. (-7 - (-2).(-5))
= [-6 + 8].(-7 - 10)
= 2.(-17)
= - 34
d; 39.(-12) + (-39) + (117).29
= - 39.(12 + 1) + 3393
= -39.13 + 3393
= - 507 + 3393
= 2886
e; 63.(-71 - 55) - 71.(-55 - 63)
= -63.71 - 63.55 + 71.55 + 71.63
= (63.71 - 63.71) + (71.55 - 63.55)
= 0 + 55.(71 - 63)
= 55.8
= 440

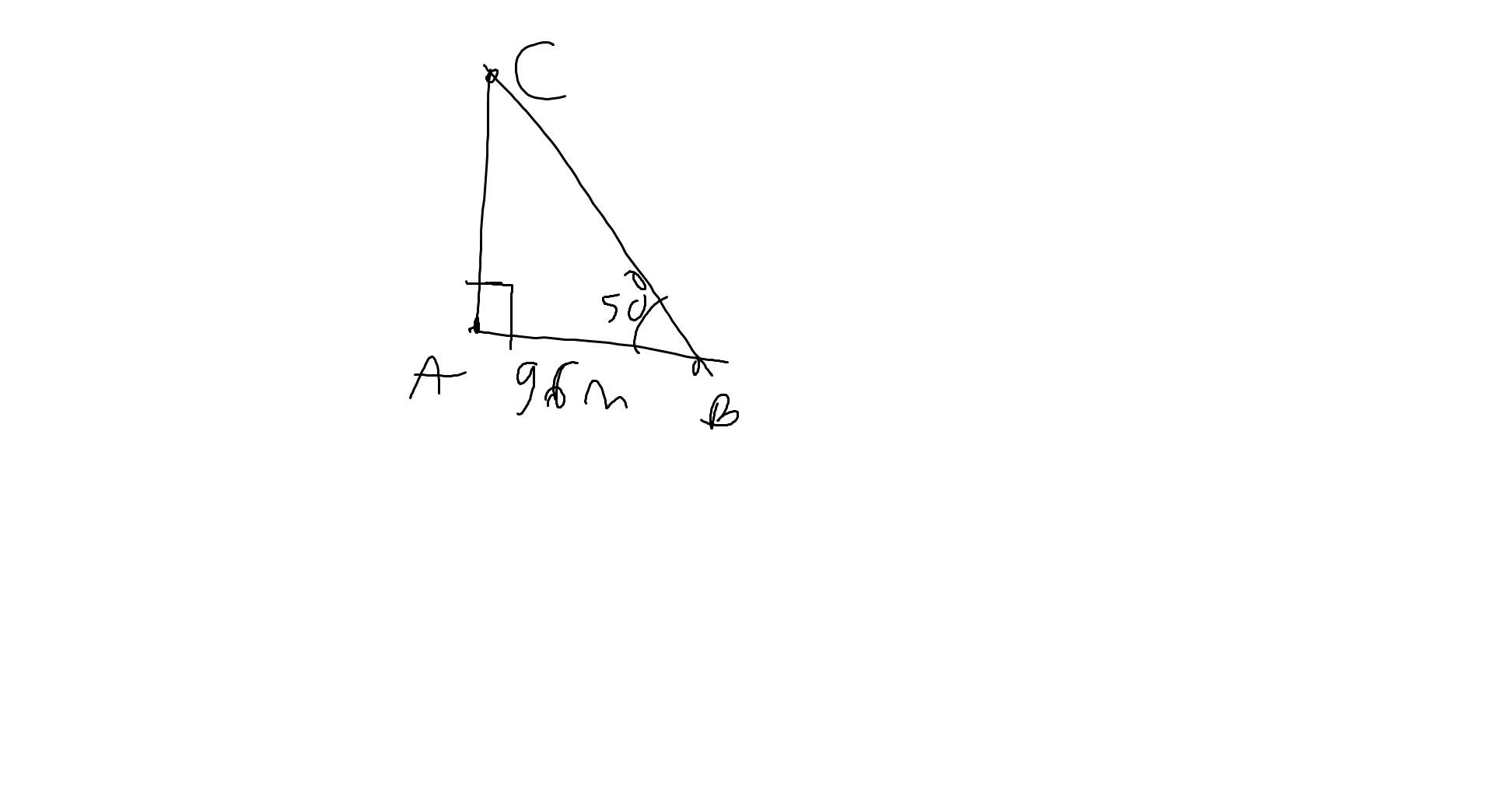
Gọi AB là bóng của cây trên mặt đất, AC là chiều cao của cây
Theo đề, ta có: AB\(\perp\)AC tại A, AB=96m; \(\widehat{B}=50^0\)
Xét ΔABC vuông tại A có \(tanB=\dfrac{AC}{AB}\)
=>\(AC=AB\cdot tanB=96\cdot tan50\simeq114,4\left(m\right)\)

mik thì 11/11 mí thi mik nghĩ bn phải chăm chỉ ôn luyện thôi dạng chính là rơi vào ước chung,ước,ước chung lớn nhất và bội,bội chung ,bội chung nhỏ nhất đó là đối với những bài toán đố thôi à mik chỉ biết vậy à
CHÚC BN THI TOT NGHE
a: Xét ΔABC và ΔCDA có
AB=CD
AC chung
BC=DA
Do đó: ΔABC=ΔCDA
=>\(\widehat{BAC}=\widehat{DCA}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AB//CD
b: ΔABC=ΔCDA
=>\(\widehat{ACB}=\widehat{DAC}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AD//BC
mà AH\(\perp\)BC
nên AH\(\perp\)AD