\(\frac{1}{2\left(x-1\right)}+\frac{3}{x^2-1}=\frac{1}{4}\)ĐK : \(x\ne\pm1\)

\(\Leftrightarrow\frac{2\left(x+1\right)+12}{4\left(x-1\right)\left(x+1\right)}=\frac{x^2-1}{4\left(x-1\right)\left(x+1\right)}\)

\(\Rightarrow2x+14=x^2-1\Leftrightarrow x^2-2x-15=0\)

\(\Delta=4-4\left(-15\right)=4+60=64\)

\(x_1=\frac{2-8}{2}=-3;x_2=\frac{2+8}{2}=5\)(tm)

Vậy tập nghiệm của pt là S = { -3 ; 5 } 

Là sai

là sai

Cậu kiểm tra lại xem có đúng không giúp mình nhé:

\(\sqrt{3}-x=x^2-\left(\sqrt{3}+x\right)\)

\(\Leftrightarrow\sqrt{3}-x+\sqrt{3}+x=x^2\)

\(\Leftrightarrow2\sqrt{3}=x^2\)

\(\Leftrightarrow x^4=\left(2\sqrt{3}\right)^2\)

\(\Leftrightarrow x^{4^{ }}=12\)

\(\Leftrightarrow x=\sqrt[4]{12}\)

!@#$%^&*())((*&^%$#@!omg WTF

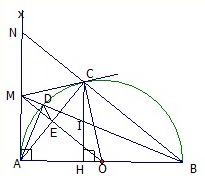
a/ Xét tg vuông ABK và tg vuông CDK có

\(\widehat{AKB}=\widehat{CKD}=90^o\)

\(\widehat{BAD}=\widehat{DCB}\) (góc nội tiếp đường tròn cùng chắn cung BD)

=> tg ABK đồng dạng với tg CDK \(\Rightarrow\frac{KA}{KC}=\frac{KB}{KD}\Rightarrow KA.KD=KB.KC\)

b/ Nối CH cắt AB tại I

Xét tg CDH có

\(CK\perp DH\) (đề bài) => CK là đường cao

\(KH=KD\) (đề bài) => CK là đường trung tuyến

=> tg CDH cân tại C (tg có đường cao đồng thời là đường trung tuyến => tg đó là tg cân)

\(\Rightarrow\widehat{KCD}=\widehat{KCH}\) (trong tg cân đường cao đồng thời là đường phân giác) (1)

\(\widehat{ABC}=\widehat{ADC}\) (góc nội tiếp cùng chắn cung AC) (2)

Xét tg vuông CKD có \(\widehat{KCD}+\widehat{ADC}=90^o\) (3)

Từ (1) (2) (3) => \(\widehat{KCH}+\widehat{ABC}=90^o\Rightarrow\widehat{BIC}=90^o\Rightarrow CH\perp AB\)

Mà \(AH\perp BC\)

=> H là trực tâm của tg ABC

c/

Ta có tg ADE là tg nội tiếp đường tròn (O)

Ta có 

\(BC\perp AD\) 

DE//BC

\(\Rightarrow DE\perp AD\Rightarrow\widehat{ADE}=90^0\) => AE là đường kính đường tròn (O) => DE đi qua O => A; O; E thẳng hàng

c, thiếu đề rồi phải có tọa đọ B nữa chứ ? 

a, \(\left(2\sqrt{44}-3\sqrt{77}\right):\sqrt{11}+\sqrt{63}\)

\(=\frac{\left(4\sqrt{11}-3\sqrt{7}\sqrt{11}\right)}{\sqrt{11}}+3\sqrt{7}\)

\(=4-3\sqrt{7}+3\sqrt{7}=4\)

b,Ta có :  \(\left(\frac{1}{\sqrt{x}-3}-\frac{1}{\sqrt{x}+3}\right).\frac{x-9}{6}\)

\(=\frac{\sqrt{x}+3-\sqrt{x}+6}{x-9}.\frac{x-9}{6}=\frac{9}{6}=\frac{3}{2}\)

sửa ý b, bấm nhầm 

\(\left(\frac{1}{\sqrt{x}-3}-\frac{1}{\sqrt{x}+3}\right).\frac{x-9}{6}\)

\(=\frac{\sqrt{x}+3-\sqrt{x}+3}{x-9}.\frac{x-9}{6}=\frac{6}{6}=1\)( đpcm )

 ta có hình sau :