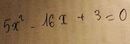a) Vì \(\hept{\begin{cases}MI\perp AB\\MK\perp AC\end{cases}\Rightarrow\hept{\begin{cases}\widehat{AIM}=90^0\\\widehat{AKM}=90^0\end{cases}}}\)

Xét tứ giác AIMK có \(\widehat{AIM}+\widehat{AKM}=180^0\)mà 2 góc này ở vị trí đối nhau trong tứ giác AIMK

\(\Rightarrow AIMK\)nội tiếp ( dhnb )

b)  Vì \(MP\perp BC\Rightarrow\widehat{MPC}=90^0\)

Xét tứ giác MPCK có \(\widehat{MPC}+\widehat{MKC}=180^0\)

Mà 2 góc này ở vị trí đối nhau trong tứ giác MPCK

\(\Rightarrow MPCK\)nội tiếp ( dhnb)

\(\Rightarrow\widehat{MPK}=\widehat{MCK}\)(1)

Vì AC là tiếp tuyến của (O) tại C; BC là dây cung

\(\Rightarrow\widehat{MCK}=\widehat{MBC}\left(=\frac{1}{2}sđ\widebat{MC}\right)\)(2)

Từ (1) và (2) \(\Rightarrow\widehat{MPK}=\widehat{MBC}\)

Thanks bạn

\(5x^2-16x+3=0\)

\(\Delta=16^2-4.3.5=196>0\)

\(\Rightarrow\)pt có 2 nghiệm pb \(\orbr{\begin{cases}x=\frac{16+\sqrt{196}}{10}=3\\x=\frac{16-\sqrt{196}}{10}\frac{1}{5}\end{cases}}\)

Vậy pt có tập nghiệm \(S=\left\{3;\frac{1}{5}\right\}\)

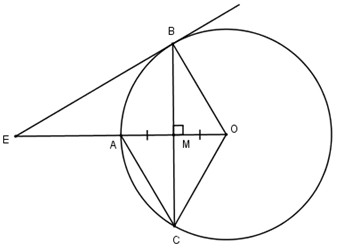
\(a,\) Tứ giác \(OCAB\)l là hình thoi.

Ta có: \(OA\perp OB\)\(\Rightarrow\)\(MB=MC\)

mà \(MA=MO\)nên tứ giác \(OCAB\)là hình bình hành.

Hình bình hành này có hai đường chéo vuông góc nên là hình thoi.

\(b,\) Ta có: \(BA=BO\) ( hai cạnh hình thoi ) \(BO=OA\)( bán kính tam giác ) nên tam giác \(ABO\)là tam giác đều.

\(\Rightarrow\)\(\widehat{BOA}=60^o\)

Ta có \(EB\)là tiếp tuyến \(\Rightarrow\)\(EB\perp OB\)

Xét tam giác \(BOE\)vuông tại \(B,\)có: 

\(BE=BO.tg60^o=R.tg60^o=R\sqrt{3}\)

a) Bán kính $OA$ vuông góc với dây $BC$ nên

$MB=MC$

Tứ giác $OCAB$ là hình bình hành (vì $MO=MA$, $MB=MC$), lại có $OA\perp BC$ nên tứ giác đó là hình thoi.

b) BE=Căn 3 x R

Đi chơi nãy giờ bây giờ mới được on ! Mệt quá ~

(~3~)

gio moi co nguoi tra loi

Áp dụng BĐT cô si ta có:

\(\frac{a}{18}+\frac{b}{24}+\frac{2}{ab}\ge3\sqrt[3]{\frac{ab}{18.24}.\frac{2}{ab}}=\frac{1}{2}\)

\(\frac{a}{9}+\frac{c}{6}+\frac{2}{ca}\ge1\) ( chỗ này mình làm tắt vì nó giống cái trên thôi ) 

\(\frac{b}{16}+\frac{c}{8}+\frac{2}{bc}\ge\frac{3}{4}\)

\(\frac{a}{9}+\frac{c}{6}+\frac{b}{12}+\frac{8}{abc}\ge4\sqrt[4]{\frac{8abc}{9.6.12abc}}=\frac{4}{3}\)

\(\frac{13a}{18}+\frac{13b}{24}\ge2\sqrt{\frac{13.13ab}{18.24}}\ge2\sqrt{\frac{13.13.12}{18.24}}=\frac{13}{3}\)

\(\frac{13b}{48}+\frac{13c}{24}\ge2\sqrt{\frac{13.13bc}{48.24}}\ge2\sqrt{\frac{13.13.8}{48.24}}=\frac{13}{6}\)

ấy chết lỡ tay bấm trả lời :))

làm típ:

Cộng từng vế :

\(\Rightarrow\left(a+b+c\right)+2\left(\frac{1}{ab}+\frac{1}{bc}+\frac{1}{ca}\right)+\frac{8}{abc}\ge\frac{121}{12}\)

Dấu "="xảy ra \(\Leftrightarrow\hept{\begin{cases}a=3\\b=4\\c=2\end{cases}}\)