chứng minh rằng A=2+22+23+...+22024 chia hết cho 10
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


3n + 4 ⋮ n
4 ⋮ n
n \(\in\) Ư(4) = {-4; -2; -1; 1; 2; 4}
n \(\in\) N nên n \(\in\) {1; 2; 4}
Vậy n \(\in\) {1; 2; 4}

S A B C D O M N d I P
a/ Qua S dựng đường thẳng d//AD
d//AD; \(S\in\left(SAD\right)\Rightarrow d\in\left(SAD\right)\)
d//AD;AD//BC => d//BC mà \(S\in\left(SBC\right)\Rightarrow d\in\left(SBC\right)\)
=> d chính là giao tuyến của (SAD) và (SBC)
b/
Trong (SAC) gọi I là giao của AM với SO
\(I\in SO;SO\in\left(SBD\right)\Rightarrow I\in\left(SBD\right)\)
=> I là giao của AM với (SBD)
Ta có BC//AD \(\Rightarrow\dfrac{OC}{OA}=\dfrac{BC}{AD}=\dfrac{1}{2}\)
2 tg SAM và tg CAM có chung đường cao từ A->SC và MS=MC nên \(S_{SAM}=S_{CAM}=S\)
2 tg AMO và tg CMO có chung đường cao từ M->AC nên
\(\dfrac{S_{AMO}}{S_{CMO}}=\dfrac{OA}{OC}=2\Rightarrow\dfrac{S_{AMO}}{2}=S_{CMO}=\dfrac{S_{AMO}+S_{CMO}}{2+1}=\dfrac{S_{CAM}}{3}\)
\(\Rightarrow\dfrac{S_{AMO}}{S_{CAM}}=\dfrac{S_{AMO}}{S_{SAM}}=\dfrac{2}{3}\)
2 tg AMO và tg SAM có chung AM nên
\(\dfrac{S_{AMO}}{S_{SAM}}=\) đường cao từ O->AM/đường cao từ S->AM \(=\dfrac{2}{3}\)
2 tg OMI và tg SMI có chung IM nên
\(\dfrac{S_{OMI}}{S_{SMI}}=\)đường cao từ O->AM/đường cao từ S->AM\(=\dfrac{2}{3}\)
2tg OMI và tg SMI có chung đường cao từ M->SO nên
\(\dfrac{S_{OMI}}{S_{SMI}}=\dfrac{OI}{SI}=\dfrac{2}{3}\)
\(\Rightarrow\dfrac{OI}{2}=\dfrac{SI}{3}=\dfrac{OI+SI}{2+3}=\dfrac{SO}{5}\Rightarrow\dfrac{SI}{SO}=\dfrac{3}{5}\)
c/
Gọi P là trung điểm của SA, Xét tg SAD có
PA=PS; ND=NS (gt) => PN là đường trung bình của tg SAD
=> PN//AD và \(PN=\dfrac{1}{2}AD\)
Ta có
PN//AD; AD//BC => PN//BC
\(AD=2BC\Rightarrow BC=\dfrac{1}{2}AD\)
=> PN//BC và \(PN=BC=\dfrac{1}{2}AD\)
=> BCNP là hbh (Tứ giác có 1 cặp cạnh đối // và bằng nhau là hbh)
=> CN//BP (cạnh đối hbh) mà \(BP\in\left(SAB\right)\) => CN//(SAB)
a.
Qua S kẻ đường thẳng d song song AD và BC
Do \(\left\{{}\begin{matrix}S\in\left(SAD\right)\\S\in d\\d||AD\end{matrix}\right.\) \(\Rightarrow d\in\left(SAD\right)\)
\(\left\{{}\begin{matrix}S\in\left(SBC\right)\\S\in d\\d||BC\end{matrix}\right.\) \(\Rightarrow d\in\left(SBC\right)\)
\(\Rightarrow d=\left(SAD\right)\cap\left(SBC\right)\)
b.
Trong mp (SAC), nối AM cắt SO tại I
\(\left\{{}\begin{matrix}O\in BD\in\left(SBD\right)\\S\in\left(SBD\right)\end{matrix}\right.\) \(\Rightarrow SO\in\left(SBD\right)\)
\(I\in SO\Rightarrow I\in\left(SBD\right)\)
\(\Rightarrow I=AM\cap\left(SBD\right)\)
Do AD song song BC, áp dụng định lý Thales:
\(\dfrac{OA}{OC}=\dfrac{AD}{BC}=2\) \(\Rightarrow OA=2OC=2\left(AC-OA\right)\Rightarrow\dfrac{OA}{AC}=\dfrac{2}{3}\)
Áp dụng định lý Menelaus:
\(\dfrac{OA}{AC}.\dfrac{CM}{MS}.\dfrac{SI}{IO}=1\Leftrightarrow\dfrac{2}{3}.1.\dfrac{SI}{IO}=1\)
\(\Rightarrow2SI=3IO=3\left(SO-SI\right)\)
\(\Rightarrow5SI=3SO\Rightarrow\dfrac{SO}{SI}=\dfrac{3}{5}\)

Do trong nhà chỉ có bóng xanh và bóng đỏ nên nếu không tính bóng xanh thì có 35 quả vậy bóng đỏ là 35 quả.
Nếu không tính bỏng đỏ thì có 42 quả vậy bóng xanh là 42 quả
Trong nhà có tất cả số quả bóng là: 42+ 35 = 77 (quả)
Đáp số: 77 quả

8 + 12 + \(x\) ⋮ 2
Vì 8; 12 ⋮ 2 ⇒ \(x\) ⋮ 2 ⇒ \(x\) \(\in\) B(2) ⇒ \(x=2k\) (k \(\in\) Z)

Giải
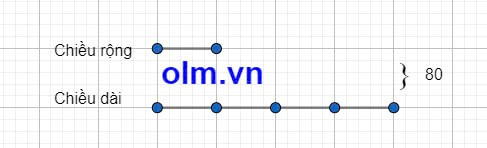
Ta có sơ đồ:
Theo sơ đồ ta có:
Chiều dài của mảnh đất: 80 : (1 + 4) x 4 = 64 (m)
Chiều rộng của mảnh đất là: 80 - 64 = 16 (m)
Diện tích của mảnh đất là: 64 x 16 = 1024 (m2)
Đáp số: 1024 m2

Đây là toán nâng cao chuyên đề tổng tỉ, ẩn tỉ, cấu trúc thi chuyên thi học sinh giỏi các cấp. Hôm nay, Olm sẽ hướng dẫn các em giải chi tiết dạng này như sau:
Giải:
Vì cứ 2 luống xà lách có 3 luống tỏi nên tỉ số số luống xà lách và số luống tỏi là:
2 : 3 = \(\dfrac{2}{3}\)
Ta có sơ đồ:
Theo sơ đồ ta có:
số luống tỏi là: 65 : (2+ 3) x 3 = 39 (luống)
Số luống xà lách là: 65 - 45 = 26 (luống)
Đáp số: 39 luống tỏi, 26 luống xà lách

a: 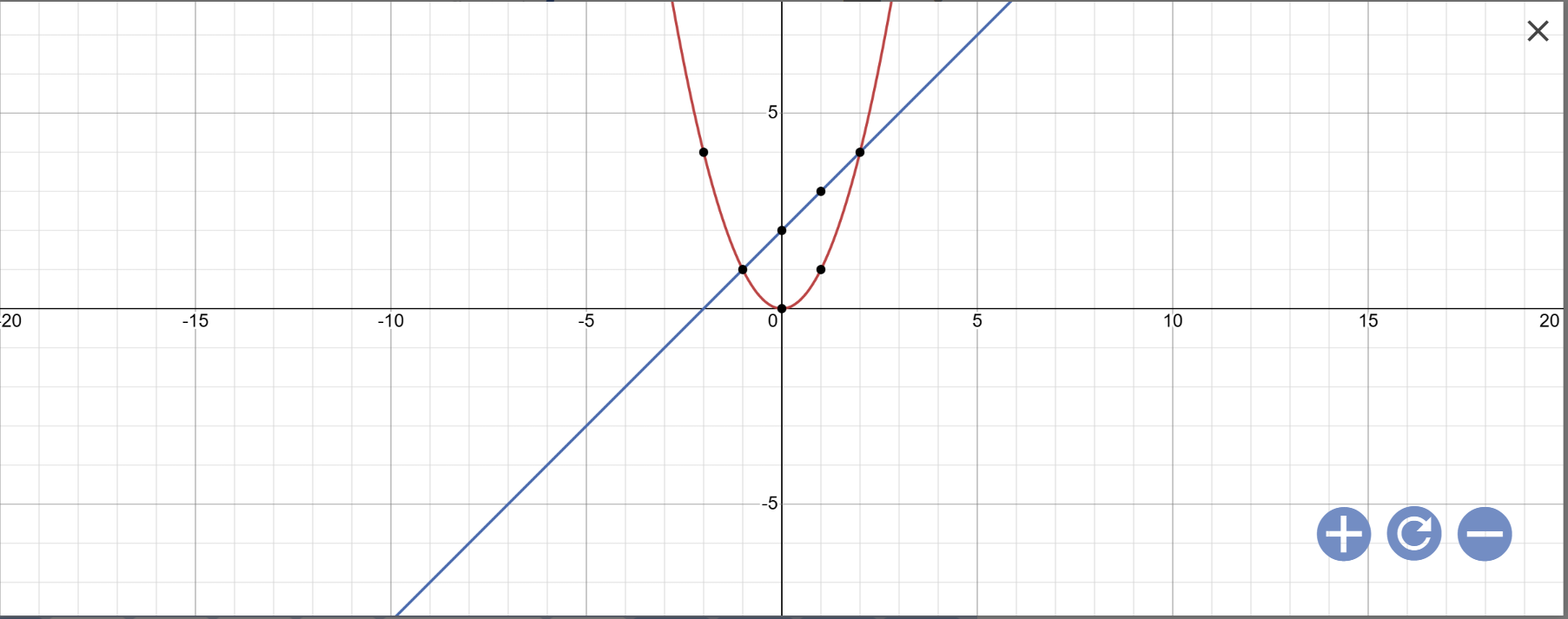
b: Phương trình hoành độ giao điểm là:
\(x^2=x+2\)
=>\(x^2-x-2=0\)
=>(x-2)(x+1)=0
=>\(\left[{}\begin{matrix}x-2=0\\x+1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-1\end{matrix}\right.\)
Khi x=2 thì y=x+2=2+2=4
Khi x=-1 thì y=-1+2=1
vậy: Tọa độ giao điểm của (P) và (d) là A(2;4); B(-1;1)
c: A,B là tọa độ các giao điểm của (d) và (P)
=>A(2;4); B(-1;1)
O(0;0); A(2;4); B(-1;1)
\(OA=\sqrt{\left(2-0\right)^2+\left(4-0\right)^2}=2\sqrt{5}\)
\(OB=\sqrt{\left(-1-0\right)^2+\left(1-0\right)^2}=\sqrt{2}\)
\(AB=\sqrt{\left(-1-2\right)^2+\left(1-4\right)^2}=3\sqrt{2}\)
Xét ΔOAB có \(BO^2+BA^2=OA^2\)
nên ΔBOA vuông tại B
=>\(S_{BOA}=\dfrac{1}{2}\cdot BA\cdot BO=\dfrac{1}{2}\cdot3\sqrt{2}\cdot\sqrt{2}=3\)

Đây là toán nâng cao chuyên đề bài toán về công việc, cấu trúc thi chuyên, thi học sinh giỏi các cấp. Hôm nay, Olm sẽ hướng dẫn các em giải chi tiết dạng này bằng phương pháp rút về đơn vị như sau:
Giải:
Cứ một ngày một người làm được: 1 : 12 : 18 = \(\dfrac{1}{216}\) (công việc)
Cứ chín ngày một người làm được: \(\dfrac{1}{216}\) x 9 = \(\dfrac{1}{24}\) (công việc)
Để hoàn thành công việc đó trong chín ngày cần số người là:
1 : \(\dfrac{1}{24}\) = 24 (người)
Để hoàn thành công việc trong chín ngày cần bổ sung số người là:
24 - 17 = 7 (người)
Đáp số: 17 người



Ai giúp tui vs
A = 2 + 22 + 23 + .. + 22024
A = 21 + 22 + 23 + ... + 22024
Xét dãy số 1; 2; 3; ...; 2024, đây là dãy số cách đều với khoảng cách là: 2 - 1= 1
Số số hạng của dãy số là: (2024 - 1) : 1+ 1 = 2024
Vì 2024 : 4 = 506
Vậy nhóm 4 số hạng liên tiếp của A vào nhau ta được:
A = (2 + 22 + 23 + 24) + .. + (22021+ 22022 + 22023 + 22024)
A = (2 + 22 + 23 + 24) + ... + 22020.(2 + 22 + 23 + 24)
A = (2 + 22 + 23 + 24).(20 + ... + 22020)
A = (2+ 4 +8+ 16).(20 + ... + 22020)
A = 30.(20 + ...+ 22020) = 10.3.(20+ ...+ 22020) ⋮ 10 (đpcm)