Một người có 3 viên đạn. Người đó bắn lần lượt từng viên vào bia cho đến khi hết đạn, xác suất bắn trúng mỗi viên là 0,7. Gọi X là số viên đạn bắn trúng bia. F(x) là hàm phân phối xác suất của X. Tính F(2, 5)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
HV
Hà Việt Anh
VIP
2 tháng 5
Xe may xuất phát chậm hơn ô tô và xe đạp là:
6 giờ 45 phút -6 giờ =45 phút=0,75 giờ
Trong 1 giờ ô tô và xe đạp đi được số km là:
15+45=60(km)
Để xe máy đi ở chính giữa ô tô và xe đạp thì xe máy đi được số km là
60:2=30(km)
Thời gian để xe máy đi chính giữa ô tô và xe đạp là:
0,75:(35-30)=0,15 giờ=9 phút
Trên quãng đường AB xe máy đi giữa ô tô và xe đạp lúc:
6 giờ 45 phút+9 phút=6 giờ 54 phút
Đáp số:6 giờ 54 phút
T
2 tháng 5
$\frac59+\frac27+\frac49+\frac57+\frac{7}{12}$
$=(\frac59+\frac49)+(\frac27+\frac57)+\frac{7}{12}$
$=1+1+\frac{7}{12}$
$=2+\frac{7}{12}=\frac{31}{12}$
$---$
4 giờ 15 phút + 2 giờ 17 phút + 3 giờ 45 phút + 1 giờ 43 phút
= (4 giờ 15 phút + 3 giờ 45 phút) + (2 giờ 17 phút + 1 giờ 43 phút)
= 7 giờ 60 phút + 3 giờ 60 phút
= 8 giờ + 4 giờ = 12 giờ
$---$
$9,05\times12,7+9,05\times97,8-9,05\times10,5$
$=9,05\times(12,7+97,8-10,5)$
$=9,05\times(110,5-10,5)$
$=9,05\times100=905$
CN
3
2 tháng 5
-Có 5 chất đó là:Chất đạm,Carbohy,Dratate,Chất béo,Vitamin và khoáng chất.
Đúng cho mình nha!!
PT
Phạm Thuỳ Chi
VIP
2 tháng 5
Chất bột đường, chất béo, chất đạm, vi-ta-min và khoáng chất
(SGK Khoa học 4 KNTHVCS)
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
2 tháng 5
Giải:
Gọi số tiền mà mẹ đưa An đóng tiền điện, tiền mước, tiền internet lần lượt là: \(x;y;z\) (đồng); \(x;y;z\) > 0
Theo bài ra ta có:
\(\dfrac{x}{7}=\dfrac{y}{5}=\dfrac{z}{2}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{x}{7}\) = \(\dfrac{y}{5}\) = \(\dfrac{z}{2}\) = \(\dfrac{x+y+z}{7+5+2}\) = \(\dfrac{5600000}{14}\) = 400 000
\(x\) = 400 000 x 7 = 2 800 000
y = 400 000 x 5 = 2 000 000
z = 400 000 x 2 = 800 000
Vậy số tiền điện, nước, internet mà bạn An phải đóng lần lượt là:
2 800 000 đồng; 2 000 000 đồng; 800 000 đồng.
NN
1
2 tháng 5
7,2:2x57,2+2,86x2x65-25%x22,88
=3,6x57,2+28,6x0,2x65-0,25x22,88
=28,6x(2x3,6+0,2x65)-5,72
=28,6x20,2-5,72
=5,72x(5x20,2-1)
=5,72x100=572
2 tháng 5
`#3107.101107`
`x^3 - 4 = 0`
`\Rightarrow x^3 = 4`
`\Rightarrow x =`\(\sqrt[3]{4}\)
Vậy, \(x=\sqrt[3]{4}.\)
2 tháng 5
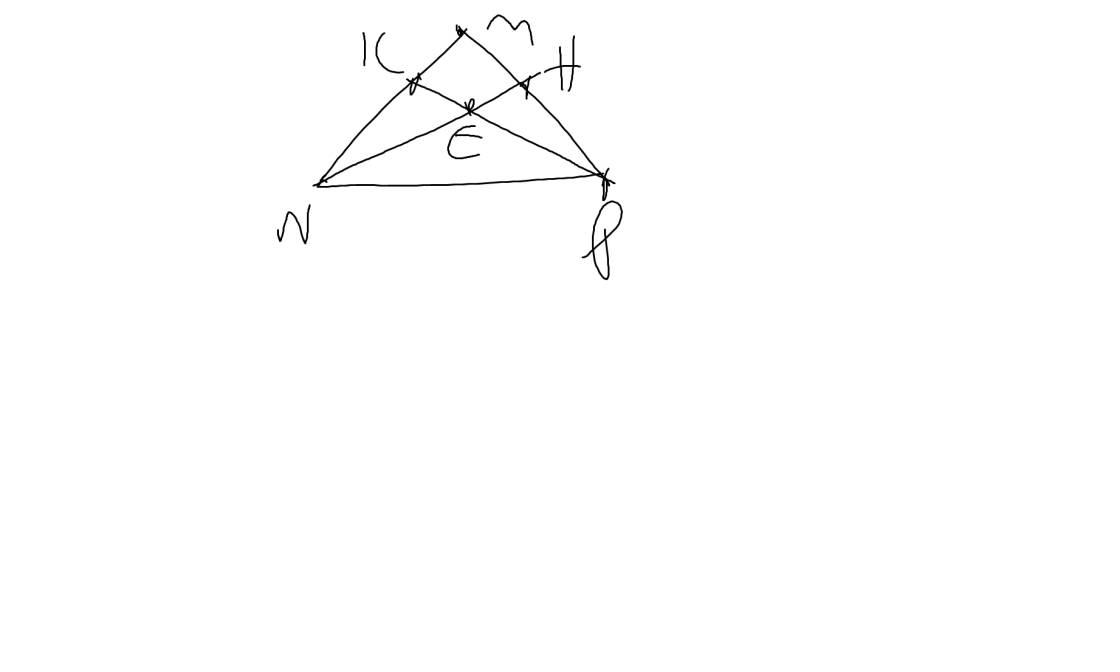
a: Xét ΔKNP vuông tại K và ΔHPN vuông tại H có
NP chung
\(\widehat{KNP}=\widehat{HPN}\)
Do đó: ΔKNP=ΔHPN
b: Xét ΔMNP có
NH,PK là các đường cao
NH cắt PK tại E
Do đó: E là trực tâm của ΔNMP
=>ME\(\perp\)NP
2 tháng 5
a: Xét ΔHBA vuông tại H và ΔABC vuông tại A có
\(\widehat{HBA}\) chung
Do đó: ΔHBA~ΔABC
=>\(\dfrac{AB}{BC}=\dfrac{HA}{AC}\)
=>\(AB\cdot AC=HA\cdot BC\)
b: Xét ΔAMH vuông tại M và ΔAHB vuông tại H có
\(\widehat{MAH}\) chung
Do đó: ΔAMH~ΔAHB
=>\(\dfrac{AM}{AH}=\dfrac{AH}{AB}\)
=>\(AH^2=AM\cdot AB\left(1\right)\)
Xét ΔANH vuông tại N và ΔAHC vuông tại H có
\(\widehat{NAH}\) chung
Do đó: ΔANH~ΔAHC
=>\(\dfrac{AN}{AH}=\dfrac{AH}{AC}\)
=>\(AN\cdot AC=AH^2\left(2\right)\)
Từ (1),(2) suy ra \(AM\cdot AB=AN\cdot AC\)
=>\(\dfrac{AM}{AC}=\dfrac{AN}{AB}\)
Xét ΔAMN vuông tạiA và ΔACB vuông tại A có
\(\dfrac{AM}{AC}=\dfrac{AN}{AB}\)
Do đó: ΔAMN~ΔACB
c:
ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC=\sqrt{6^2+8^2}=10\left(cm\right)\)
\(AH\cdot BC=AB\cdot AC\)
=>\(AH\cdot10=6\cdot8=48\)
=>AH=48/10=4,8(cm)
ΔABC vuông tại A
=>\(S_{ABC}=\dfrac{1}{2}\cdot AB\cdot AC=\dfrac{1}{2}\cdot6\cdot8=24\left(cm^2\right)\)
Xét tứ giác AMHN có \(\widehat{AMH}=\widehat{ANH}=\widehat{MAN}=90^0\)
nên AMHN là hình chữ nhật
=>MN=AH
mà AH=4,8cm
nên MN=4,8(cm)
ΔAMN~ΔACB
=>\(\dfrac{S_{AMN}}{S_{ACB}}=\left(\dfrac{MN}{CB}\right)^2=\left(\dfrac{4.8}{10}\right)^2\)
=>\(S_{AMN}=\left(\dfrac{4.8}{10}\right)^2\cdot24=5,5296\left(cm^2\right)\)
\(S_{AMN}+S_{BMNC}=S_{ABC}\)
=>\(S_{BMNC}=24-5,5296=18,4704\left(cm^2\right)\)