a. Xét Δ ABE và Δ KBE có:

^B₁=^B₂(BD là tia p/g)

^BEA=^KEB=90^o

AE chung

=> ΔABE=ΔKBE(g.c.g)

=>AB=KB

=>ΔABK cân tại B

(xin lỗi mình ko biết phần b,c,d) ;-;

cho bạn cái hình nè :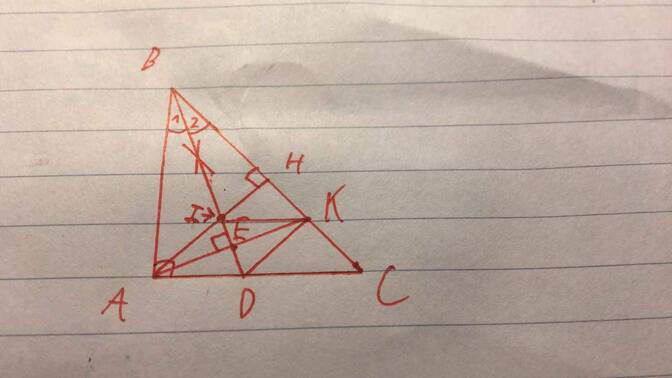

a/ Ta có

\(ME\perp AC\left(gt\right)\)

\(BH\perp AC\left(gt\right)\)

=> ME//BH (cùng vioong góc với AC)

b/

Xét tg vuông EMH và tg vuông FHM có

Ta có ME//BH (cmt) \(\Rightarrow\widehat{EMH}=\widehat{FHM}\) (góc so le trong)

MH chung

=> tg EMH = tg FHM (Hai tg vuông có cạnh huyền và góc nhọn tương ứng bằng nhau) => ME=HF

c/ Dựng đường cao CN (N thuộc AB) ta có

\(MD\perp AB\left(gt\right)\)

\(CN\perp AB\)

=> MD//CN (cùng vuông góc với AB)

\(\Rightarrow\dfrac{MD}{CN}=\dfrac{BM}{BC}\) (1)

Ta có ME//BH (cmt) \(\Rightarrow\dfrac{ME}{BH}=\dfrac{CM}{BC}\) (2)

Xét tg vuông BCN và tg vuông CBH có

BC chung

\(\widehat{ACB}=\widehat{ABC}\) (góc ở đáy tg cân)

=> tg BCN = tg CBH (Hai tg vuông có cạnh huyền và góc nhọn tương ứng bằng nhau)

=> BH=CN

Cộng 2 vế của (1) và (2)

\(\Rightarrow\dfrac{MD}{CN}+\dfrac{ME}{BH}=\dfrac{BM}{BC}+\dfrac{CM}{BC}=\dfrac{BC}{BC}=1\)

Do CN=BH (cmt)

\(\Rightarrow\dfrac{MD}{BH}+\dfrac{ME}{BH}=\dfrac{MD+ME}{BH}=1\Rightarrow MD+ME=BH\) Không đổi

d/

a) áp dụng định lí Pytago vào tam giác ABC

AB^2+AC^2=BC^2

9^2+12^2=15^2

225=15^2

Vậy tam giác ABC là tam giác vuông(đpcm)

b)Xét tam giác MHC và tam giác MKB có:

MK=MH(gt)

BM=MC(AM trung tuyến)

BMK=CMH( đđ)

Vậy tam giác MHC = tam giác MKB (đpcm)

c) I là trung điêm AB

--> CI là trung tuyến

Mà AM cũng là trung tuyến

--> G là trọng tâm

CI đi qua trọng tâm

Vậy 3 điểm I,G,C thẳng hàng(đpcm)

a) A= 12-7xy-4y^2

    B=-4+7xy+5y^2

A-B= 16-14xy-9y^2

b) Q(x)= xy+12-5xyz-713+12-2xyz

           = xy+(12+12-713)+(-5xyz-2xyz)

           = xy-689-7xyz

Chúc bạn học tốt !

\(\text{∆}'=3^2-2.2020\)

\(=-4031< 0\)

⇒ phương trình vô nghiệm

Vì 2x^2-6x > 0 với mọi x

=> 2x^2-6x+2020 > 0+2020 với mọi x

=> 2x^2-6x+2020 > 2020 với mọi x

=> A(x) > 0 ( khác 0 )

=> A(x) vô nghiệm

Bài 3. (Tự vẽ hình)

a) Xét \(\Delta DEI\) và \(\Delta DHI\)  có

\(\widehat{DEI}=\widehat{DHI}=90^0\);

\(DI\) chung

\(\widehat{EDI}=\widehat{HDI}\) (tính chất phân giác)

\(\Rightarrow\Delta DEI=\Delta DHI\) (ch - gn) 

b) Do \(IE=IH\) (hai cạnh tương ứng)

Mà \(IH< IF\) (do tam giác \(IHF\) vuông)

\(\Rightarrow IE< IF\)

c) Xét \(\Delta EIK\)  và \(\Delta HIF\) có:

\(IH=IE\)

\(\widehat{EIK}=\widehat{HIF}\) (hai góc đối đỉnh)

\(IK=IF\) (giả thiết)

\(\Rightarrow\Delta EIK=\Delta HIF\) (c.g.c) \(\Rightarrow EK=HF\) mà \(DE=DH\) (hai cạnh tương ứng)

\(\Rightarrow EK+DE=HF+HD\Rightarrow DK=DF\)

Xét \(\Delta DIK\) và \(\Delta DIF\) có:

\(DI\) chung

\(\widehat{KDI}=\widehat{FDI}\)

\(DK=DF\)

\(\Rightarrow\Delta DIK=\Delta DIF\) (c.g.c)

d) Do \(\Delta EIK=\Delta HIF\) nên \(\Rightarrow\widehat{IEK}=\widehat{IHF}=90^0\Rightarrow\widehat{DEK}=90^0+90^0=180^0\)

\(\Rightarrow D,E,K\) thẳng hàng