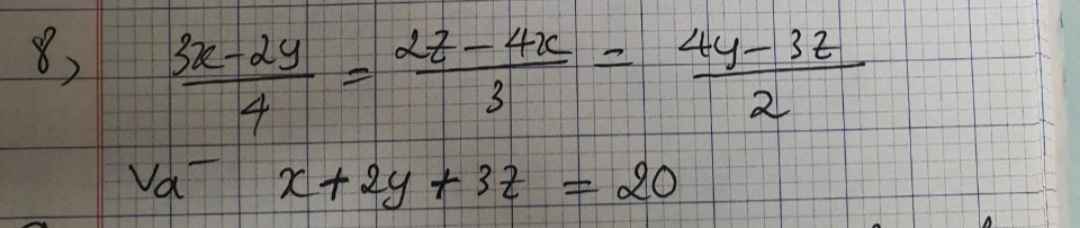\(\dfrac{3}{4\cdot7}+\dfrac{3}{7\cdot10}+\dfrac{3}{10\cdot13}+...+\dfrac{3}{87\cdot90}\)

\(=\dfrac{1}{4}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{10}+...+\dfrac{1}{87}-\dfrac{1}{90}\)

\(=\dfrac{1}{4}+\left(\dfrac{1}{7}-\dfrac{1}{7}\right)+\left(\dfrac{1}{10}-\dfrac{1}{10}\right)+...+\left(\dfrac{1}{87}-\dfrac{1}{87}\right)-\dfrac{1}{90}\)

\(=\dfrac{1}{4}-\dfrac{1}{90}\)

\(=\dfrac{45}{180}-\dfrac{2}{180}\)

\(=\dfrac{43}{180}\)

Em xem lại phân số cuối nhé, em viết sai rồi

Lời giải:
Áp dụng TCDTSBN:

$\frac{3x-2y}{4}=\frac{2z-4x}{3}=\frac{4y-3z}{2}$

$=\frac{4(3x-2y)}{16}=\frac{3(2z-4x)}{9}=\frac{2(4y-3z)}{4}$

$=\frac{4(3x-2y)+3(2z-4x)+2(4y-3z)}{16+9+4}=\frac{0}{29}=0$

$\Rightarrow 3x-2y=2z-4x=4y-3z=0$

$\Rightarrow 3x=2y; 2z=4x$

$\Rightarrow \frac{x}{2}=\frac{y}{3}; \frac{x}{2}=\frac{z}{4}$

$\Rightarrow \frac{x}{2}=\frac{y}{3}=\frac{z}{4}$

Đặt $\frac{x}{2}=\frac{y}{3}=\frac{z}{4}=t$

$\Rightarrow x=2t; y=3t; z=4t$. Khi đó:

$x+2y+3z=20$

$\Rightarrow 2t+2.3t+3.4t=20$

$\Rightarrow 2t+6t+12t=20$
$\Rightarrow 20t=20\Rightarrow t=1$

Do đó:

$x=2t=2; y=3t=3; z=4t=4$

quy đồng nhé

2,153 <  2,741

2 số thập phân thì quy đồng kiểu gì vậy?

Ta có :

\(12=2^2.3\)

\(15=3.5\)

\(=>BCNN\left(12;15\right)=3.5.2^2=3.5.4=60\)

\(=>60:12=5;60:15=4\)

\(\dfrac{5}{12}=\dfrac{5.5}{12.5}=\dfrac{25}{60}\)

\(\dfrac{8}{15}=\dfrac{8.4}{15.4}=\dfrac{32}{60}\)

Vì \(25< 32\) nên

\(=>\dfrac{25}{60}< \dfrac{32}{60}\)

\(=>\dfrac{5}{12}< \dfrac{8}{15}\)

Vậy \(\dfrac{5}{12}< \dfrac{8}{15}\)

Nếu có gì sai sót thì nhớ bảo mình , mình cảm ơn!

Tử số chung: 40

Ta có:    \(\dfrac{5}{12}\)= \(\dfrac{5.8}{12.8}\)= \(\dfrac{40}{96}\);           \(\dfrac{8}{15}\)= \(\dfrac{8.5}{15.5}\)= \(\dfrac{40}{75}\)

Vì  \(\dfrac{40}{96}\) < \(\dfrac{40}{75}\) nên \(\dfrac{5}{12}\) < \(\dfrac{8}{15}\)

Gọi số xe của đội thứ nhất, thứ hai, thứ ba lần lượt là x,y,z (xe)

Điều kiện: \(x,y,z\inℕ^∗\)

Ta có:

+) Vì đội thứ nhất nhiều hơn đội thứ ba là 10 xe nên:

\(x-z=10\)

+) Vì cùng một lượng hàng hóa thì số xe chở tỉ lệ nghịch với thời gian chở nên:

\(2x=2,5y=3z\Rightarrow\dfrac{2x}{30}=\dfrac{2,5y}{30}=\dfrac{3z}{30}\Rightarrow\dfrac{x}{15}=\dfrac{y}{12}=\dfrac{z}{10}\)

Áp dụng tính chất dãy tỉ số bằng nhau kết hợp \(x-z=10\) được:

\(\dfrac{x}{15}=\dfrac{y}{12}=\dfrac{z}{10}=\dfrac{x-z}{15-10}=\dfrac{10}{5}=2\)

Do đó:

\(\left\{{}\begin{matrix}x=15\cdot2=30\\y=12\cdot2=24\\z=10\cdot2=20\end{matrix}\right.\) (thỏa mãn điều kiện)

Vậy...

Gọi số thợ của nhóm thứ nhất, nhóm thứ hai, nhóm thứ ba lần lượt là a(người),b(người),c(người)

(Điều kiện: \(a,b,c\in Z^+\))

Nhóm thứ nhất xây xong trong 40 ngày, nhóm thứ hai xây xong trong 60 ngày, nhóm thứ ba xây xong trong 50 ngày nên ta có: 40a=60b=50c

=>4a=6b=5c

=>\(\dfrac{4a}{60}=\dfrac{6b}{60}=\dfrac{5c}{60}\)

=>\(\dfrac{a}{15}=\dfrac{b}{10}=\dfrac{c}{12}\)

Nhóm thứ ba có ít hơn nhóm thứ nhất là 3 người nên a-c=3

Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:

\(\dfrac{a}{15}=\dfrac{b}{10}=\dfrac{c}{12}=\dfrac{a-c}{15-12}=\dfrac{3}{3}=1\)

=>\(a=15\cdot1=15;b=10\cdot1=10;c=12\cdot1=12\)

Vậy: số thợ của nhóm thứ nhất, nhóm thứ hai, nhóm thứ ba lần lượt là 15(người),10(người),12(người)

Ta có số đó góc D, E, F của tam giác DEF tỉ lệ nghịch với 2, 3, 6 nên ta có: 

\(2\widehat{D}=3\widehat{E}=6\widehat{F}\\ \Rightarrow\dfrac{2\widehat{D}}{12}=\dfrac{3\widehat{E}}{12}=\dfrac{\widehat{6F}}{12}\\ \Rightarrow\dfrac{\widehat{D}}{6}=\dfrac{\widehat{E}}{4}=\dfrac{\widehat{F}}{2}\)

Mà: \(\widehat{D}+\widehat{E}+\widehat{F}=180^o\)

Áp dụng tính chất dãy tỉ số bằng nhau ta có:

\(\dfrac{\widehat{D}}{6}=\dfrac{\widehat{E}}{4}=\dfrac{\widehat{F}}{2}=\dfrac{\widehat{D}+\widehat{E}+\widehat{F}}{6+4+2}=\dfrac{180^o}{12}=15^o\)

\(\Rightarrow\widehat{D}=6\cdot15^o=90^o;\widehat{E}=15^o\cdot4=60^o;\widehat{F}=2\cdot15^o=30^o\)

Gọi số đo 3 góc D,E,F của ΔDEF lần lượt là \(d;e;f\) (^o) 

Điều kiện: \(d;e;f>0\)

Ta có:

+) \(d+e+f=180\) (theo định lý)

+) \(d;e;f\) tỉ lệ nghịch với 2,3,6 nên:

\(2d=3e=6f\)

\(\Rightarrow\dfrac{2d}{6}=\dfrac{3e}{6}=\dfrac{6f}{6}\)

\(\Rightarrow\dfrac{d}{3}=\dfrac{e}{2}=\dfrac{f}{1}\)

Áp dụng tính chất dãy tỉ số bằng nhau kết hợp \(d+e+f=180\) được:

\(\dfrac{d}{3}=\dfrac{e}{2}=\dfrac{f}{1}=\dfrac{d+e+f}{3+2+1}=\dfrac{180}{6}=30\)

Do đó:

\(\left\{{}\begin{matrix}d=3\cdot30=90\\e=2\cdot30=60\\f=1\cdot30=30\end{matrix}\right.\) (thỏa mãn điều kiện)

Vậy số đo 3 góc D,E,F của ΔDEF lần lượt là 90^o;60^o;30^o

15-25.8:(100.2)

=15-25.8:200

=15-200:200

=15-1

=14

\(15-25\cdot8:\left(100\cdot2\right)\)

\(=15-\dfrac{200}{200}\)

=15-1

=14