Hai vận động viên chạy xung quanh một sân vận động. Hai vận động viên xuất phát tại cùng một thời điểm, cùng vị trí và chạy cùng chiều. Vận động viên thứ nhất chạy một vòng sân hết 360 giây, Vận động viên thứ hai chạy một vòng sân mất 420 giây. Hỏi sau bao nhiêu phút họ gặp lại nhau, biết tốc độ di chuyển của họ không đổi?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có \(\sqrt{2+2\cos2x}=\sqrt{2+2\left(2\cos^2x-1\right)}=\sqrt{4\cos^2x}=2\left|\cos x\right|\)
\(\Leftrightarrow f\left(x\right)+f\left(-x\right)=2\left|\cos x\right|,\forall x\inℝ\) (1)
Đặt \(g\left(x\right)=f\left(x\right)-\left|\cos x\right|\)
Khi đó (1) \(\Leftrightarrow\left[f\left(x\right)-\left|\cos x\right|\right]+\left[f\left(-x\right)-\left|\cos x\right|\right]=0\)
\(\Leftrightarrow g\left(x\right)+\left[f\left(-x\right)-\left|\cos\left(-x\right)\right|\right]=0\) (do \(\cos x\) là hàm chẵn)
\(\Leftrightarrow g\left(x\right)+g\left(-x\right)=0\)
\(\Leftrightarrow g\left(x\right)=-g\left(-x\right)\)
\(\Leftrightarrow g\left(x\right)\) là hàm lẻ
Khi đó \(f\left(x\right)=g\left(x\right)+\left|\cos x\right|\) với \(g\left(x\right)\) là hàm lẻ. Thử lại, ta thấy:
(1) \(\Leftrightarrow f\left(x\right)+f\left(-x\right)=g\left(x\right)+\left|\cos x\right|+g\left(-x\right)+\left|\cos\left(-x\right)\right|\)
\(\Leftrightarrow f\left(x\right)+f\left(-x\right)=2\left|\cos x\right|\), thỏa mãn
Vậy \(f\left(x\right)=g\left(x\right)+\left|\cos x\right|\) với \(g\left(x\right)\) là hàm lẻ bất kì có tập xác định là \(ℝ\)
\(\Rightarrow I=\int\limits^{\dfrac{3\pi}{2}}_{-\dfrac{3\pi}{2}}f\left(x\right)dx\)
\(I=\int\limits^{\dfrac{3\pi}{2}}_{-\dfrac{3\pi}{2}}\left[g\left(x\right)+\left|\cos x\right|\right]dx\)
\(I=\int\limits^{\dfrac{3\pi}{2}}_{-\dfrac{3\pi}{2}}g\left(x\right)dx+\int\limits^{\dfrac{3\pi}{2}}_{-\dfrac{3\pi}{2}}\left|\cos x\right|dx\)
\(I=\int\limits^{\dfrac{3\pi}{2}}_{-\dfrac{3\pi}{2}}\left|\cos x\right|dx\) (do \(g\left(x\right)\) là hàm lẻ)
\(I=\int\limits^{-\dfrac{\pi}{2}}_{-\dfrac{3\pi}{2}}\left(-\cos x\right)dx+\int\limits^{\dfrac{\pi}{2}}_{-\dfrac{\pi}{2}}\cos xdx+\int\limits^{\dfrac{3\pi}{2}}_{\dfrac{\pi}{2}}\left(-\cos x\right)dx\)
\(I=-\sin x|^{-\dfrac{\pi}{2}}_{-\dfrac{3\pi}{2}}+\sin x|^{\dfrac{\pi}{2}}_{-\dfrac{\pi}{2}}-\sin x|^{\dfrac{3\pi}{2}}_{\dfrac{\pi}{2}}\)
\(I=6\)

Giải:
Các số thập phân lớn hơn 24,5 và nhỏ hơn 25,2 mà chỉ có một chữ số ở phần thập phân là các số thuộc dãy số sau:
24,6; 24,7; 24,8;...; 25,1
Dãy số trên là dãy số cách đều với khoảng cách là:
24,7 - 24,6 = 0,1
Số số hạng của dãy số trên là: (25,1 - 24,6) : 0,1 + 1 = 6
Vậy có tất cả 6 số lớn hơn 24,5 và nhỏ hơn 25,2 là 6 số.
Các số thập phân lớn hơn 24,5 và nhỏ hơn 25,2 mà có 2 chữ số ở phần thập phân là:
24,51;24,52;...;25,19
Số số thập phân thỏa mãn là:
(25,19-24,51):0,01+1=69(số)

a: 12m23dm=14,3m
b: 3 tấn 123 yến=4,23 tấn
3km234m=3,234km
2kg3562g=5,562kg

ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(AC=\sqrt{4^2-2^2}=2\sqrt{3}\left(cm\right)\)
Xét ΔABC vuông tại A có \(cosB=\dfrac{BA}{BC}=\dfrac{1}{2}\)
nên \(\widehat{B}=60^0\)

a: Xét tứ giác BEDC có \(\widehat{BEC}=\widehat{BDC}=90^0\)
nên BEDC là tứ giác nội tiếp
=>B,E,D,C cùng thuộc một đường tròn
b: Xét (B;BD) có
BD là bán kính
AC\(\perp\)BD tại D
Do đó: AC là tiếp tuyến của (B;BD)

A = 2022 x 98,76 + 2023 x 1,24 - 2,48 : 2
A = 2022 x 98,76 + (2022 + 1) x 1,24 - 1,24
A = 2022 x 98,76 + 2022 x 1,24 + 1,24 - 1,24
A = 2022 x (98,76 + 1,24) + (1,24 - 1,24)
A = 2022 x 100 + 0
A = 202200

a: Xét (O) có
\(\widehat{ABC};\widehat{ADC}\) là các góc nội tiếp chắn cung AC
nên \(\widehat{ABC}=\widehat{ADC}\)
Xét (O) có
ΔACD nội tiếp
AD là đường kính
Do đó: ΔACD vuông tại C
Xét ΔAHB vuông tại H và ΔACD vuông tại C có
\(\widehat{ABH}=\widehat{ADC}\)
Do đó: ΔAHB~ΔACD
b: ΔAHB~ΔACD
=>\(\dfrac{AH}{AC}=\dfrac{AB}{AD}\)
=>\(AD=\dfrac{AB\cdot AC}{AH}=\dfrac{8\cdot15}{5}=8\cdot3=24\left(cm\right)\)
Bán kính của (O) là 24:2=12(cm)

a: Xét (O) có \(\widehat{BAC}\) là góc nội tiếp chắn cung BC
nên \(\widehat{BAC}=\dfrac{1}{2}\cdot\widehat{BOC}\)
Xét ΔOBC có OB=OC
nên ΔOBC cân tại O
=>\(\widehat{OBC}=\dfrac{180^0-\widehat{BOC}}{2}=90^0-\widehat{BAC}\)
b: H là trực tâm của ΔABC
=>AH\(\perp\)BC
=>\(\widehat{BAH}=90^0-\widehat{ABC}\left(1\right)\)
Xét ΔOAC có OA=OC
nên ΔOAC cân tại O
=>\(\widehat{OAC}=\dfrac{180^0-\widehat{AOC}}{2}=90^0-\dfrac{1}{2}\cdot\widehat{AOC}=90^0-\widehat{ABC}\left(2\right)\)
Từ (1),(2) suy ra \(\widehat{BAH}=\widehat{OAC}\)



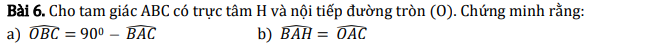
\(360=2^3\cdot3^2\cdot5;420=2^2\cdot3\cdot5\cdot7\)
=>\(BCNN\left(360;420\right)=2^3\cdot3^2\cdot5\cdot7=2520\)
Vì vận động viên thứ nhất chạy một vòng hết 360 giây, vận động viên thứ hai chạy một vòng hết 420 giây nên sau ít nhất là BCNN(360;420)=2520 giây thì hai VĐV này mới lại gặp nhau
=>Sau ít nhất là 2520 giây=42 phút thì hai người mới gặp lại nhau
sau 42 phút