Cho đường tròn tâm o bán kính r và một dây cung bc không đi qua tâm o lấy điểm a trên cung lớn bc sao cho abc nhọn . Các đường cao AD , BE, CF đồng quy tại H. Các đường thẳng BE và CF cắt đường tròn tâm o tại điểm thứ hai lần lượt là Q và P a, chứng minh :tứ giác BFEC là tứ giác nội tiếp và PQ//EF b, Gọi i là trung điểm của BC . Chứng minh :FDE=2ABE và FDE=FIE
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi vận tốc xe máy là x(km/h)
(ĐK: x>0)
Vận tốc xe ô tô là x+20(km/h)
CB=AB-AC=80km
Thời gian ô tô đi từ B đến chỗ gặp là \(\dfrac{80}{x+20}\left(giờ\right)\)
Thời gian xe máy đi từ A đến chỗ gặp là \(\dfrac{120}{x}\left(giờ\right)\)
Do đó, ta có phương trình:
\(\dfrac{80}{x+20}=\dfrac{120}{x}\)
=>\(\dfrac{2}{x+20}=\dfrac{3}{x}\)
=>3(x+20)=2x
=>3x+60=2x
=>x=-60
=>Đề sai rồi bạn

Gọi (d): y=ax+b\(\left(a\ne0\right)\) là phương trình đường thẳng cần tìm
Thay x=1 và y=3 vào (d), ta được:
\(a\cdot1+b=3\)
=>a+b=3(1)
Thay x=-4 và y=-7 vào (d), ta được:
\(a\cdot\left(-4\right)+b=-7\)
=>-4a+b=-7(2)
Từ (1),(2) ta có hệ phương trình:
\(\left\{{}\begin{matrix}a+b=3\\-4a+b=-7\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}5a=10\\a+b=3\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}a=2\left(nhận\right)\\b=3-2=1\end{matrix}\right.\)
vậy: (d): y=2x+1

Bạn nên viết đề bằng công thức toán (biểu tượng $\sum$ góc trái khung soạn thảo) để mọi người đọc hiểu đề của bạn hơn nhé.

Người ra đề cho con số tào lao quá, dẫn tới đẳng thức của BĐT này ko xảy ra. (vế trái lớn hơn vế phải tuyệt đối, thậm chí là hơn rất xa).
Ta có:
\(ab+bc+ca\ge3\sqrt[3]{a^2b^2c^2}\Rightarrow abc\le\dfrac{1}{3\sqrt{3}}\)
\(\Rightarrow8\sqrt{3}abc\le\dfrac{8}{3}\)
Đặt vế trái BĐT cần chứng minh là P:
\(P=\left[\left(a+1\right)\left(b+1\right)\left(c+1\right)\right]^2+\left[\left(a-1\right)\left(b-1\right)\left(c-1\right)\right]^2\)
\(=\left(abc+a+b+c+ab+bc+ca+1\right)^2+\left(abc+a+b+c-ab-bc-ca-1\right)^2\)
\(=\left(abc+a+b+c+2\right)^2+\left(abc+a+b+c-2\right)^2\)
\(=\left(abc+a+b+c\right)^2+4>\dfrac{8}{3}\ge8\sqrt{3}abc\) (đpcm)

a: Xét ΔAHB vuông tại H có HK là đường cao
nên \(AK\cdot AB=AH^2\left(1\right)\)
Xét ΔAHC vuông tại H có HL là đường cao
nên \(AL\cdot AC=AH^2\left(2\right)\)
Từ (1),(2) suy ra \(AK\cdot AB=AL\cdot AC\)
=>\(\dfrac{AK}{AC}=\dfrac{AL}{AB}\)
Xét ΔAKL và ΔACB có
\(\dfrac{AK}{AC}=\dfrac{AL}{AB}\)
\(\widehat{BAC}\) chung
Do đó: ΔAKL~ΔACB
=>\(\widehat{AKL}=\widehat{ACB}\)
=>\(\widehat{BKL}+\widehat{BCL}=180^0\)
=>BKLC là tứ giác nội tiếp

b.
\(\left\{{}\begin{matrix}BD\perp AC\\CE\perp AB\end{matrix}\right.\) đồng thời H là giao điểm BD, CE
\(\Rightarrow H\) là trực tâm tam giác ABC
\(\Rightarrow AF\) là đường cao thứ 3 \(\Rightarrow\widehat{AFC}=90^0\)
\(\Rightarrow\widehat{FAC}+\widehat{FCA}=180^0-\widehat{AFC}=90^0\) (1)
ADHE nội tiếp đường tròn đường kính AH, mà M là trung điểm AH
\(\Rightarrow M\) là tâm đường tròn đường kính AH
\(\Rightarrow MA=MD\Rightarrow\Delta MAD\) cân tại M
\(\Rightarrow\widehat{FAC}=\widehat{MDA}\) (2)
D, C cùng thuộc (O) \(\Rightarrow OD=OC\Rightarrow\Delta OCD\) cân tại O
\(\Rightarrow\widehat{FCA}=\widehat{ODC}\) (3)
(1);(2);(3) \(\Rightarrow\widehat{MDA}+\widehat{ODC}=90^0\)
\(\Rightarrow\widehat{MDO}=180^0-\left(\widehat{MDA}+\widehat{ODC}\right)=90^0\)
\(\Rightarrow MD\perp OD\)
\(\Rightarrow MD\) là tiếp tuyến tại D của (O)

\(P=2\left(a+b\right)-ab-7+7=2\left(a+b\right)-ab-\left(a^2+b^2+ab\right)+7\)
\(=2\left(a+b\right)-\left(a^2+2ab+b^2\right)+7\)
\(=2\left(a+b\right)-\left(a+b\right)^2+7\)
\(=8-\left(a+b-1\right)^2\le8\)
\(P_{max}=8\) khi \(\left\{{}\begin{matrix}a+b=1\\a^2+b^2+ab=7\end{matrix}\right.\) \(\Rightarrow\left(a;b\right)=\left(-2;3\right);\left(3;-2\right)\)



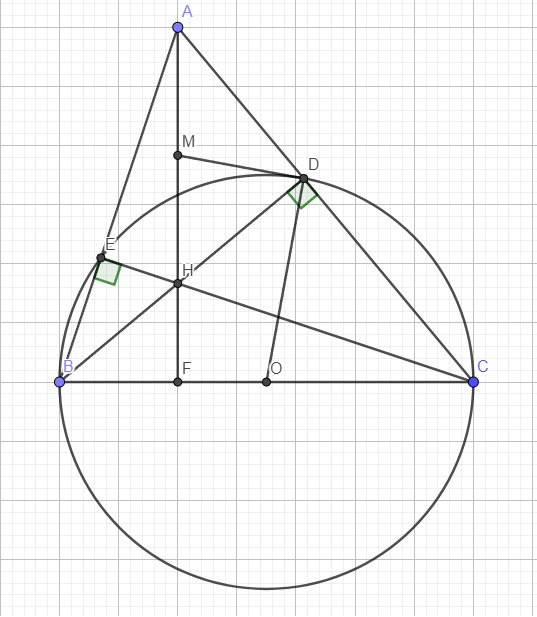
a: Xét tứ giác BFEC có \(\widehat{BFC}=\widehat{BEC}=90^0\)
nên BFEC là tứ giác nội tiếp đường tròn đường kính BC
Xét (O) có
\(\widehat{CPQ}\) là góc nội tiếp chắn cung CQ
\(\widehat{CBQ}\) là góc nội tiếp chắn cung CQ
Do đó: \(\widehat{CPQ}=\widehat{CBQ}\)
=>\(\widehat{HPQ}=\widehat{HFE}\)
=>PQ//FE
b: Vì BFEC là tứ giác nội tiếp đường tròn đường kính BC
nên BFEC nội tiếp (I)
=>IF=IE=IB=IC
Xét ΔICE có \(\widehat{EIB}\) là góc ngoài tại đỉnh I
nên \(\widehat{EIB}=\widehat{IEC}+\widehat{ICE}=2\cdot\widehat{ACB}\)
Xét tứ giác AFDC có \(\widehat{AFC}=\widehat{ADC}=90^0\)
nên AFDC là tứ giác nội tiếp
=>\(\widehat{BFD}=\widehat{BCA}\left(=180^0-\widehat{AFD}\right)\)
Vì BFEC là tứ giác nội tiếp
nên \(\widehat{AFE}=\widehat{ACB}\left(=180^0-\widehat{EFB}\right)\)
\(\widehat{AFE}+\widehat{EFD}+\widehat{BFD}=180^0\)
=>\(\widehat{EFD}+\widehat{ACB}+\widehat{ACB}=180^0\)
=>\(\widehat{EFD}+2\cdot\widehat{ACB}=180^0\)
=>\(\widehat{EFD}+\widehat{EID}=180^0\)
=>EFDI là tứ giác nội tiếp
=>\(\widehat{FDE}=\widehat{FIE}\)
Xét (I) có
\(\widehat{FCE}\) là góc nội tiếp chắn cung FE
nên \(\widehat{FCE}=\dfrac{\widehat{FIE}}{2}\)
=>\(\widehat{FIE}=2\cdot\widehat{FCE}=2\cdot\widehat{ACF}=2\cdot\widehat{ABE}\)