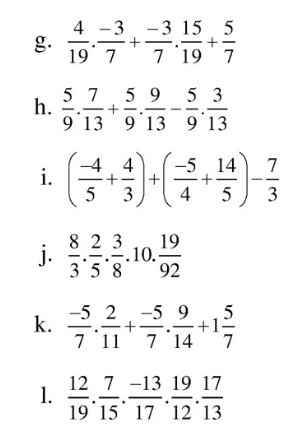
Mn ơi,giúp mk mấy câu này đc ko?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Biểu thức mẫu là $\sqrt{4}-x^2$ hay $\sqrt{4-x^2}$ vậy bạn?

Số số tự nhiên có thể lập được là:
5x4x3x2x1=120(số)

a: Vì \(AD=\dfrac{1}{3}AC\)
nên \(S_{ABD}=\dfrac{1}{3}\times S_{ABC}\)
=>\(\dfrac{S_{ABD}}{S_{ABC}}=\dfrac{1}{3}\)
b: Vì \(AE=\dfrac{2}{3}AB\)
nên \(S_{AED}=\dfrac{2}{3}\times S_{ABD}=\dfrac{2}{9}\times S_{ABC}\)
=>\(S_{ABC}=4,5\times S_{AED}=4,5\times8=36\left(cm^2\right)\)

CN=3NA
=>\(\dfrac{NA}{NC}=\dfrac{1}{3}\)
E,N,M thẳng hàng
=>\(\dfrac{EA}{EB}\times\dfrac{NC}{NA}\times\dfrac{MB}{MC}=1\)
=>\(\dfrac{EA}{EB}\times3=1\)
=>\(\dfrac{EA}{EB}=\dfrac{1}{3}\)
=>\(\dfrac{EA}{AB}=\dfrac{1}{2}\)
=>AB=2EA
=>\(S_{NAB}=2\times S_{NEA}=54\left(cm^2\right)\)
Vì NC=3NA
nên \(\dfrac{AN}{AC}=\dfrac{1}{4}\)
=>AC=4AN
=>\(S_{ABC}=4\times S_{ABN}=216\left(cm^2\right)\)

Câu 1 Giải:
Độ dài của đường chéo còn lại của hình thoi là:
40 x 2 : 8 = 10 (dm)
Chọn B,10 dm
Câu 2:
Tím số tự nhiên \(x\) biết: 5\(x\) + 3\(x\) = 88
Giải:
5\(x\) + 3\(x\) = 88
(5 + 3)\(\times\) \(x\)= 88
8\(x\) = 88
\(x\) = 88 : 8
\(x=11\)
Chọn A,11

Giải:
Từ 1 đến 112 có các số lẻ là các số lần lượt thuộc dãy số sau:
1; 3; 5; 7; 9; 11;...; 111
Đây là dãy số cách đều với khoảng cách là:
3 - 1 = 2
Dãy số trên có số các số hạng là:
(111 - 1) : 2 + 1 = 56 (số hạng)
Vậy từ 1 đến 112 có 56 số lẻ
Đáp số: 56 số lẻ

Olm chào em, em sử dụng phần mềm hình học em nhé.
`#3107.101107`
`g)`
\(\dfrac{4}{19}\cdot\dfrac{-3}{7}+\dfrac{-3}{7}\cdot\dfrac{15}{19}+\dfrac{5}{7}\)
\(=\dfrac{-3}{7}\left(\dfrac{4}{19}+\dfrac{15}{19}\right)+\dfrac{5}{7}\)
\(=\dfrac{-3}{7}\cdot1+\dfrac{5}{7}\)
\(=-\dfrac{3}{7}+\dfrac{5}{7}=\dfrac{2}{7}\)
`h)`
\(\dfrac{5}{9}\cdot\dfrac{7}{13}+\dfrac{5}{9}\cdot\dfrac{9}{13}-\dfrac{5}{9}\cdot\dfrac{3}{13}\)
\(=\dfrac{5}{9}\cdot\left(\dfrac{7}{13}+\dfrac{9}{13}-\dfrac{3}{13}\right)\)
\(=\dfrac{5}{9}\cdot\left(\dfrac{7+9-3}{13}\right)\)
\(=\dfrac{5}{9}\cdot1=\dfrac{5}{9}\)
`i)`
\(\left(\dfrac{-4}{5}+\dfrac{4}{3}\right)+\left(\dfrac{-5}{4}+\dfrac{14}{5}\right)-\dfrac{7}{3}\)
\(=\dfrac{-4}{5}+\dfrac{4}{3}+\dfrac{-5}{4}+\dfrac{14}{5}-\dfrac{7}{3}\)
\(=\left(-\dfrac{4}{5}+\dfrac{14}{5}\right)+\left(\dfrac{4}{3}-\dfrac{7}{3}\right)-\dfrac{5}{4}\)
\(=\dfrac{10}{5}+\dfrac{-3}{3}-\dfrac{5}{4}\)
\(=2-1-\dfrac{5}{4}\)
\(=1-\dfrac{5}{4}\)
\(=-\dfrac{1}{4}\)
`j)`
\(\dfrac{8}{3}\cdot\dfrac{2}{5}\cdot\dfrac{3}{8}\cdot10\cdot\dfrac{19}{92}\)
\(=\left(\dfrac{8}{3}\cdot\dfrac{3}{8}\right)\cdot\left(\dfrac{2}{5}\cdot10\right)\cdot\dfrac{19}{92}\)
\(=1\cdot\dfrac{20}{5}\cdot\dfrac{19}{92}\)
\(=4\cdot\dfrac{19}{92}=\dfrac{19}{23}\)
`k)`
\(\dfrac{-5}{7}\cdot\dfrac{2}{11}+\dfrac{-5}{7}\cdot\dfrac{9}{14}+1\dfrac{5}{7}\)
\(=-\dfrac{5}{7}\cdot\dfrac{2}{11}-\dfrac{5}{7}\cdot\dfrac{9}{14}+1+\dfrac{5}{7}\)
\(=\dfrac{5}{7}\cdot\left(-\dfrac{2}{11}-\dfrac{9}{14}+1\right)+1\)
\(=\dfrac{5}{7}\cdot\dfrac{27}{154}+1\)
\(=\dfrac{135}{1078}+1=\dfrac{1213}{1078}\)
`l)`
\(\dfrac{12}{19}\cdot\dfrac{7}{15}\cdot\dfrac{-13}{17}\cdot\dfrac{19}{12}\cdot\dfrac{17}{13}\)
\(=\left(\dfrac{12}{19}\cdot\dfrac{19}{12}\right)\cdot\left(-\dfrac{13}{17}\cdot\dfrac{17}{13}\right)\cdot\dfrac{7}{15}\)
\(=1\cdot\left(-1\right)\cdot\dfrac{7}{15}=-\dfrac{7}{15}\)
sos