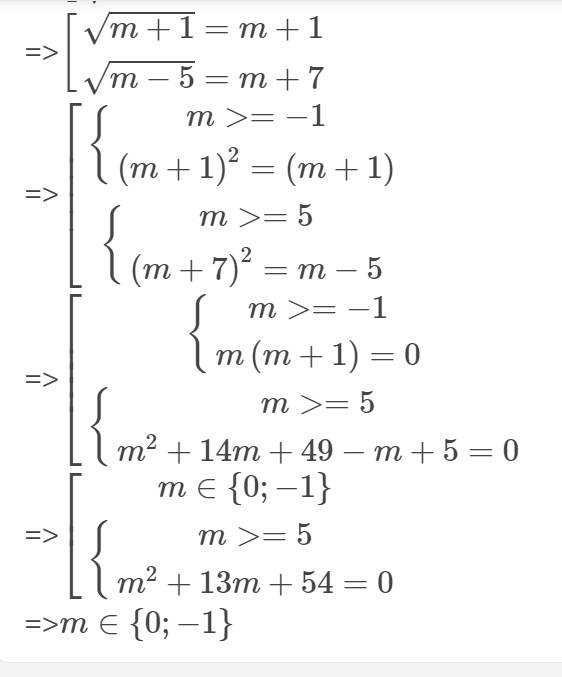
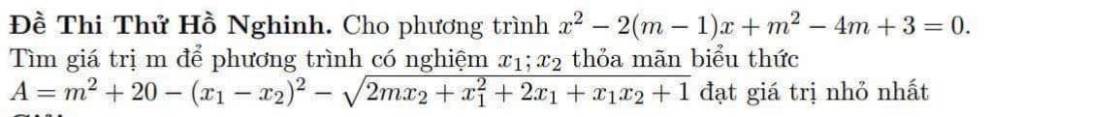
a: Phương trình hoành độ giao điểm là:

\(x^2=2\left(m-2\right)x-m^2+4m+5\)

=>\(x^2-\left(2m-4\right)x+m^2-4m-5=0\)(1)

\(\Delta=\left[-\left(2m-4\right)\right]^2-4\cdot1\cdot\left(m^2-4m-5\right)\)

\(=4m^2-16m+16-4m^2+16m+20=36\)>0

=>(P) luôn cắt (d) tại hai điểm phân biệt

b: Vì \(\Delta=36\)

nên phương trình (1) luôn có 2 nghiệm phân biệt là:

\(\left[{}\begin{matrix}x=\dfrac{2m-4+\sqrt{36}}{2}=\dfrac{2m-4+6}{2}=\dfrac{2m+2}{2}=m+1\\x=\dfrac{2m-4-6}{2}=\dfrac{2m-10}{2}=m-5\end{matrix}\right.\)

\(\sqrt{x_1}=x_2+6\)

=>\(\left[{}\begin{matrix}\sqrt{m+1}=m-5+6\\\sqrt{m-5}=m+1+6\end{matrix}\right.\)

=>\(\left[{}\begin{matrix}\sqrt{m+1}=m+1\\\sqrt{m-5}=m+7\end{matrix}\right.\)

=>\(\left[{}\begin{matrix}\left\{{}\begin{matrix}m>=-1\\\left(m+1\right)^2=\left(m+1\right)\end{matrix}\right.\\\left\{{}\begin{matrix}m>=5\\\left(m+7\right)^2=m-5\end{matrix}\right.\end{matrix}\right.\)

=>\(\left[{}\begin{matrix}\left\{{}\begin{matrix}m>=-1\\m\left(m+1\right)=0\end{matrix}\right.\\\left\{{}\begin{matrix}m>=5\\m^2+14m+49-m+5=0\end{matrix}\right.\end{matrix}\right.\)

=>\(\left[{}\begin{matrix}m\in\left\{0;-1\right\}\\\left\{{}\begin{matrix}m>=5\\m^2+13m+54=0\end{matrix}\right.\end{matrix}\right.\)

=>\(m\in\left\{0;-1\right\}\)

\(P=\dfrac{2x+\sqrt{x}}{\sqrt{x}}-\dfrac{x\sqrt{x}+1}{x-\sqrt{x}+1}+1\)

\(=\dfrac{\sqrt{x}\left(2\sqrt{x}+1\right)}{\sqrt{x}}-\dfrac{\left(\sqrt{x}+1\right)\left(x-\sqrt{x}+1\right)}{x-\sqrt{x}+1}+1\)

\(=2\sqrt{x}+1-\sqrt{x}-1+1\)

\(=\sqrt{x}+3\)

\(P=\dfrac{2x+\sqrt{x}}{\sqrt{x}}-\dfrac{x\sqrt{x}+1}{x-\sqrt{x}+1}+1\)

\(P=\dfrac{\sqrt{x}\left(2\sqrt{x}+1\right)}{\sqrt{x}}-\dfrac{\left(\sqrt{x}+1\right)\left(x-\sqrt{x}+1\right)}{x-\sqrt{x}+1}+1\)

\(P=2\sqrt{x}+1-\sqrt{x}-1+1\)

\(P=\sqrt{x}+1\)

giải GIÚP MIK VS Ạ NHANH LÊN Ạ(  hiếm khi đẳng câu hỏi chẳng có ai huóng dẫn, thật sự ******** quá vô dụng)

Lời giải:
Áp dụng BĐT Cô-si:

$\frac{x}{4}+\frac{1}{x}\geq 2\sqrt{\frac{x}{4}.\frac{1}{x}}=1$
$\frac{3}{4}x\geq \frac{3}{4}.2=\frac{3}{2}$ do $x\geq 2$

Cộng theo vế 2 BĐT trên thu được:

$A\geq 1+\frac{3}{2}=\frac{5}{2}$
Vậy GTNN của $A$ là $\frac{5}{2}$. Giá trị này đạt được tại $x=2$

Lời giải:

Áp dụng BĐT Cauchy Schwarz:

$A=\frac{a^2}{a+b}+\frac{b^2}{c+a}+\frac{c^2}{b+c}\geq \frac{(a+b+c)^2}{a+b+c+a+b+c}=\frac{(a+b+c)^2}{2(a+b+c)}=\frac{a+b+c}{2}\geq \frac{6}{2}=3$
Vậy $A_{\min}=3$. Giá trị này đạt tại $a=b=c=2$

1: Xét (O) có

ΔADB nội tiếp

AB là đường kính

Do đó: ΔADB vuông tại D

Xét tứ giác ADHM có \(\widehat{ADM}=\widehat{AHM}=90^0\)

nên ADHM là tứ giác nội tiếp

2: Xét (O) có

\(\widehat{CAD}\) là góc tạo bởi tiếp tuyến AC và dây cung AD

\(\widehat{AED}\) là góc nội tiếp chắn cung AD

Do đó: \(\widehat{CAD}=\widehat{AED}\)

Xét ΔCAD và ΔCEA có

\(\widehat{CAD}=\widehat{CEA}\)

\(\widehat{ACD}\) chung

Do đó: ΔCAD~ΔCEA

=>\(\dfrac{CA}{CE}=\dfrac{CD}{CA}\)

=>\(CA^2=CE\cdot CD\left(1\right)\)

Xét ΔCAO vuông tại A có AH là đường cao

nên \(CH\cdot CO=CA^2\left(2\right)\)

Từ (1),(2) suy ra \(CE\cdot CD=CH\cdot CO\)

Câu 5:

Gọi giá niêm yết của tivi là x(triệu đồng)

(Điều kiện: x>0)

Giá của tivi nếu mua ở cửa hàng A là:

\(x\cdot\left(1-15\%\right)-0,8=0,85x-0,8\)(triệu đồng)

Giá của tivi nếu mua ở cửa hàng B là:

\(x\left(1-20\%\right)=0,8x\left(triệuđồng\right)\)

Theo đề, ta có phương trình:

0,8x-(0,85x-0,8)=0,2

=>0,8-0,05x=0,2

=>0,05x=0,6

=>x=0,6:0,05=12(nhận)

vậy: Giá niêm yết của tivi là 12 triệu đồng

Câu 2:

Theo Vi-et, ta có:

\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=\dfrac{-\left(-1\right)}{2}=\dfrac{1}{2}\\x_1x_2=\dfrac{c}{a}=-\dfrac{7}{2}\end{matrix}\right.\)

\(Q=\left(x_1-x_2\right)^2-5x_1-5x_2\)

\(=\left(x_1+x_2\right)^2-4x_1x_2-5\left(x_1+x_2\right)\)

\(=\left(\dfrac{1}{2}\right)^2-4\cdot\dfrac{-7}{2}-5\cdot\dfrac{1}{2}\)

\(=\dfrac{1}{4}+14-\dfrac{5}{2}=\dfrac{47}{4}\)