 Cần gấp ạ!!!
Cần gấp ạ!!!
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có: `x+y=a+b`
`\Leftrightarrow (x+y)^2=(a+b)^2`
`\Leftrightarrow x^2+2xy+y^2=a^+2ab+b^2`
`\Leftrightarrow 2xy=2ab` (vì `x^2+y^2=a^2+b^2`)
`\Leftrightarrow xy=ab`
Khi đó: `x^3+y^3=(x+y)(x^2-xy+y^2)`
`=(a+b)(a^2-ab+b^2)=a^3+b^3` (đpcm)


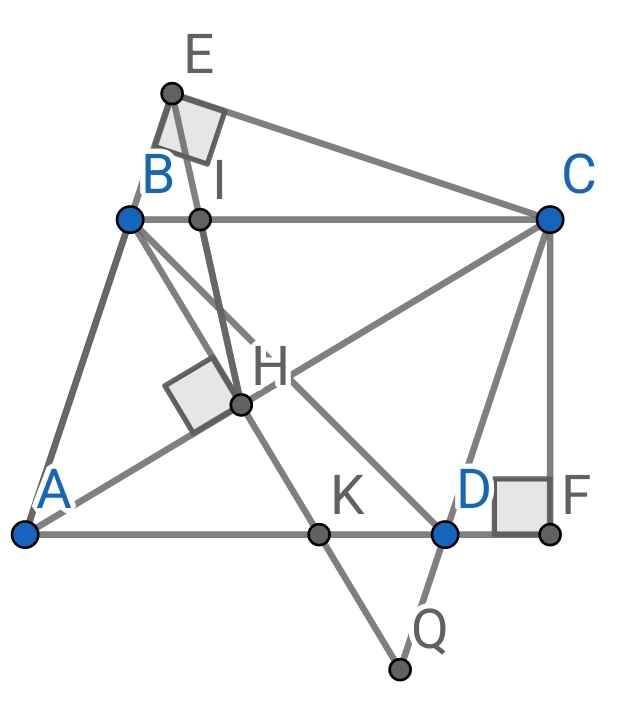
1) Xét hai tam giác vuông: ∆ABH và ∆ACE có:
∠A chung
∆ABH ∽ ∆ACE (g-g)
 ⇒ AB.AE = AH.AC
⇒ AB.AE = AH.AC
b) Sửa đề: ∆IBE ∽ ∆ICH
∆ACE vuông tại E
⇒ ∠BCE + ∠BCA = 90⁰
⇒ ∠BCE + ∠ICH = 90⁰
∆BCE vuông tại E
⇒ ∠BCE + ∠CBE = 90⁰
⇒ ∠BCE + ∠IBE = 90⁰
Mà ∠BCE + ∠ICH = 90⁰ (cmt)
⇒ ∠IBE = ∠ICH
Xét ∆IBE và ∆ICH có:
∠BIE = ∠CIH (đối đỉnh)
∠IBE = ∠ICH (cmt)
⇒ ∆IBE ∽ ∆ICH (g-g)
c) Do ABCD là hình bình hành (gt)
⇒ AB // CD và AD // BC
⇒ AB // CQ
Theo hệ quả của định lý Thales
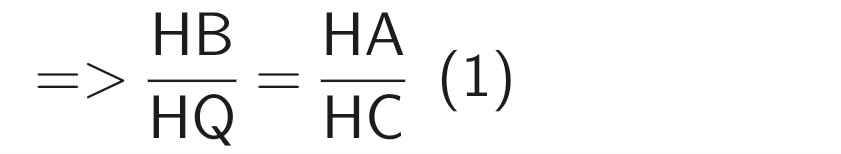
Do AD // BC (cmt)
⇒ AK // BC
Theo hệ quả của định lý Thales
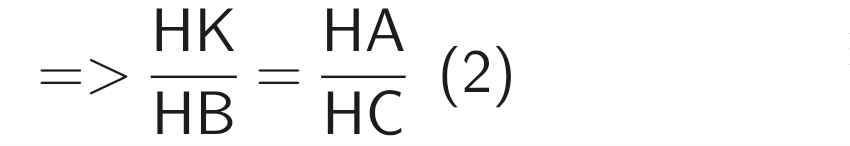 Từ (1) và (2)
Từ (1) và (2)
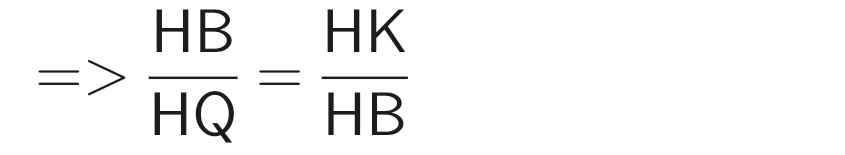 ⇒ HB.HB = HK.HQ
⇒ HB.HB = HK.HQ
Hay BH.BH = HK.HQ

Lời giải:
$\frac{1}{a}+\frac{1}{b}+\frac{1}{c}=0$
$\Rightarrow \frac{ab+bc+ac}{abc}=0$
$\Rightarrow ab+bc+ac=0$
Đặt $ab=x, bc=y, ca=z$ thì $x+y+z=0$
$\Rightarrow x+y=-z$.
Khi đó:
$A=\frac{b^3c^3+c^3a^3+a^3c^3}{(abc)^2}=\frac{x^3+y^3+z^3}{xyz}$
$=\frac{(x+y)^3-3xy(x+y)+z^3}{xyz}$
$=\frac{(-z)^3-3xy(-z)+z^3}{xyz}=\frac{-z^3+3xyz+z^3}{xyz}=\frac{3xyz}{xyz}=3$

\(x^4+2x^2+1=\left(x^2\right)^2+2x^2+1=\left(x^2+1\right)^2\)

a/
$A=x^2-4x+10=(x^2-4x+4)+6=(x-2)^2+6$
Ta thấy:
$(x-2)^2\geq 0$ với mọi $x\in\mathbb{R}$
$\Rightarrow A=(x-2)^2+6\geq 6>0$ với mọi $x\in\mathbb{R}$
$\Rightarrow A$ luôn có giá trị dương với mọi giá trị $x$.
a/
$B=2x^2-2x+3=x^2+(x^2-2x+1)+2=x^2+(x-1)^2+2$
Ta thấy:
$x^2\geq 0; (x-1)^2\geq 0$ với mọi $x\in\mathbb{R}$
$\Rightarrow B=x^2+(x-1)^2+2\geq 2>0$ với mọi $x\in\mathbb{R}$
$\Rightarrow B$ luôn có giá trị dương với mọi giá trị $x$.
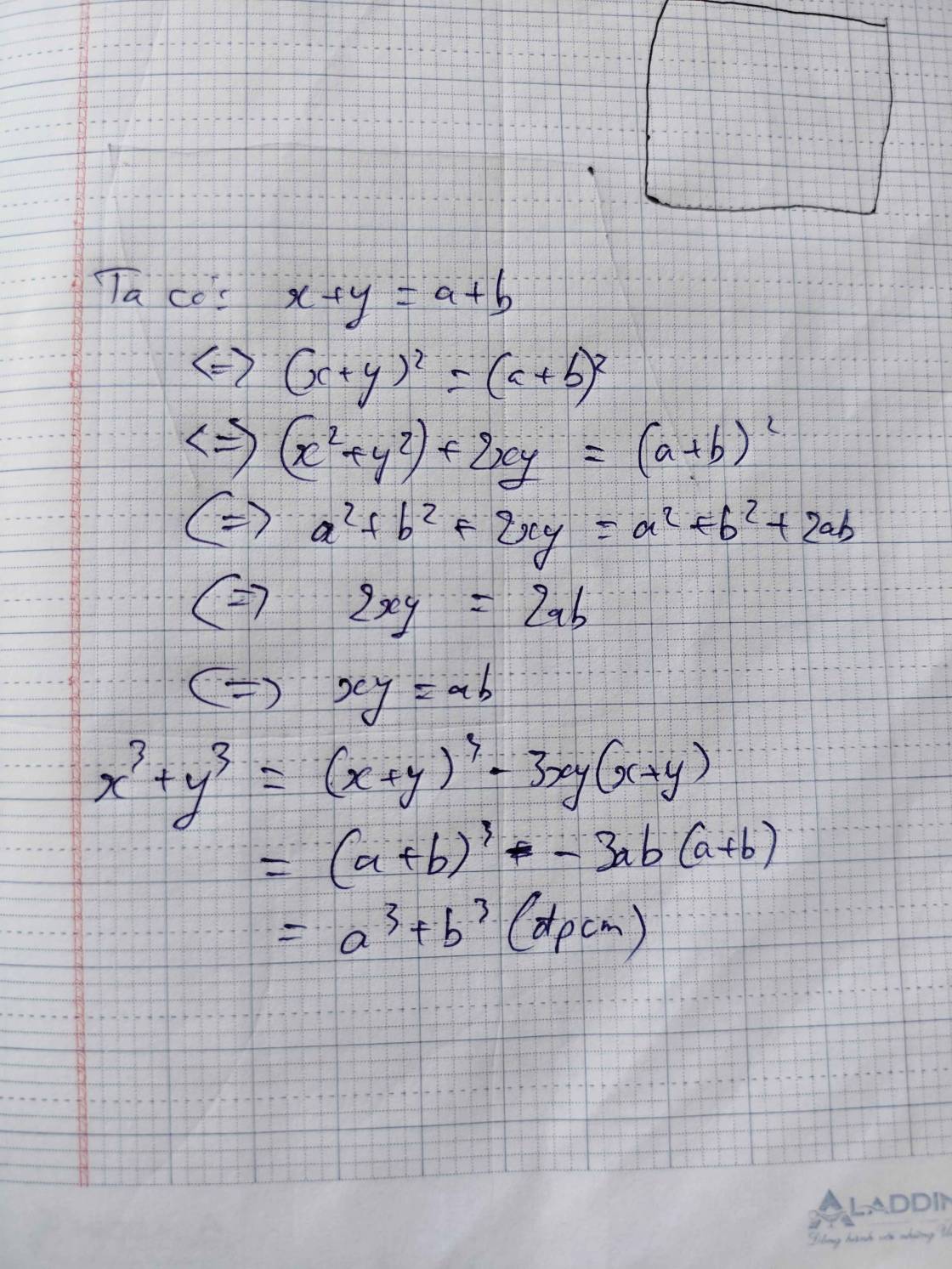

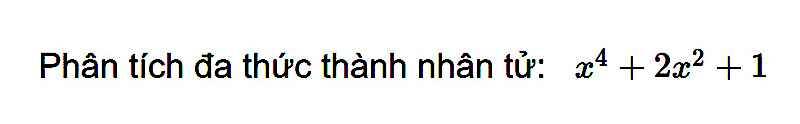

a: Ta có: \(MB=MC=\dfrac{BC}{2}\)
\(NA=ND=\dfrac{AD}{2}\)
\(BA=CD=\dfrac{BC}{2}\)
Do đó: MB=MC=NA=ND=BA=CD
Xét tứ giác BMDN có
BM//DN
BM=DN
Do đó: BMDN là hình bình hành
b: Xét tứ giác BMNA có
BM//NA
BM=NA
Do đó: BMNA là hình bình hành
Xét hình bình hành BMNA có BM=BA
nên BMNA là hình thoi
=>BN\(\perp\)AM tại P và P là trung điểm chung của AM và BN
Xét tứ giác CMDN có
CM//DN
CM=DN
Do đó: CMND là hình bình hành
Hình bình hành CMND có CM=CD
nên CMND là hình thoi
=>CN\(\perp\)MD tại Q và Q là trung điểm chung của DM và CN
Xét ΔMAD có
MN là đường trung tuyến
\(MN=\dfrac{AD}{2}\left(=AB\right)\)
Do đó: ΔMAD vuông tại M
Xét tứ giác PMQN có
\(\widehat{PNQ}=\widehat{MPN}=\widehat{MQN}\left(=90^0\right)\)
nên PMQN là hình chữ nhật
c: Để PMQN là hình chữ nhật thì PM=PN
=>AM=BN
Hình thoi ABMN có AM=BN
nên ABMN là hình vuông
=>\(\widehat{ABC}=90^0\)
d: \(AD=2\cdot AB=4\left(cm\right)\)
Xét ΔMAD vuông tại M có \(sinMAD=\dfrac{MD}{AD}\)
=>\(\dfrac{MD}{4}=sin30=\dfrac{1}{2}\)
=>MD=2(cm)
=>MQ=1(cm)
MN=AB
=>MN=2(cm)
ΔMNQ vuông tại Q
=>\(MQ^2+QN^2=MN^2\)
=>\(QN=\sqrt{3}\left(cm\right)\)
Diện tích tứ giác PMQN là:
\(S_{PMQN}=\sqrt{3}\cdot1=\sqrt{3}\left(cm^2\right)\)