(0,8)^5:(0,4)^6
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\left(\dfrac{11}{4}\right)^{12}:\left(-\dfrac{11}{4}\right)^{11}\)
\(=\left(-\dfrac{11}{4}\right)^{12}:\left(-\dfrac{11}{4}\right)^{11}\)
\(=\left(-\dfrac{11}{4}\right)^{12-11}\)
\(=\left(-\dfrac{11}{4}\right)^1\)
\(=-\dfrac{11}{4}\)

\(\left(\dfrac{3}{7}\right)^2.\left(-7\right)^4\\ =\left(\dfrac{3}{7}\right)^2.7^4\\ =\left(\dfrac{3}{7}\right)^2.7^2.7^2\\ =9.49\\ =441\)

Vì \(\dfrac{1}{11}>\dfrac{1}{18}>\dfrac{1}{21}>\dfrac{1}{24}>\dfrac{1}{27}>\dfrac{1}{29}\)
\(\Rightarrow\dfrac{1}{11}+\dfrac{1}{11}+\dfrac{1}{11}+\dfrac{1}{11}+\dfrac{1}{11}+\dfrac{1}{11}+\dfrac{1}{11}>\dfrac{1}{4}+\dfrac{1}{11}+\dfrac{1}{18}+\dfrac{1}{21}+\dfrac{1}{24}+\dfrac{1}{27}+\dfrac{1}{29}\)\(\dfrac{1}{11}+\dfrac{1}{11}+\dfrac{1}{11}+\dfrac{1}{11}+\dfrac{1}{11}+\dfrac{1}{11}+\dfrac{1}{11}=\dfrac{1}{11}.7=\dfrac{7}{11}\)
Ta có:
\(\dfrac{7}{11}=\dfrac{7.5}{11.5}=\dfrac{35}{55};\dfrac{4}{5}=\dfrac{4.11}{5.11}=\dfrac{44}{55}\)
\(Vì\) \(\dfrac{44}{55}>\dfrac{35}{55}\)
\(\Rightarrow\dfrac{4}{5}>\dfrac{7}{11}\)
\(\Rightarrow\dfrac{1}{4}+\dfrac{1}{11}+\dfrac{1}{18}+\dfrac{1}{21}+\dfrac{1}{24}+\dfrac{1}{27}+\dfrac{1}{29}< \dfrac{4}{5}\left(đpcm\right)\)
Ta thấy :
\(\dfrac{1}{4}+\dfrac{1}{11}< \dfrac{1}{4}+\dfrac{1}{4}=\dfrac{1}{2}=1-\dfrac{1}{2}\)
\(\dfrac{1}{18}+\dfrac{1}{21}< \dfrac{1}{12}+\dfrac{1}{12}=\dfrac{1}{6}=\dfrac{1}{2}-\dfrac{1}{3}\)
\(\dfrac{1}{24}+\dfrac{1}{27}< \dfrac{1}{24}+\dfrac{1}{24}=\dfrac{1}{12}=\dfrac{1}{3}-\dfrac{1}{4}\)
\(\dfrac{1}{29}< \dfrac{1}{20}=\dfrac{1}{4}-\dfrac{1}{5}\)
\(\Rightarrow\dfrac{1}{4}+\dfrac{1}{11}+\dfrac{1}{18}+\dfrac{1}{21}+\dfrac{1}{24}+\dfrac{1}{27}+\dfrac{1}{29}< 1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{5}\)
\(\Rightarrow\dfrac{1}{4}+\dfrac{1}{11}+\dfrac{1}{18}+\dfrac{1}{21}+\dfrac{1}{24}+\dfrac{1}{27}+\dfrac{1}{29}< 1-\dfrac{1}{5}=\dfrac{4}{5}\)
\(\Rightarrow dpcm\)

a) \(a\left(b+1\right)=3\left(a;b\inℤ\right)\)
\(\Rightarrow a;\left(b+1\right)\in U\left(3\right)=\left\{-1;1;-3;3\right\}\)
\(\Rightarrow\left(a;b\right)\in\left\{\left(-1;-4\right);\left(1;2\right);\left(-3;-2\right);\left(3;0\right)\right\}\)
b) \(2n+7⋮n+1\left(n\inℤ\right)\)
\(\Rightarrow2n+7-2\left(n+1\right)⋮n+1\)
\(\Rightarrow2n+7-2n-2⋮n+1\)
\(\Rightarrow5⋮n+1\)
\(\Rightarrow n+1\in U\left(5\right)=\left\{-1;1;-5;5\right\}\)
\(\Rightarrow n\in\left\{-2;0;-6;4\right\}\)
c) \(xy+x-y=6\left(x;y\inℤ\right)\)
\(\Rightarrow x\left(y+1\right)-y-1+1=6\)
\(\Rightarrow x\left(y+1\right)-\left(y+1\right)=5\)
\(\Rightarrow\left(x-1\right)\left(y+1\right)=5\)
\(\Rightarrow\left(x-1\right);\left(y+1\right)\in U\left(5\right)=\left\{-1;1;-5;5\right\}\)
\(\Rightarrow\left(x;y\right)\in\left\{\left(-0;-6\right);\left(2;4\right);\left(-4;-2\right);\left(6;0\right)\right\}\)

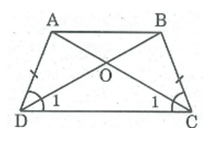
Xét \(\Delta ADC\) và \(\Delta BCD\) có:
\(AD=BC\left(gt\right)\)
\(\widehat{ADC}=\widehat{BCD}\left(gt\right)\)
Cạnh \(DC\) là cạnh chung
Vậy \(\Delta ADC=\Delta BCD\left(c.g.c\right)\)
\(\Rightarrow\widehat{C1}=\widehat{D1}\) ( 2 góc tưng ứng )
Trong \(\Delta OCB\) ta có: \(\widehat{C1}=\widehat{D1}\left(CMT\right)\)
\(\Rightarrow\Delta OCB\) cân tại \(O\)
\(\Rightarrow OC=OD\) ( cạnh tương ứng ) \(\left(1\right)\)
\(\Rightarrow AC=BD\) ( tính chất hình thang cân )
\(\Rightarrow AO+OC=BO+OD\left(2\right)\)
Từ \(\left(1\right)\) và \(\left(2\right)\) suy ra \(AO=BO\)

Đề bài ra khi chia tử và mẫu ta được số \(0\) \(abc\) nên phân số có dạng:
\(\dfrac{abc}{999}\)
Ta có:
\(\dfrac{abc}{999}=\dfrac{abc}{3^3.37}=\dfrac{abc.37^2}{\left(3.37\right)^2}\)
Vì phân số này bằng lập phương của phân số khác nên \(abc.37^2\)
\(=\left(d.37\right)^3\Rightarrow abc=37d^3\)
Mặt \(\ne\) \(0< abc< 999\Rightarrow37d^3< 999\Rightarrow d^3< 27\)
\(\Leftrightarrow d=3\)
Với \(d=1\) thì \(abc=037\Rightarrow\) phân số cần tìm là: \(\dfrac{037}{999}=\dfrac{1}{27}\)
Với \(d=2\) thi \(abc=296\Rightarrow\) phân số cần tìm là: \(\dfrac{296}{999}=\dfrac{8}{27}\)
Không mất tổng quát, giả sử cả tử và mẫu của phân số cần tìm đều dương.
Gọi phân số đó là \(\dfrac{m}{n}\) với \(m,n\inℕ^∗\), \(m< n\) và \(ƯCLN\left(m,n\right)=1\).
Theo đề bài, ta có: \(\dfrac{m}{n}=\left(\dfrac{a}{b}\right)^3\) (với \(a< b\inℕ^∗\) và \(ƯCLN\left(a,b\right)=1\))
Và \(\dfrac{m}{n}=0,\overline{xyzxyzxyz...}\) \(=\dfrac{x}{10^1}+\dfrac{y}{10^2}+\dfrac{z}{10^3}+\dfrac{x}{10^4}+...\)
\(=x\left(\dfrac{1}{10^1}+\dfrac{1}{10^4}+...\right)+y\left(\dfrac{1}{10^2}+\dfrac{1}{10^5}+...\right)+z\left(\dfrac{1}{10^3}+\dfrac{1}{10^6}+...\right)\)
Ta sẽ rút gọn tổng \(S_1=\dfrac{1}{10^1}+\dfrac{1}{10^4}+...\)
Có \(1000S_1=100+\dfrac{1}{10^1}+...\)
\(\Rightarrow999S_1=100\) \(\Rightarrow S_1=\dfrac{100}{999}\)
Có \(S_2=\dfrac{1}{10^2}+\dfrac{1}{10^5}+...\)
\(\Rightarrow1000S_2=10+\dfrac{1}{10^2}+...\)
\(\Rightarrow999S_2=10\Rightarrow S_2=\dfrac{10}{999}\)
Lại có \(S_3=\dfrac{1}{10^3}+\dfrac{1}{10^6}+...\)
\(\Rightarrow1000S_3=1+\dfrac{1}{10^3}+...\)
\(\Rightarrow999S_3=1\Rightarrow S_3=\dfrac{1}{999}\)
Từ đó ta có \(\dfrac{m}{n}=\dfrac{100x+10y+z}{999}=\dfrac{\overline{xyz}}{999}\), suy ra \(\overline{xyz}< 999\)
Vì \(999=3^3.37\) nên để phân số có thể viết thành lập phương của 1 phân số khác thì \(\overline{xyz}⋮37\). Gọi phân số sau khi rút gọn \(\dfrac{m}{n}\) cho 37 là \(\dfrac{k}{27}\). Khi đó vì \(k\) là 1 lập phương đúng của 1 số nguyên nhỏ hơn 27 nên \(k\in\left\{1,8\right\}\). Thử lại, cả 2 trường hợp đều thỏa mãn.
Vậy các phân số cần tìm là \(\dfrac{1}{27}\) và \(\dfrac{8}{27}\).

Hôm nay olm.vn sẽ hướng dẫn các em giải toán nâng cao lớp 7 bằng phương pháp hệ số bất định em nhé.
Vì ( \(x^3\) - \(x^2\) + a\(x\) + b): (\(x^2\) - 2\(x\) + 3) dư 6
Ta thấy đa thức bị chia bậc ba, đa thức chia bậc hai nên thương có dạng: c\(x\) + d vì hệ số cao nhất của đa thức bị chia là 1 nên c = 1
Theo bài ra ta có:
\(x^3\) - \(x^2\) + a\(x\) + b = (\(x^2\) - 2\(x\) + 3)(\(x\) + d) + 6
\(x^3\) - \(x^2\) + a\(x\) + b = \(x^3\) + d\(x^2\) - 2\(x^2\) - 2d\(x\) + 3\(x\) + 3d + 6
\(x^3\) - \(x^2\) + a\(x\) + b = \(x^{3^{ }}\) + (d - 2)\(x^2\) + (3 - 2d)\(x\) + 3d + 6
⇒ \(\left\{{}\begin{matrix}d-2=-1\\a=3-2d\\b=3d+6\end{matrix}\right.\)⇒\(\left\{{}\begin{matrix}d=1\\a=3-2\\b=3+6\end{matrix}\right.\) ⇒ \(\left\{{}\begin{matrix}d=1\\a=1\\b=9\end{matrix}\right.\)
Vậy a = 1; b = 9


a, \(\dfrac{\dfrac{-6}{7}+\dfrac{6}{19}-\dfrac{6}{31}}{\dfrac{9}{7}-\dfrac{9}{19}+\dfrac{9}{31}}\)
= \(\dfrac{-6.\left(\dfrac{1}{7}-\dfrac{1}{19}+\dfrac{1}{31}\right)}{9.\left(\dfrac{1}{7}-\dfrac{1}{19}+\dfrac{1}{31}\right)}\)
= - \(\dfrac{2}{3}\)
b, \(\dfrac{\dfrac{1}{9}-\dfrac{1}{7}-\dfrac{1}{11}}{\dfrac{4}{9}-\dfrac{4}{7}-\dfrac{4}{11}}\)+ \(\dfrac{\dfrac{3}{5}-\dfrac{3}{25}-\dfrac{3}{125}-\dfrac{3}{625}}{\dfrac{4}{5}-\dfrac{4}{25}-\dfrac{4}{125}-\dfrac{4}{625}}\)
= \(\dfrac{\dfrac{1}{9}-\dfrac{1}{7}-\dfrac{1}{11}}{4.(\dfrac{1}{9}-\dfrac{1}{7}-\dfrac{1}{11})}\) + \(\dfrac{3.(\dfrac{1}{5}-\dfrac{1}{25}-\dfrac{1}{125}-\dfrac{1}{625})}{4.\left(\dfrac{1}{5}-\dfrac{1}{25}-\dfrac{1}{125}-\dfrac{1}{625}\right)}\)
= \(\dfrac{1}{4}\) + \(\dfrac{3}{4}\)
= 1
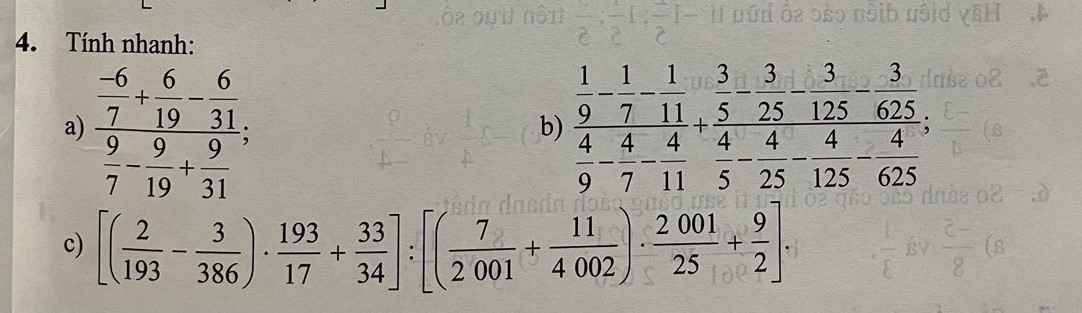
(0,8)⁵ : (0,4)⁶
= (4/5)⁵ : (2/5)⁶
= 1024/3125 : 64/15625
= 16 . 5
= 80
\(\left(0,8\right)^5:\left(0,4\right)^6\\ =\left(\dfrac{4}{5}\right)^5:\left(\dfrac{2}{5}\right)^6\\ =\dfrac{1024}{3125}:\dfrac{64}{15625}\\ =16.5\\ =80\)