Có 3 số hữu tỉ dương là \(0,15;\dfrac{-6}{-11}=\dfrac{6}{11};\dfrac{25}{14}\)

Chọn C

-3^7.2^8/2^.3^7

=-3.2

=-6

5^3.3^5/5^3(0,5+2,5)

=5^3.3^5/5^3.3\

3^4

=81

5.7^4+7^3.25/7^5.125-7^3.50

=5.7^3(7+5

5.7^4+7^3.25/7^5.125-7^3.50

=5.7^4+7^3.5^2/7^5.5^3-7^3.11.5

=5.7^3(1.7+1.5)/7^3.5(7^2.25-11)

12/1250

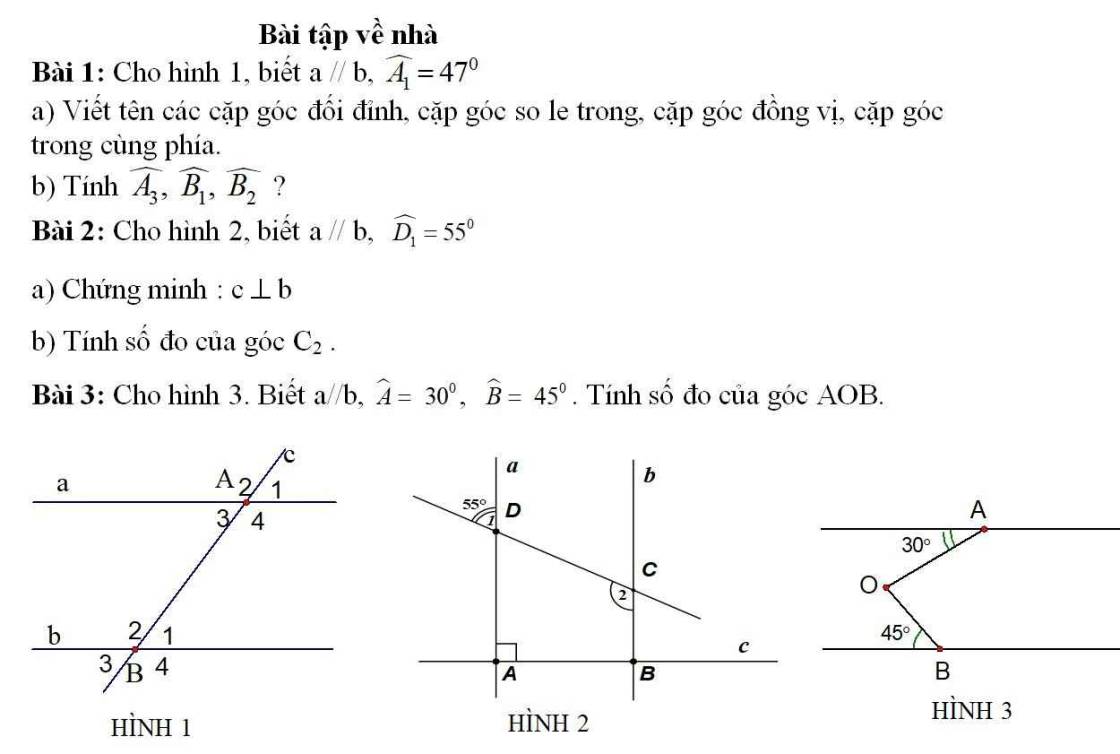
 Kéo dài tia AO và đặt là Ax. Khi đó:

\(\widehat{BOC}=\widehat{BOx}+\widehat{COx}\)

 Xét tam giác OAB có \(\widehat{BOx}\) là góc ngoài tại O nên 

\(\widehat{BOx}=\widehat{A_1}+\widehat{ABO}\) (1)

 Tương tự, ta có \(\widehat{COx}=\widehat{A_2}+\widehat{ACO}\) (2)

 Cộng theo vế (1) và (2), ta được:

 \(\widehat{BOC}=\widehat{A_1}+\widehat{A_2}+\widehat{ABO}+\widehat{ACO}\)

        \(=\widehat{A}+\widehat{ABO}+\widehat{ACO}\)

 Ta có đpcm.

Cho \(A=\left(-\dfrac{4}{7}\right)^3\times\left(-\dfrac{4}{7}\right)^4\times\left(\dfrac{4}{7}\right)^5\)

\(A=\left(-\dfrac{4}{7}\right)^{3+4}\times\left(\dfrac{4}{7}\right)^5\)

\(A=\left(-\dfrac{4}{7}\right)^7\times\left(\dfrac{4}{7}\right)^5\)

\(-A=-\left[\left(-\dfrac{4}{7}\right)^7\times\left(\dfrac{4}{7}\right)^5\right]\)

\(-A=\left(-\dfrac{4}{7}\right)^7\times\left(-\dfrac{4}{7}\right)^5\)

\(-A=\left(-\dfrac{4}{7}\right)^{7+5}\)

\(-A=\left(-\dfrac{4}{7}\right)^{12}\)

\(A=-\left(\dfrac{4}{7}\right)^{12}\)

Sao tìm x lại đặt A?

A = \(\dfrac{1+5+5^2+5^3+5^4+...+5^{17}}{1+5^2+5^4+...+5^{16}}\)

Đặt tử số là B = 1 + 5 + 5² + 5³ + 5⁴ +...+ 5¹⁷

                  5B =       5 + 5² + 5³ + 5⁴ +...+ 5¹⁷ + 5¹⁸

                  5B - B = 5¹⁸ - 1

                  4B       = 5¹⁸ - 1

                    B       = (5¹⁸ - 1) : 4

Đặt mẫu số là C  = 1 + 5² + 5⁴ +...+ 5¹⁶

                    5².C =       5² + 5⁴ +...+ 5¹⁶ + 5¹⁸

                    25.C - C  =  5¹⁸ - 1

                    24C         =   5¹⁸ - 1

                        C         =    (5¹⁸ - 1): 24 

A = \(\dfrac{B}{C}\) = \(\dfrac{\dfrac{5^{18}-1}{4}}{\dfrac{5^{18}-1}{24}}\)

A = 6 

a=6 banj nha

\(\Leftrightarrow x^2-xy-5x+4y+9=0\)

\(\Leftrightarrow\left(x^2-xy\right)-\left(4x-4y\right)-x+9=0\)

\(\Leftrightarrow x\left(x-y\right)-4\left(x-y\right)-x+9=0\)

\(\Leftrightarrow\left(x-y\right)\left(x-4\right)-\left(x-4\right)+5=0\)

\(\Leftrightarrow\left(x-4\right)\left(x-y-1\right)=-5\)

Do \(x;y\in Z\Rightarrow\left(x-4\right);\left(x-y-1\right)\in Z\)

Ta có các trường hợp sau

+ TH1:

\(\left\{{}\begin{matrix}x-4=1\\x-y-1=-5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=5\\y=9\end{matrix}\right.\)

+ TH2:

\(\left\{{}\begin{matrix}x-4=-1\\x-y-1=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=3\\y=-3\end{matrix}\right.\)

+ TH3:

\(\left\{{}\begin{matrix}x-4=5\\x-y-1=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=9\\y=9\end{matrix}\right.\)

+ TH4:

\(\left\{{}\begin{matrix}x-4=-5\\x-y-1=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-1\\y=-3\end{matrix}\right.\)

Dễ vãi