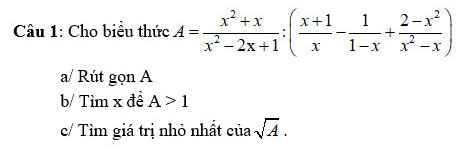
giúp mình câu c thôi nhé.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Lời giải:
Chu vi đáy: $2.8\pi=16\pi$ (cm)
Diện tích xung quanh: $16\pi.10=160$ (cm2)
Diện tích đáy: $8^2\pi =64\pi$ (cm2)
Thể tích hình trụ: $64\pi.10=640\pi$ (cm3)

Theo đề bài ta có:
\(x_0+x_1=-a_1;x_0.x_1=b_1\)
\(x_0+x_2=-a_2;x_0.x_2=b_2\)
............................................
\(x_0+x_{2022}=-a_{2022};x_0.x_{2022}=b_{2022}\)
Ta có:
\(x_0+\alpha=x_0+\dfrac{x_1+x_2+...+x_{2022}}{2022}=\dfrac{\left(x_0+x_1\right)+\left(x_0+x_2\right)+...+\left(x_0+x_{2022}\right)}{2022}=-\dfrac{a_1+a_2+...+a_{2022}}{2022}\)\(x_0\alpha=x_0\dfrac{x_1+x_2+...+x_{2022}}{2022}=\dfrac{x_0x_1+x_0x_2+...+x_0x_{2022}}{2022}=\dfrac{b_1+b_2+...+b_{2022}}{2022}\)
Từ đây ta có được \(x_0;\alpha\)là 2 nghiệm của phương trình
\(x^2+\dfrac{a_1+a_2+...+a_{2022}}{2022}x+\dfrac{b_1+b_2+...+b_{2022}}{2022}=0\)

Bạn tự vẽ hình nhé. Mình tóm tắt cách giải:
1) Dễ thấy \(\widehat{BFC}=\widehat{BEC}=90^o\) nên tứ giác BFEC nội tiếp (2 đỉnh kề nhau cùng nhìn cạnh đối diện dưới 1 góc vuông)
2) Ta thấy \(\widehat{ABD}=90^o\) (góc nội tiếp chắn nửa đường tròn) \(\Rightarrow BD\perp AB\)
Lại có \(CH\perp AB\left(gt\right)\) nên \(BD//CH\)
Tương tự, ta dễ dàng chứng minh được \(CD//BH\)
Do đó tứ giác BHCD là hình bình hành \(\Rightarrow\) 2 đường chéo BC và DH cắt nhau tại trung điểm của mỗi đoạn.
Mà HD cắt BC tại M (gt) nên M là trung điểm của đoạn BC.
3) Sửa lại đề là \(AD\perp EF\) nhé
Kẻ tiếp tuyến Ax của (O) thuộc nửa mặt phẳng bờ OA chứa điểm B. Dễ thấy rằng \(\widehat{BAx}=\widehat{ACB}\) (góc tạo bởi tiếp tuyến và dây cung và góc nội tiếp cùng chắn \(\stackrel\frown{AB}\))
Tứ giác BFEC nội tiếp (cmt) \(\Rightarrow\widehat{AFE}=\widehat{ACB}\) (góc ngoài tại 1 đỉnh bằng góc trong tại đỉnh đối diện)
Từ đó \(\widehat{BAx}=\widehat{AFE}\) dẫn đến \(Ax//EF\) (2 góc so le trong bằng nhau)
Mà \(Ax\perp OA\) (do Ax là tiếp tuyến tại A của (O))
\(\Rightarrow OA\perp EF\) hay \(AD\perp EF\) (đpcm)
4)

Thông thường dạng bài tìm GTNN mà có điều kiện \(a+2b\ge k\) (\(k\) là 1 hằng số) thì điểm rơi sẽ bằng \(a=2b=\dfrac{k}{2}\) hay \(a=\dfrac{k}{2};b=\dfrac{k}{4}\)
thì suy ra cái số đằng sau dấu nhỏ hơn hoặc bằng đó là giá trị nhỏ nhất

Điều kiện: \(x\ge0\)
+ Nếu \(\sqrt{x}-4>0\Leftrightarrow\sqrt{x}>4\Leftrightarrow x>16\)
\(A\Leftrightarrow\sqrt{x}-2< \sqrt{x}-4\Leftrightarrow-2< -4\) (vô lý)
+ Nếu \(\sqrt{x}-4< 0\Leftrightarrow x< 16\)
\(A\Leftrightarrow\sqrt{x}-2>\sqrt{x}-4\Leftrightarrow-2>-4\forall x\)
=> A đúng với mọi x<16
\(A=\dfrac{x^2}{x-1}\) ( x khác { 0;\(\pm\)1} )
\(\sqrt{A}\) xác định <=> A>=0
=> x > 1
\(A=x+1+\dfrac{1}{x-1}=\left(x-1+\dfrac{1}{x-1}\right)+2>=2\sqrt{\left(x-1\right).\dfrac{1}{x-1}}+2=4\)
=> \(\sqrt{A}\) >= 2
Vậy giá trị nhỏ nhất của \(\sqrt{A}\) là : 2 khi x = 2