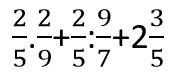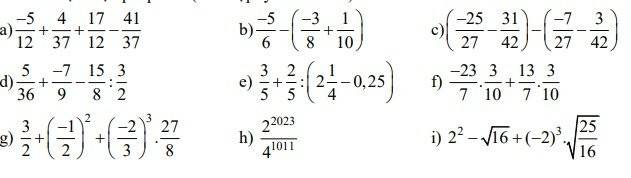Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
$=\frac{2}{5}\times \frac{2}{9}+\frac{2}{5}\times \frac{7}{9}+2\frac{3}{5}$
$=\frac{2}{5}\times (\frac{2}{9}+\frac{7}{9})+2+\frac{3}{5}$
$=\frac{2}{5}\times 1+2+\frac{3}{5}=\frac{2}{5}+\frac{3}{5}+2=1+2=3$

Trước tiên, ta chứng minh \(\dfrac{1}{a}+\dfrac{1}{b}\ge\dfrac{4}{a+b}\) với \(a,b>0\) (*)
(*) \(\Leftrightarrow\dfrac{a+b}{ab}\ge\dfrac{4}{a+b}\)
\(\Leftrightarrow\left(a+b\right)^2\ge4ab\)
\(\Leftrightarrow a^2+2ab+b^2\ge4ab\)
\(\Leftrightarrow a^2-2ab+b^2\ge0\)
\(\Leftrightarrow\left(a-b\right)^2\ge0\), luôn đúng.
Vậy (*) được chứng minh. Dấu "=" xảy ra \(\Leftrightarrow a=b\)
\(\Rightarrow VT=a+b+\dfrac{1}{a}+\dfrac{1}{b}\ge a+b+\dfrac{4}{a+b}\)
Đặt \(a+b=t\left(0< t\le\dfrac{1}{2}\right)\)thì
\(VT\ge t+\dfrac{4}{t}\) \(=t+\dfrac{1}{4t}+\dfrac{15}{4t}\) (1)
Bây giờ ta sẽ chứng minh \(a+b\ge2\sqrt{ab}\) với \(a,b>0\) (**)
(**) \(\Leftrightarrow a-2\sqrt{ab}+b\ge0\)
\(\Leftrightarrow\left(\sqrt{a}\right)^2-2\sqrt{a}\sqrt{b}+\left(\sqrt{b}\right)^2\ge0\)
\(\Leftrightarrow\left(\sqrt{a}-\sqrt{b}\right)^2\ge0\) (luôn đúng)
Vậy (**) được chứng minh. Dấu "=" xảy ra \(\Leftrightarrow a=b\)
Do đó từ (1) \(\Rightarrow VT\ge\left(t+\dfrac{1}{4t}\right)+\dfrac{15}{4t}\)
\(\ge2\sqrt{t.\dfrac{1}{4}t}+\dfrac{15}{4.\dfrac{1}{2}}\) (do \(0< t\le\dfrac{1}{2}\))
\(=\dfrac{17}{2}\)
Dấu "=" xảy ra \(\Leftrightarrow\left\{{}\begin{matrix}t=a+b=\dfrac{1}{2}\\a=b\end{matrix}\right.\Leftrightarrow a=b=\dfrac{1}{4}\)
Ta có đpcm.

Lời giải:
$2023xy+2024yz+4047xz=2023xy+2024y(-x-y)+4047x(-x-y)$
$=-2024y^2-4047x^2-4048xy$
$=-[4047x^2+2024y^2+4048xy]$
$=-[2024(x^2+y^2+2xy)+2023x^2]=-[2024(x+y)^2+2023x^2]$
Vì $2024(x+y)^2+2023x^2\geq 0$ với mọi $x,y$
$\Rightarrow -[2024(x+y)^2+2023x^2]\leq 0$ với mọi $x,y$
Do đó nó không thể nhận giá trị dương.

a.
\(=(\frac{-5}{12}+\frac{17}{12})+(\frac{4}{37}+\frac{-41}{37})=\frac{12}{12}+\frac{-37}{37}=1+(-1)=0\)
b.
\(=\frac{-20}{24}+\frac{9}{24}-\frac{1}{10}=\frac{-11}{24}+\frac{1}{10}=\frac{-43}{120}\)
c.
\(=\frac{-25}{27}-\frac{31}{42}+\frac{7}{27}+\frac{3}{42}\\ =\frac{-25}{27}+\frac{7}{27}+(\frac{-31}{42}+\frac{3}{42})\\ =\frac{-2}{3}+\frac{-2}{3}=\frac{-4}{3}\)
d.
\(=\frac{5}{36}+\frac{-28}{36}-\frac{5}{4}=\frac{5}{36}+\frac{-28}{36}-\frac{45}{36}\\ =\frac{-68}{36}=\frac{-17}{9}\)
e.
\(=\frac{3}{5}+\frac{2}{5}: 2=\frac{3}{5}+\frac{1}{5}=\frac{4}{5}\)
f.
\(=\frac{3}{10}(\frac{-23}{7}+\frac{13}{7})=\frac{3}{10}.\frac{-10}{7}=\frac{-3}{7}\)
g.
\(=\frac{3}{2}+\frac{1}{4}+(-1)=\frac{7}{4}-1=\frac{3}{4}\)
h.
\(=\frac{2^{2023}}{(2^2)^{1011}}=\frac{2^{2023}}{2^{2022}}=2^{2023-2022}=2\)
i.
\(=4-4+(-8).\frac{5}{4}=0+(-10)=-10\)

Để A có giá trị là một số nguyên thì:
\(\left(\sqrt{x}+1\right)⋮\left(\sqrt{x}-3\right)\)
\(\Leftrightarrow\left(\sqrt{x}-3\right)+4⋮\left(\sqrt{x}-3\right)\)
\(\Leftrightarrow4⋮\left(\sqrt{x}-3\right)\)
Vì \(x\in Z\) nên \(\left(\sqrt{x}-3\right)\inƯ\left(4\right)=\left\{\pm1,\pm2,\pm4\right\}\)
Ta có bảng sau:
| \(\sqrt{x}-3\) | 1 | -1 | 2 | -2 | 4 | -4 |
| \(\sqrt{x}\) | 4 | 2 | 5 | 1 | 7 | -1 |
| x | 16 | 4 | 25 | 1 | 49 | (loại) |
Vậy ....
Ta có: \(A=\dfrac{\sqrt{x}+1}{\sqrt{x}-3}=\dfrac{\left(\sqrt{x}-3\right)+4}{\sqrt{x}-3}=\dfrac{\sqrt{x}-3}{\sqrt{x}-3}=\dfrac{4}{\sqrt{x}-3}=1+\dfrac{4}{\sqrt{x}-3}\)
Để A có giá trị là một số nguyên khi:
\(4⋮\sqrt{x}-3\) hay \(\sqrt{x}-3\inƯ\left(4\right)=\left\{\pm1;\pm2;\pm4\right\}\)
Do đó:
\(\sqrt{x}-3=-1\Rightarrow\sqrt{x}=-1+3=2\Rightarrow x=4\)
\(\sqrt{x}-3=1\Rightarrow\sqrt{x}=1+3=4\Rightarrow x=16\)
\(\sqrt{x}-3=-2\Rightarrow\sqrt{x}=-2+3=1\Rightarrow x=1\)
\(\sqrt{x}-3=2\Rightarrow\sqrt{x}=2+3=5\Rightarrow x=25\)
\(\sqrt{x}-3=-4\Rightarrow\sqrt{x}=-4+3=-1\) ( loại )
\(\sqrt{x}-3=4\Rightarrow\sqrt{x}=4+3=7\Rightarrow x=49\)
Vậy để A là một số nguyên khi \(x\in\left\{4;16;1;25;49\right\}\)