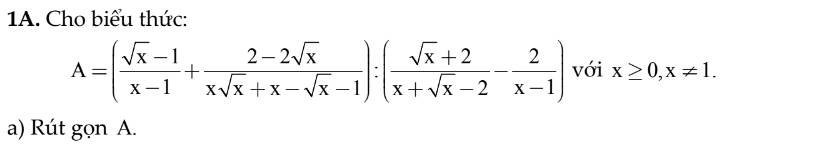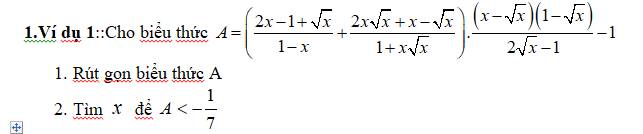
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\sqrt{4+\sqrt{5\sqrt{3}+5\sqrt{48-10\sqrt{\left(2+\sqrt{3}\right)^2}}}}\)
\(=\sqrt{4+\sqrt{5\sqrt{3}+5\sqrt{28-10\sqrt{3}}}}\)
\(=\sqrt{4+\sqrt{5\sqrt{3}+5\sqrt{\left(5-\sqrt{3}\right)^2}}}=\sqrt{4+\sqrt{5\sqrt{3}+25-5\sqrt{3}}}\)
\(=\sqrt{4+\sqrt{25}}=\sqrt{4+5}=\sqrt{9}=3\)
\(\sqrt{4+5\sqrt{3}+5\sqrt{48-10\sqrt{7+4\sqrt{3}}}}\)
\(=\sqrt{4+\sqrt{5\sqrt{3}+5\sqrt{48-10(\sqrt{3+2})^2}}}\)
\(=\sqrt{4+\sqrt{5\sqrt{3}+5\sqrt{48-10\sqrt{3}-20}}}\)
\(=\sqrt{4+\sqrt{5\sqrt{3}+5\sqrt{(5-\sqrt{3})^2}}}\)
\(=\sqrt{4+\sqrt{5\sqrt{3}+25-5\sqrt{3}}}\)
\(=\sqrt{4+\sqrt{25}}\)
\(=\sqrt{4+5}=3\)

a, đk x >= 0
\(\Leftrightarrow\sqrt{x}=7\Leftrightarrow x=49\)(tmđk)
b, đk x >= 0
\(\Leftrightarrow x< 2\)Kết hợp với đk vậy 0 =< x < 2
c, đk x >= 0 \(\Leftrightarrow2x< 16\Leftrightarrow x< 8\)
Kết hợp đk vậy 0 =< x < 8
a) \(2\sqrt{x}=14\)
Vì \(x\ge0\) nên bình phương hai vế ta được :
\(x=7^2\Leftrightarrow x=49\)
Vậy \(x=49\)
b) \(\sqrt{x}< \sqrt{2}\Leftrightarrow(\sqrt{x})^2< (\sqrt{2})^2\Leftrightarrow x< 4\)
c) \(\sqrt{2x}< 4\Leftrightarrow(\sqrt{2x})^2< 4^2\Leftrightarrow2x< 16\Leftrightarrow x< 8\)

\(\sqrt{\dfrac{2}{5}}\) + \(\sqrt{\dfrac{5}{2}}\) = \(\dfrac{\sqrt{2}\times\sqrt{2}}{\sqrt{10}}\)+ \(\dfrac{\sqrt{5}\times\sqrt{5}}{\sqrt{10}}\) = \(\dfrac{7}{\sqrt{10}}\)= \(\dfrac{7\sqrt{10}}{10}\)
Lời giải:
\(\sqrt{\frac{2}{5}}+\sqrt{\frac{5}{2}}=\frac{\sqrt{2}.\sqrt{2}+\sqrt{5}.\sqrt{5}}{\sqrt{5}.\sqrt{2}}=\frac{7}{\sqrt{10}}=\frac{7\sqrt{10}}{10}\)

a) \((2+\sqrt{3})\sqrt{7-4\sqrt{3}}\)
\(=(2+\sqrt{3})\sqrt{4-4\sqrt{3}+3}\)
\(=(2+\sqrt{3})\sqrt{(2-\sqrt{3})^2}\)
\(=(2+\sqrt{3})(2-\sqrt{3})=4-3=1\)
b) \(\sqrt{(1-\sqrt{2023})^2}\cdot\sqrt{2024+2\sqrt{2023}}\)
\(=|1-\sqrt{2023}|\sqrt{2023+2\sqrt{2023}+1}\)
\(=(\sqrt{2023}-1)\sqrt{(\sqrt{2023}+1)^2}\)
\(=(\sqrt{2023}-1)(\sqrt{2023}+1)\)
\(=\sqrt{2023^2}-1^2=2023-1=2022\)

`1/2(\sqrt{6}+\sqrt{5})^2-1/4\sqrt{120}-\sqrt{15}/2`
`=1/2 .(6+5+2\sqrt{30})-1/4 \sqrt{2^2 .30}-\sqrt{15}/2`
`=11/2+\sqrt{30}-1/2 \sqrt{30}-\sqrt{15}/2`
`=[11+2\sqrt{30}-\sqrt{30}-\sqrt{15}]/2`
`=[11+\sqrt{30}-\sqrt{15}]/2`
Lời giải:
$\frac{1}{2}(\sqrt{6}+\sqrt{5})^2-\frac{1}{4}\sqrt{120}-\frac{\sqrt{15}}{2}$
$=\frac{1}{2}(11+2\sqrt{30})-\frac{1}{2}\sqrt{30}-\frac{\sqrt{15}}{2}$
$=\frac{11}{2}+\frac{\sqrt{30}}{2}-\frac{\sqrt{15}}{2}$

a, △ABC vuông tại A có AH là đường cao.
\(\Rightarrow\left\{{}\begin{matrix}HB.BC=AB^2\\HC.BC=AC^2\end{matrix}\right.\) (hệ thức lượng trong tam giác vuông)
\(\Rightarrow\dfrac{HB.BC}{HC.BC}=\dfrac{HB}{HC}=\dfrac{AB^2}{AC^2}\)
b, △ABH vuông tại H có HD là đường cao.
\(\Rightarrow BD.AB=BH^2\) (hệ thức lượng trong tam giác vuông)
\(\Rightarrow BD=\dfrac{BH^2}{AB}\left(1\right)\)
△ACH vuông tại H có HE là đường cao.
\(\Rightarrow EC.AC=CH^2\) (hệ thức lượng trong tam giác vuông)
\(\Rightarrow EC=\dfrac{CH^2}{AC} \left(2\right)\)
Từ (1), (2) suy ra:
\(\dfrac{DB}{EC}=\dfrac{\dfrac{BH^2}{AB}}{\dfrac{CH^2}{AC}}=\left(\dfrac{BH}{CH}\right)^2.\dfrac{AC}{AB}=\dfrac{AB^4}{AC^4}.\dfrac{AC}{AB}=\left(\dfrac{AB}{AC}\right)^3\)
c, Có: \(\left\{{}\begin{matrix}BD.AB=BH^2\\EC.AC=CH^2\end{matrix}\right.\Rightarrow BD.EC.AB.AC=BH^2.CH^2\)
Mà \(\left\{{}\begin{matrix}BH.CH=AH^2\\AH.BC=AB.AC\end{matrix}\right.\)
\(\Rightarrow BD.EC.AH.BC=AH^4\)
\(\Rightarrow BD.EC.BC=AH^3\)
You yourself draw the figure.
a) Consider the right triangle ABC (which has \(\widehat{A}=90^o\)) has the height AH, thus, we have \(AB^2=HB.BC\)
Similarly, we have \(AC^2=HC.BC\)
From these, we get \(\dfrac{HB.BC}{HC.BC}=\dfrac{AB^2}{AC^2}\Leftrightarrow\dfrac{HB}{HC}=\left(\dfrac{AB}{AC}\right)^2\)
b) We can easily prove that \(\Delta BDH~\Delta HEC\left(a.a\right)\), therefore, \(\dfrac{DB}{HE}=\dfrac{HB}{HC}\)
Then, we can see that \(\dfrac{HB}{HC}=\left(\dfrac{AB}{AC}\right)^2\), so, we have \(\dfrac{DB}{HE}=\left(\dfrac{AB}{AC}\right)^2\), and the thing we have to prove is the same of \(\dfrac{DB}{HE}=\dfrac{DB}{EC}\) or \(HE=EC\), but this is clearly wrong. You have to edit the title.
c) This title is also wrong. \(BD.CE.BC=DB^3\Leftrightarrow CE.BC=DB^2\) which make no sense.

a, Với x khác 1 ; x khác 2/3
\(C=\left(\dfrac{2x}{2x^2-5x+3}-\dfrac{5}{2x-3}\right):\left(3+\dfrac{2}{1-x}\right)\)
\(=\left(\dfrac{2x-5x+5}{\left(2x-3\right)\left(x-1\right)}\right):\left(\dfrac{3-3x+2}{1-x}\right)=\dfrac{\left(5-3x\right)\left(1-x\right)}{\left(2x-3\right)\left(x-1\right)\left(5-3x\right)}=\dfrac{1}{3-2x}\)
b, Ta có |2x-3| + 1 = 8 <=> | 2x - 3 | = 7
TH1 : 2x - 3 = 7 <=> x = 5
TH2 : 2x - 3 = -7 <=> x = -2
Thay x = 5 vào ta được \(\dfrac{1}{3-2.5}=-\dfrac{1}{7}\)
Thay x = -2 vào ta được \(\dfrac{1}{3-2\left(-2\right)}=\dfrac{1}{7}\)
c, Ta có \(\dfrac{1}{3-2x}>0\Rightarrow3-2x>0\Leftrightarrow x< \dfrac{3}{2}\)
d, 3 - 2x thuộc Ư(1) = {-1;1}
| 3-2x | 1 | -1 |
| x | 1 | 2 |
e, \(\dfrac{1}{3-2x}=\dfrac{1}{6-x^2}\Leftrightarrow x^2-2x-3=0\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-3\end{matrix}\right.\)

\(A=\left(\dfrac{\sqrt{x}-1}{x-1}+\dfrac{2-2\sqrt{x}}{x\sqrt{x}+x-\sqrt{x}-1}\right)\div\left(\dfrac{\sqrt{x}+2}{x+\sqrt{x}-2}-\dfrac{2}{x-1}\right)\)
\(=\left(\dfrac{1}{\sqrt{x}+1}-\dfrac{2}{\left(\sqrt{x}+1\right)^2}\right)\div\left(\dfrac{1}{\sqrt{x}-1}-\dfrac{2}{x-1}\right)\)
\(=\dfrac{\sqrt{x}-1}{\left(\sqrt{x}+1\right)^2}\div\dfrac{\sqrt{x}-1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{\sqrt{x}-1}{\sqrt{x}+1}\)