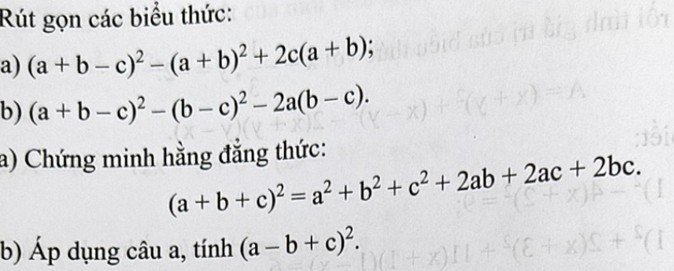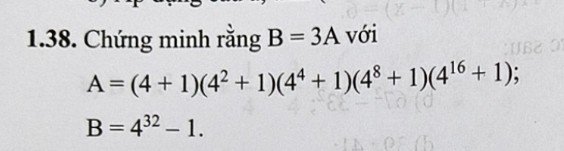phân tích x3-x2+5x-4 thành nhân tử
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: \(101^2=\left(100+1\right)^2=100^2+2\cdot100\cdot1+1^2\)
=10000+200+1
=10201
b: \(64^2+36^2+72\cdot64\)
\(=64^2+2\cdot64\cdot36+36^2\)
\(=\left(64+36\right)^2=100^2=10000\)
c: \(54^2+46^2-2\cdot54\cdot46=\left(54-46\right)^2=8^2=64\)
d: \(98\cdot102=\left(100-2\right)\left(100+2\right)=100^2-4=9996\)


`a) 2024x - 2024y - 2024x^2 + 4048xy - 2024y^2`
`= ( 2024x - 2024y) - (2024x^2 - 4048xy + 2024y^2)`
`= 2024 (x-y) - 2024 (x^2 - 2xy + y^2)`
`= 2024 (x-y) - 2024 (x-y)^2`
`= 2024 (x-y) (1 - x + y)`
`b) x^2 + 5x - 6`
`= (x^2 - x) + (6x - 6)`
`= x(x-1) + 6(x-1)`
`= (x+6)(x-1)`
`c) 2x^2 + 3x - 5`
`= (2x^2 - 2x) + (5x - 5)`
`= 2x(x - 1) + 5(x-1)`
`= (2x+5)(x-1)`
`d) x^4 + 4 `
`= (x^2)^2 + 2^2`
`= (x^2)^2 + 4x^2 + 2^2 - 4x^2`
`= (x^2 + 2)^2 - (2x)^2 `
`= (x^2 - 2x + 2)(x^2 + 2x+ 2)`
`e) x^5 + x + 1`
`= (x^5 - x^2) + (x^2 + x + 1)`
`= x^2 (x^3 - 1) + (x^2 + x + 1)`
`= x^2 (x-1) (x^2 + x + 1) + (x^2 + x + 1)`
`= (x^3 - x^2 + 1) (x^2 + x + 1) `

a) Ta có:
\(\left(a+b+c\right)^2\\ =\left[a+\left(b+c\right)\right]^2\\ =a^2+2a\left(b+c\right)+\left(b+c\right)^2\\ =a^2+2ab+2ac+b^2+2bc+c^2\\ =a^2+b^2+c^2+2ab+2ac+2bc\)
=> Đpcm
b)
\(\left(a-b+c\right)^2\\ =\left[a+\left(-b\right)+c\right]^2\\ =a^2+\left(-b\right)^2+c^2+2a\left(-b\right)+2ac+2\left(-b\right)c\\ =a^2+b^2+c^2-2ab+2ac-2bc\)

\(\dfrac{3001}{5002}=1-\dfrac{2001}{5002}< 1\)
\(\dfrac{444111}{666111}=\dfrac{4001\times111}{6001\times111}=\dfrac{4001}{6001}=1-\dfrac{2000}{6001}< 1\)
\(\dfrac{30303040404}{505050}>1\)
Ta có: \(\dfrac{2001}{5002}>\dfrac{2000}{5002}>\dfrac{2000}{6001}\)
=> \(1-\dfrac{2001}{5002}< 1-\dfrac{2000}{6001}\)
=> \(\dfrac{3001}{5002}< \dfrac{444111}{666111}\)
Vậy:
Thứ tự sắp xếp từ bé đến lớn là:
\(\dfrac{3001}{5002};\dfrac{444111}{666111};\dfrac{30303040404}{505050}\)
Thứ tự sắp xếp từ lớn đến bé là:
\(\dfrac{30303040404}{505050};\dfrac{444111}{666111};\dfrac{3001}{5002}\)

\(B=4^{31}-1\\ =\left(4^{16}-1\right)\left(4^{16}+1\right)\\ =\left(4^8-1\right)\left(4^8+1\right)\left(4^{16}+1\right)\\ =\left(4^4-1\right)\left(4^4+1\right)\left(4^8+1\right)\left(4^{16}+1\right)\\ =\left(4^2-1\right)\left(4^2+1\right)\left(4^4+1\right)\left(4^8+1\right)\left(4^{16}+1\right)\\ =\left(4-1\right)\left(4+1\right)\left(4^2+1\right)\left(4^4+1\right)\left(4^8+1\right)\left(4^{16}+1\right)\\ =3\left[\left(4+1\right)\left(4^2+1\right)\left(4^4+1\right)\left(4^8+1\right)\left(4^{16}+1\right)\right]\\ =3A\)