Ai giải giúp mình bài này với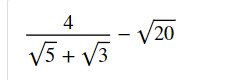
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\sqrt{5+2\sqrt{6}}-\sqrt{5-2\sqrt{6}}\\ =\sqrt{\left(\sqrt{3}\right)^2+2\cdot\sqrt{3}\cdot\sqrt{2}+\left(\sqrt{2}\right)^2}-\sqrt{\left(\sqrt{3}\right)^2-2\cdot\sqrt{3}\cdot\sqrt{2}+\left(\sqrt{2}\right)^2}\\ =\sqrt{\left(\sqrt{3}+\sqrt{2}\right)^2}-\sqrt{\left(\sqrt{3}-\sqrt{2}\right)^2}\\ =\sqrt{3}+\sqrt{2}-\sqrt{3}+\sqrt{2}\\ =2\sqrt{2}\)

Bài 1:
a) Để căn thức có nghĩa thì:
\(x+1\ge0\Leftrightarrow x\ge-1\)
b) Để căn thức có nghĩa thì:
\(3x-8\ge0\Leftrightarrow3x\ge8\Leftrightarrow x\ge\dfrac{8}{3}\)
c) Để căn thức có nghĩa thì:
\(2x^2+3>0\)
Mà điều này luôn đúng nên căn thức có nghĩa khi x ∈ R
d) Để căn thức có nghĩa thì:
\(16-x^2\ge0\Leftrightarrow\left(4-x\right)\left(4+x\right)\ge0\Leftrightarrow-4\le x\le4\)
Câu 1: B
Câu 2: D
Câu 3: ĐKXĐ: 2x+5>=0
=>2x>=-5
=>\(x>=-\dfrac{5}{2}\)
=>Chọn C
Câu 4: ĐKXĐ: 3-4x>=0
=>-4x>=-3
=>4x<=3
=>\(x< =\dfrac{3}{4}\)
=>Chọn D
Câu 5: \(\sqrt{7}-\sqrt{\left(1-\sqrt{7}\right)^2}\)
\(=\sqrt{7}-\left|1-\sqrt{7}\right|\)
\(=\sqrt{7}-\sqrt{7}+1=1\)
=>Chọn B
Câu 6: \(\sqrt{x^2-6x+9}=\sqrt{\left(x-3\right)^2}=\left|x-3\right|\)
x>=3 nên x-3>=0
=>\(\sqrt{x^2-6x+9}=\left|x-3\right|=x-3\)
=>Chọn B
Câu 7: \(\sqrt{25+x^2+10x}=\sqrt{x^2+10x+25}=\sqrt{\left(x+5\right)^2}=\left|x+5\right|\)
x<-6
=>x+6<0
mà x+5<x+6
nên x+5<0
=>\(\sqrt{25+x^2+10x}=-\left(x+5\right)\)
=>Chọn D
Câu 8: \(M=2x-\sqrt{x^4+2x^2+1}\)
\(=2x-\sqrt{\left(x^2+1\right)^2}\)
\(=2x-\left(x^2+1\right)=-\left(x^2-2x+1\right)=-\left(x-1\right)^2\)
Thay x=11 vào M, ta được:
\(M=-\left(11-1\right)^2=-10^2=-100\)
=>Chọn A
Câu 9: \(\sqrt{x-7}=2\)
=>\(x-7=2^2=4\)
=>x=4+7=11
=>Chọn C
Câu 10: \(\sqrt{a^4b^2}=\sqrt{a^4}\cdot\sqrt{b^2}=a^2\cdot\left|b\right|\)
=>Chọn D
Câu 11: \(\dfrac{1}{2+\sqrt{3}}+\dfrac{1}{2-\sqrt{3}}\)
\(=\dfrac{2-\sqrt{3}+2+\sqrt{3}}{\left(2+\sqrt{3}\right)\left(2-\sqrt{3}\right)}\)
\(=\dfrac{4}{4-3}=4\)
=>Chọn C
Câu 12: A

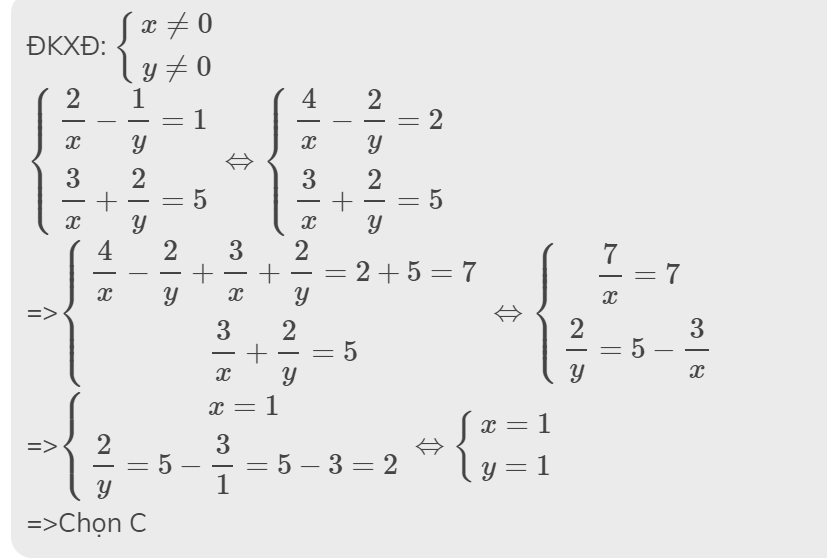
ĐKXĐ: \(\left\{{}\begin{matrix}x\ne0\\y\ne0\end{matrix}\right.\)
\(\left\{{}\begin{matrix}\dfrac{2}{x}-\dfrac{1}{y}=1\\\dfrac{3}{x}+\dfrac{2}{y}=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{4}{x}-\dfrac{2}{y}=2\\\dfrac{3}{x}+\dfrac{2}{y}=5\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{4}{x}-\dfrac{2}{y}+\dfrac{3}{x}+\dfrac{2}{y}=2+5=7\\\dfrac{3}{x}+\dfrac{2}{y}=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{7}{x}=7\\\dfrac{2}{y}=5-\dfrac{3}{x}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=1\\\dfrac{2}{y}=5-\dfrac{3}{1}=5-3=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=1\end{matrix}\right.\)
=>Chọn C

ĐKXĐ: \(\left\{{}\begin{matrix}x>=0\\y>=0\end{matrix}\right.\)
\(\left\{{}\begin{matrix}2\sqrt{x}+\sqrt{y}=5\\3\sqrt{x}-\sqrt{y}=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2\sqrt{x}+\sqrt{y}+3\sqrt{x}-\sqrt{y}=5+1\\2\sqrt{x}+\sqrt{y}=5\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}5\sqrt{x}=6\\\sqrt{y}=5-2\sqrt{x}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\sqrt{x}=\dfrac{6}{5}\\\sqrt{y}=5-2\cdot\dfrac{6}{5}=5-\dfrac{12}{5}=\dfrac{13}{5}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{36}{25}\\y=\dfrac{169}{25}\end{matrix}\right.\)
=>Chọn B
\(\left\{{}\begin{matrix}2\sqrt{x}+\sqrt{y}=5\\3\sqrt{x}-\sqrt{y}=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}5\sqrt{x}=6\\2\sqrt{x}+\sqrt{y}=5\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}\sqrt{x}=\dfrac{6}{5}\\\dfrac{12}{5}+\sqrt{y}=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{36}{25}\\\sqrt{y}=5-\dfrac{12}{5}=\dfrac{13}{5}\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{36}{25}\\y=\left(\dfrac{13}{5}\right)^2=\dfrac{169}{25}\end{matrix}\right.\)
=> Chọn B

\(1.\left\{{}\begin{matrix}-x+3y=-10\\x-5y=16\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-2y=6\\x-5y=16\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=\dfrac{6}{-2}=-3\\x-5\cdot\left(-3\right)=16\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}y=-3\\x+15=16\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=-3\\x=16-15=1\end{matrix}\right.\\ 2.\left\{{}\begin{matrix}2x+y=7\\-x+4y=10\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x+y=7\\-2x+8y=20\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x+y=7\\9x=27\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}2x+y=7\\x=\dfrac{27}{9}=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2\cdot3+y=7\\x=3\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}y=7-6=1\\x=3\end{matrix}\right.\)
\(3.\left\{{}\begin{matrix}3x-5y=-18\\x+2y=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3x-5y=-18\\3x+6y=15\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=-3\\x+2\cdot\left(-3\right)=5\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}y=-3\\x=5+6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=-3\\x=11\end{matrix}\right.\\ 4.\left\{{}\begin{matrix}4x+3y=-6\\2x-5y=16\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}4x+3y=-6\\4x-10y=32\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}13y=-38\\2x-5y=16\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}y=\dfrac{-38}{13}\\2x-5\cdot\dfrac{-38}{13}=16\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=\dfrac{-38}{13}\\2x+\dfrac{190}{13}=16\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}y=\dfrac{-38}{13}\\2x=16-\dfrac{190}{13}=\dfrac{18}{13}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=\dfrac{-38}{13}\\x=\dfrac{18}{13}:2=\dfrac{9}{13}\end{matrix}\right.\)
20: \(\left\{{}\begin{matrix}2x+y=5\\x+7y=9\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x+y=5\\2x+14y=18\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2x+14y-2x-y=18-5\\2x+y=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}13y=13\\2x=5-y\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=1\\2x=5-1=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=1\\x=2\end{matrix}\right.\)
21: \(\left\{{}\begin{matrix}5x+3y=-7\\3x-y=-8\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}5x+3y=-7\\9x-3y=-24\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}5x+3y+9x-3y=-7-24\\3x-y=-8\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}14x=-31\\y=3x+8\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=-\dfrac{31}{14}\\y=3\cdot\dfrac{-31}{14}+8=-\dfrac{93}{14}+\dfrac{112}{14}=\dfrac{19}{14}\end{matrix}\right.\)
22: \(\left\{{}\begin{matrix}-2x+y=-3\\3x+4y=10\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=-3+2x\\3x+4\left(2x-3\right)=10\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=2x-3\\3x+8x-12=10\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}11x=22\\y=2x-3\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=2\\y=2\cdot2-3=4-3=1\end{matrix}\right.\)
23: \(\left\{{}\begin{matrix}x+y=2\\x+3y=6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x+3y-x-y=6-2\\x+y=2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2y=4\\x+y=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=2\\x=2-y=2-2=0\end{matrix}\right.\)
24: \(\left\{{}\begin{matrix}x-2y=-5\\3x+4y=-5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x-4y=-10\\3x+4y=-5\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2x-4y+3x+4y=-10-5\\x-2y=-5\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}5x=-15\\2y=x+5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-3\\2y=-3+5=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-3\\y=1\end{matrix}\right.\)
25: \(\left\{{}\begin{matrix}3x-2y=12\\4x+y=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3x-2y=12\\8x+2y=10\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}3x-2y+8x+2y=12+10\\4x+y=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}11x=22\\y=5-4x\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=2\\y=5-4\cdot2=5-8=-3\end{matrix}\right.\)
26: \(\left\{{}\begin{matrix}2x-y=10\\5x+2y=6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}4x-2y=20\\5x+2y=6\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}4x-2y+5x+2y=20+6\\2x-y=10\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}9x=26\\y=2x-10\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{26}{9}\\y=2x-10=2\cdot\dfrac{26}{9}-10=\dfrac{52}{9}-10=-\dfrac{38}{9}\end{matrix}\right.\)
27: \(\left\{{}\begin{matrix}5x-2y=10\\5x-2y=6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}5x-2y-5x+2y=10-6\\5x-2y=6\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}0x=4\\2y=5x-6\end{matrix}\right.\Leftrightarrow\left(x;y\right)\in\varnothing\)
28: \(\left\{{}\begin{matrix}3x+2y=8\\4x-3y=-12\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}12x+8y=32\\12x-9y=-36\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}12x+8y-12x+9y=32+36\\3x+2y=8\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}17y=68\\3x=8-2y\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=4\\3x=8-2\cdot4=8-8=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=0\\y=4\end{matrix}\right.\)
37: \(\left\{{}\begin{matrix}2x+y=4\\2x+0y-6=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x=6\\y=4-2x=4-6=-2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=3\\y=-2\end{matrix}\right.\)
38: \(\left\{{}\begin{matrix}x-2y=2\\2x-4y=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x-4y=4\\2x-4y=1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2x-4y-2x+4y=4-1\\x-2y=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}0y=3\\x-2y=2\end{matrix}\right.\)
=>\(\left(x;y\right)\in\varnothing\)
39: \(\left\{{}\begin{matrix}3x+2y-2=0\\9x+6y-4=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3x+2y=2\\9x+6y=4\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}9x+6y=6\\9x+6y=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}0y=2\\3x+2y=2\end{matrix}\right.\Leftrightarrow\left(x;y\right)\in\varnothing\)
40: \(\left\{{}\begin{matrix}2x-y=2\\4x-2y-4=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x-y=2\\4x-2y=4\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2x-y=2\\2x-y=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}0x=0\\y=2x-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\in R\\y=2x-2\end{matrix}\right.\)
41: \(\left\{{}\begin{matrix}x+2y=4\\2x+9y=18\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x+4y=8\\2x+9y=18\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2x+9y-2x-4y=18-8\\x+2y=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}5y=10\\x=4-2y\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=2\\x=4-2\cdot2=4-4=0\end{matrix}\right.\)
42: \(\left\{{}\begin{matrix}-2x+y=-3\\x+y=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-2x+y-x-y=-3-3\\x+y=3\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}-3x=-6\\y=3-x\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=3-2=1\end{matrix}\right.\)
43: \(\left\{{}\begin{matrix}x-y=0\\2x+y=-5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x-y+2x+y=0-5\\x=y\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}3x=-5\\y=x\end{matrix}\right.\Leftrightarrow y=x=-\dfrac{5}{3}\)
44: \(\left\{{}\begin{matrix}2x+y=0\\x-4y=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=-2x\\x-4\cdot\left(-2x\right)=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}9x=0\\y=-2x\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=-2\cdot0=0\end{matrix}\right.\)
45: \(\left\{{}\begin{matrix}-x+y=3\\x+2y=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-x+y+x+2y=3+3\\x+2y=3\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}3y=6\\x=3-2y\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=2\\x=3-2\cdot2=3-4=-1\end{matrix}\right.\)
46: \(\left\{{}\begin{matrix}x-y=2\\3x-2y=9\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3x-3y=6\\3x-2y=9\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}3x-3y-2x+2y=6-9\\x-y=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-y=-3\\x=y+2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=3\\x=3+2=5\end{matrix}\right.\)

\(\left\{{}\begin{matrix}3x-4y=-2\\5x+2y=14\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3x-4y=-2\\2y=14-5x\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}3x-2\cdot2y=-2\\2y=14-5x\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3x-2\left(14-5x\right)=-2\\2y=14-5x\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}3x-28+10x=-2\\2y=-5x+14\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}13x=-2+28=26\\2y=-5x+14\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=2\\2y=-5\cdot2+14=14-10=4\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=2\\y=2\end{matrix}\right.\)

\(6)\left(2x+1\right)^2-\left(x+3\right)^2=0\\ \Leftrightarrow\left(2x+1-x-3\right)\left(2x+1+x+3\right)=0\\ \Leftrightarrow\left(x-2\right)\left(3x+4\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x-2=0\\3x+4=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=2\\x=-\dfrac{4}{3}\end{matrix}\right.\\ 7)\left(x^2-4\right)+x\left(x-2\right)=0\\ \Leftrightarrow\left(x-2\right)\left(x+2\right)+x\left(x-2\right)=0\\ \Leftrightarrow\left(x-2\right)\left(x+2+x\right)=0\\ \Leftrightarrow\left(x-2\right)\left(2x+2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x-2=0\\2x+2=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=2\\x=-1\end{matrix}\right.\\ 8)2\left(x+1\right)=\left(5x-1\right)\left(x+1\right)\\ \Leftrightarrow2\left(x+1\right)-\left(5x-1\right)\left(x+1\right)=0\\ \Leftrightarrow\left(x+1\right)\left(2-5x+1\right)=0\\ \Leftrightarrow\left(x+1\right)\left(3-5x\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=-1\\x=\dfrac{3}{5}\end{matrix}\right.\\ 9)\left(-4x+3\right)x=\left(2x+5\right)x\\ \Leftrightarrow\left(-4x+3\right)x-\left(2x+5\right)x=0\\ \Leftrightarrow x\left(-4x+3-2x-5\right)=0\\ \Leftrightarrow x\left(-6x-2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x=-\dfrac{1}{3}\end{matrix}\right.\)

a: Ta có: ΔOCK vuông tại C
=>\(CK^2+CO^2=OK^2\)
=>\(CK=\sqrt{10^2-8^2}=6\left(cm\right)\)
Xét ΔOCK vuông tại C có CA là đường cao
nên \(OA\cdot OK=OC^2;CA\cdot OK=CO\cdot CK\)
=>\(OA=\dfrac{OC^2}{OK}=\dfrac{8^2}{10}=6,4\left(cm\right);CA=\dfrac{6\cdot8}{10}=4,8\left(cm\right)\)
Xét ΔCOK vuông tại C có \(sinCOK=\dfrac{CK}{OK}=\dfrac{6}{10}=\dfrac{3}{5}\)
nên \(\widehat{COK}=\widehat{xOy}\simeq36^052'\)
b: Xét ΔCAO vuông tại A có AH là đường cao
nên \(CH\cdot CO=CA^2\left(1\right)\)
Xét ΔCOK vuông tại O có CA là đường cao
nên \(AO\cdot AK=AC^2\left(2\right)\)
Từ (1),(2) suy ra \(CH\cdot CO=AO\cdot AK\)
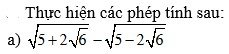

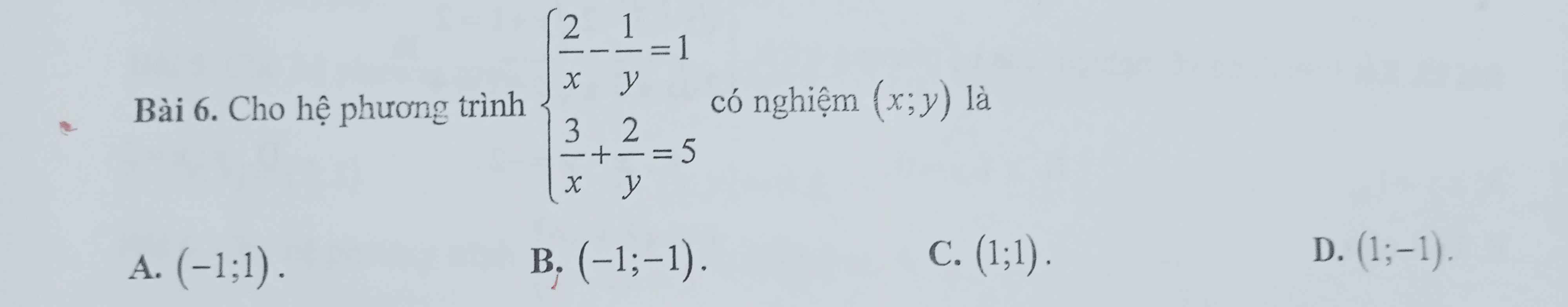
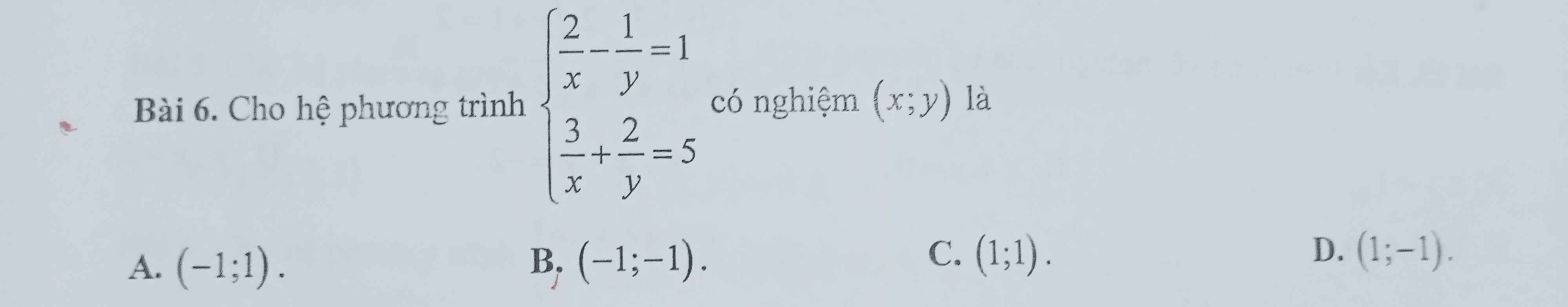
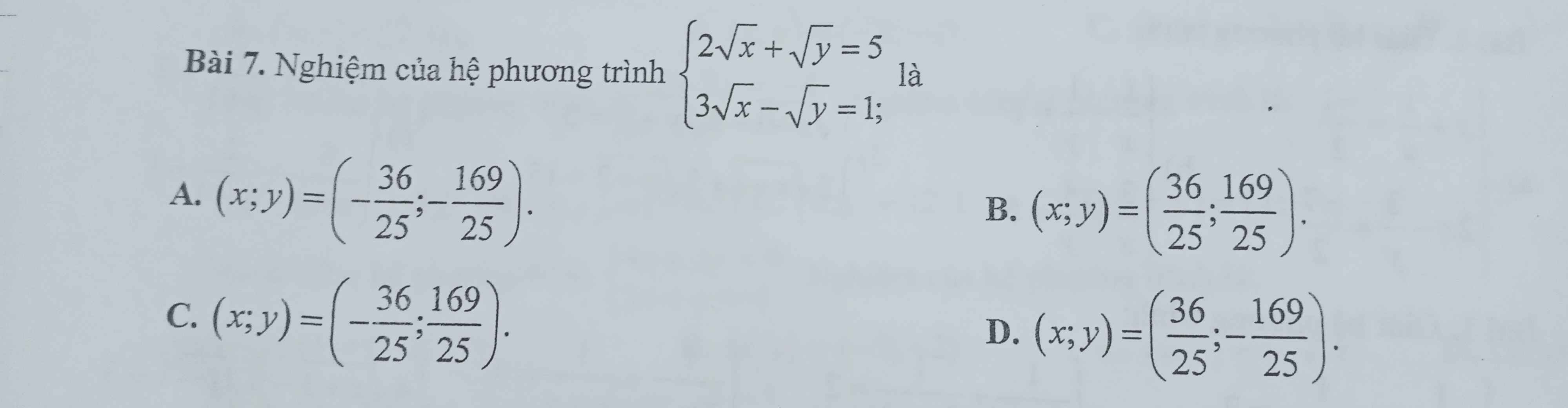
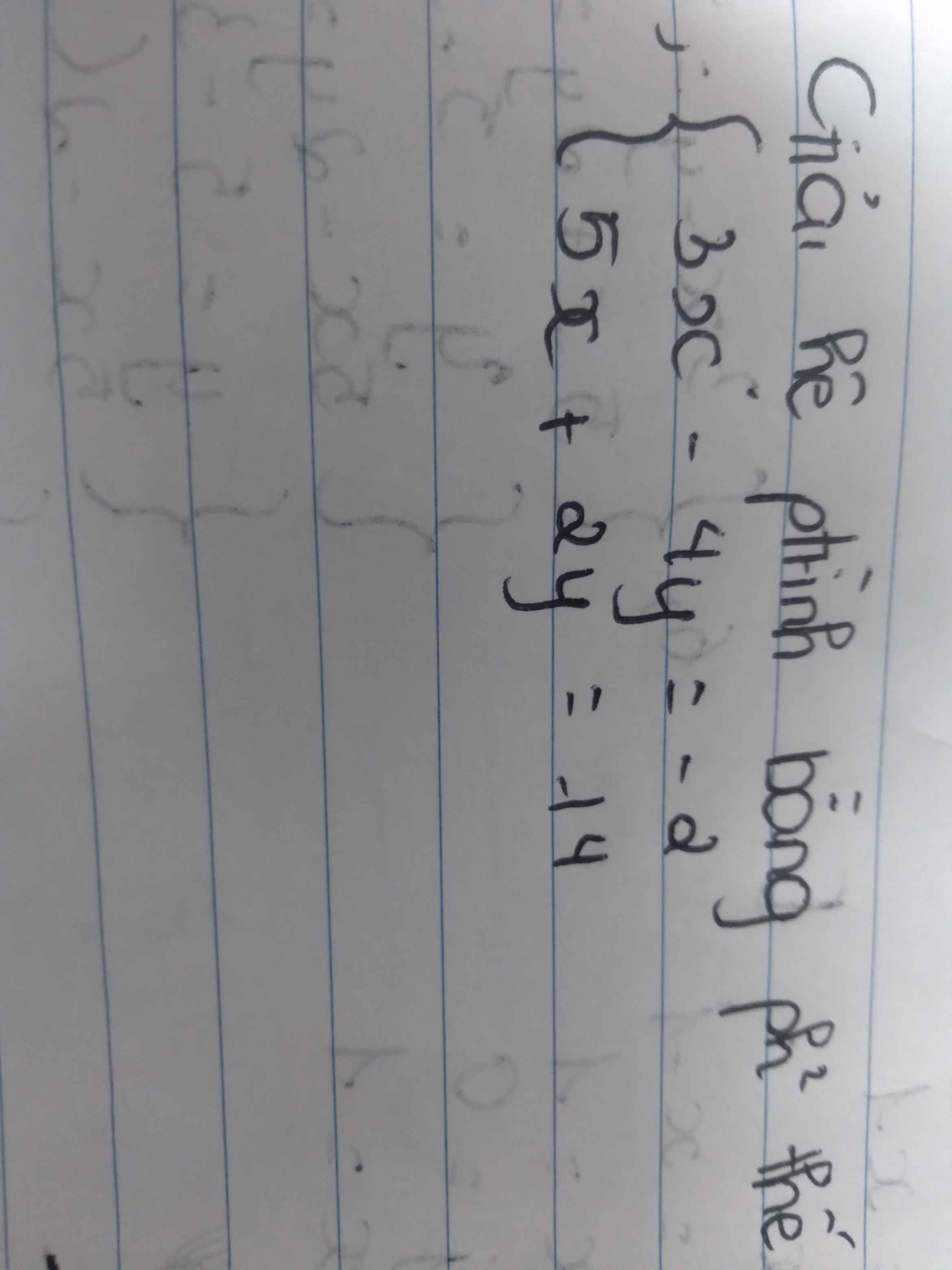
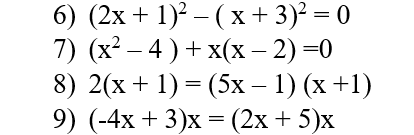

\(\dfrac{4}{\sqrt{5}+\sqrt{3}}-\sqrt{20}\\ =\dfrac{4\left(\sqrt{5}-\sqrt{3}\right)}{\left(\sqrt{5}+\sqrt{3}\right)\left(\sqrt{5}-\sqrt{3}\right)}-\sqrt{20}\\ =\dfrac{4\left(\sqrt{5}-\sqrt{3}\right)}{\left(\sqrt{5}\right)^2-\left(\sqrt{3}\right)^2}-\sqrt{2^2\cdot5}\\ =\dfrac{4\left(\sqrt{5}-\sqrt{3}\right)}{5-3}-2\sqrt{5}\\ =\dfrac{4\left(\sqrt{5}-\sqrt{3}\right)}{2}-2\sqrt{5}\\ =2\left(\sqrt{5}-\sqrt{3}\right)-2\sqrt{5}\\ =2\sqrt{5}-2\sqrt{3}-2\sqrt{5}\\ =-2\sqrt{3}\)