 giúp mình nhé cảm ơn :((
giúp mình nhé cảm ơn :((
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Thể tích nước buổi sáng bơm vào là:
\(2\cdot1,6\cdot1,5\cdot80\%=3,2\cdot1,2=3,84\left(m^3\right)=3840\left(lít\right)\)
Lượng nước còn lại sau khi dùng là:
\(3840\left(1-80\%\right)=768\left(lít\right)\)
2m=20dm; 1,6m=16dm; 1,5m=15dm
Thể tích tối đa của bể là: \(20\cdot16\cdot15=300\cdot16=4800\left(lít\right)\)
Lượng nước cần bơm vào là:
4800-768=4032(lít)

Đề sai rồi á bạn, mình nghĩ là phải chia hết cho 120 hoặc 100 chứ biểu thức đó k chia hết cho 105 đâu

a: Oz là phân giác của góc xOy
=>\(\widehat{xOz}=\widehat{yOz}=\dfrac{\widehat{xOy}}{2}=\dfrac{80^0}{2}=40^0\)

\(\left(\dfrac{-4}{5}+\dfrac{-3}{2}:x\right)\cdot\dfrac{1}{3}-\dfrac{1}{2}=\dfrac{1}{2}\\ \left(\dfrac{-4}{5}+\dfrac{-3}{2}:x\right)\cdot\dfrac{1}{3}=\dfrac{1}{2}+\dfrac{1}{2}\\ \left(\dfrac{-4}{5}+\dfrac{-3}{2}\right):x\cdot\dfrac{1}{3}=1\\ \dfrac{-4}{5}+\dfrac{-3}{2}:x=1:\dfrac{1}{3}\\ -\dfrac{4}{5}+\dfrac{-3}{2}x=3\\ \dfrac{3}{2}x=\dfrac{-4}{5}-3\\ \dfrac{3}{2}x=-\dfrac{19}{5}\\ x=\dfrac{-19}{5}:\dfrac{3}{2}\\x =-\dfrac{38}{15}\)

1) Ta có:
∠xOn + ∠mOn = 180⁰ (kề bù)
⇒ ∠xOn = 180⁰ - ∠mOn
= 180⁰ - 130⁰
= 50⁰
2) Ta có:
∠xOt + ∠xOn = 180⁰ (kề bù)
⇒ ∠xOt = 180⁰ - ∠xOn
= 180⁰ - 60⁰
= 120⁰
∠tOm = ∠xOn = 60⁰ (đối đỉnh)
∠mOn = ∠xOt = 120⁰ (đối đỉnh)

Gọi số học sinh lớp 7A,7B,7C lần lượt là a(bạn),b(bạn),c(bạn)
(Điều kiện: \(a,b,c\in Z^+\))
Số học sinh của lớp 7C lớn hơn số học sinh của lớp 7A là 3 bạn nên c-a=3
Tỉ số giữa số học sinh lớp 7A và 7B là 16:15
=>\(\dfrac{a}{16}=\dfrac{b}{15}\)
=>\(\dfrac{a}{32}=\dfrac{b}{30}\)
Tỉ số giữa số học sinh lớp 7B và 7C là 6:7
=>\(\dfrac{b}{6}=\dfrac{c}{7}\)
=>\(\dfrac{b}{30}=\dfrac{c}{35}\)
Do đó: \(\dfrac{a}{32}=\dfrac{b}{30}=\dfrac{c}{35}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{32}=\dfrac{b}{30}=\dfrac{c}{35}=\dfrac{c-a}{35-32}=1\)
=>a=32;b=30;c=35
Vậy: số học sinh lớp 7A,7B,7C lần lượt là 32(bạn), 30(bạn), 35(bạn)

Bài 1: \(\widehat{xOn}+\widehat{mOn}=180^0\)(hai góc kề bù)
=>\(\widehat{xOn}+30^0=180^0\)
=>\(\widehat{xOn}=150^0\)
Bài 2:
Ta có: \(\widehat{xOt}+\widehat{xOn}=180^0\)(hai góc kề bù)
=>\(\widehat{xOt}=180^0-60^0=120^0\)
Ta có: \(\widehat{xOn}=\widehat{tOm}\)(hai góc đối đỉnh)
mà \(\widehat{xOn}=60^0\)
nên \(\widehat{tOm}=60^0\)
Ta có: \(\widehat{xOt}=\widehat{mOn}\)(hai góc đối đỉnh)
mà \(\widehat{xOt}=120^0\)
nên \(\widehat{mOn}=120^0\)

\(\dfrac{0,4-\dfrac{2}{9}+\dfrac{2}{11}}{1,4-\dfrac{7}{9}+\dfrac{7}{11}}-\dfrac{\dfrac{1}{3}-0,25+\dfrac{1}{7}}{1\dfrac{1}{6}-0,875+\dfrac{1}{2}}\)
= \(\dfrac{\dfrac{2}{5}-\dfrac{2}{9}+\dfrac{2}{11}}{\dfrac{7}{5}-\dfrac{7}{9}+\dfrac{7}{11}}-\dfrac{\dfrac{2}{6}-\dfrac{2}{8}+\dfrac{2}{14}}{\dfrac{7}{6}-\dfrac{7}{8}+\dfrac{7}{14}}\)
= \(\dfrac{2.\left(\dfrac{1}{5}-\dfrac{1}{9}+\dfrac{1}{11}\right)}{7.\left(\dfrac{1}{5}-\dfrac{1}{9}+\dfrac{1}{11}\right)}-\dfrac{2.\left(\dfrac{1}{6}-\dfrac{1}{8}+\dfrac{1}{14}\right)}{7.\left(\dfrac{1}{6}-\dfrac{1}{8}+\dfrac{1}{14}\right)}\)
= \(\dfrac{2}{7}-\dfrac{2}{7}\)
= `0`
\(=\dfrac{2.\left(0,2-\dfrac{1}{7}+\dfrac{1}{11}\right)}{7.\left(0,2-\dfrac{1}{7}+\dfrac{1}{11}\right)}-\dfrac{2.\left(\dfrac{1}{6}-0,125+\dfrac{1}{14}\right)}{7.\left(\dfrac{1}{6}-0,125+\dfrac{1}{14}\right)}\)
\(=\dfrac{2}{7}-\dfrac{2}{7}=0\)

a: \(\left|5-\dfrac{2}{3}x\right|>=0\forall x;\left|\dfrac{2}{3}y-4\right|>=0\forall y\)
Do đó: \(\left|5-\dfrac{2}{3}x\right|+\left|\dfrac{2}{3}y-4\right|>=0\forall x,y\)
Dấu '=' xảy ra khi \(\left\{{}\begin{matrix}5-\dfrac{2}{3}x=0\\\dfrac{2}{3}y-4=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=5:\dfrac{2}{3}=\dfrac{15}{2}\\y=4:\dfrac{2}{3}=6\end{matrix}\right.\)
b: \(\left|\dfrac{2}{3}-\dfrac{1}{2}+\dfrac{3}{4}x\right|>=0\forall x;\left|1,5-\dfrac{3}{4}-\dfrac{3}{2}y\right|>=0\forall y\)
Do đó: \(\left\{{}\begin{matrix}\dfrac{2}{3}-\dfrac{1}{2}+\dfrac{3}{4}x=0\\1,5-\dfrac{3}{4}-\dfrac{3}{2}y=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{3}{4}x=-\dfrac{2}{3}+\dfrac{1}{2}=-\dfrac{1}{6}\\\dfrac{3}{2}y=1,5-\dfrac{3}{4}=\dfrac{3}{2}-\dfrac{3}{4}=\dfrac{3}{4}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=-\dfrac{1}{6}:\dfrac{3}{4}=-\dfrac{1}{6}\cdot\dfrac{4}{3}=\dfrac{-4}{18}=-\dfrac{2}{9}\\y=\dfrac{1}{2}\end{matrix}\right.\)
c: \(\left|x-2020\right|>=0\forall x;\left|y-2021\right|>=0\forall y\)
Do đó: \(\left|x-2020\right|+\left|y-2021\right|>=0\forall x,y\)
Dấu '=' xảy ra khi \(\left\{{}\begin{matrix}x-2020=0\\y-2021=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2020\\y=2021\end{matrix}\right.\)
d: \(\left|x-y\right|>=0\forall x,y\)
\(\left|y+\dfrac{21}{10}\right|>=0\forall y\)
Do đó: \(\left|x-y\right|+\left|y+\dfrac{21}{10}\right|>=0\forall x,y\)
Dấu '=' xảy ra khi \(\left\{{}\begin{matrix}x-y=0\\y+\dfrac{21}{10}=0\end{matrix}\right.\Leftrightarrow x=y=-\dfrac{21}{10}\)
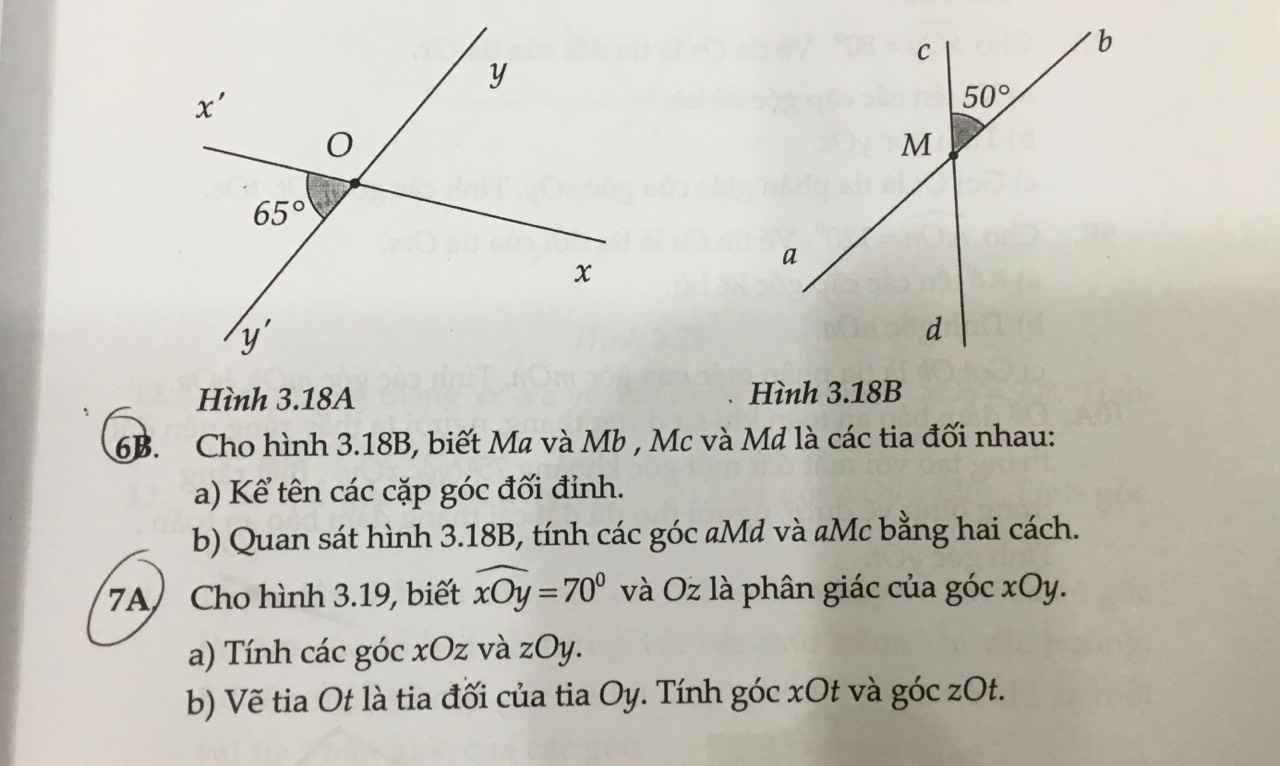
6B:
a: Các cặp góc đối đỉnh là: \(\widehat{cMb};\widehat{aMd}\); \(\widehat{aMc};\widehat{bMd}\)
b:
Cách 1: \(\widehat{aMc}+\widehat{cMb}=180^0\)(hai góc kề bù)
=>\(\widehat{aMc}=180^0-50^0=130^0\)
Ta có: \(\widehat{aMc}+\widehat{aMd}=180^0\)(hai góc kề bù)
=>\(\widehat{aMd}=180^0-130^0=50^0\)
Cách 2:
Ta có: \(\widehat{aMd}=\widehat{cMb}\)(hai góc đối đỉnh)
mà \(\widehat{cMb}=50^0\)
nên \(\widehat{aMd}=50^0\)
Ta có: \(\widehat{aMd}+\widehat{aMc}=180^0\)(hai góc kề bù)
=>\(\widehat{aMc}+50^0=180^0\)
=>\(\widehat{aMc}=130^0\)
7A:
a: Oz là phân giác của góc xOy
=>\(\widehat{xOz}=\widehat{zOy}=\dfrac{\widehat{xOy}}{2}=35^0\)
b: Ta có: \(\widehat{xOy}+\widehat{xOt}=180^0\)(hai góc kề bù)
=>\(\widehat{xOt}+70^0=180^0\)
=>\(\widehat{xOt}=110^0\)
Ta có: \(\widehat{zOt}+\widehat{zOy}=180^0\)(hai góc kề bù)
=>\(\widehat{zOt}+35^0=180^0\)
=>\(\widehat{zOt}=145^0\)