Cho đường tròn (O; 5cm) và điểm O' với OO' = 7cm. Vẽ đường tròn (O';R'). Với giá trị nào của R' thì đường tròn (O'; R')
a, Cắt đường tròn (O)
b, Tiếp xúc với đường tròn (O).
c. Không có điểm chung vs (O)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
NA
12 tháng 11 2022
z,\:x^3+y^3+x\cdot \:3=3xyz\quad :\quad z=\frac{x^3+y^3+3x}{3xy};\quad \:x\ne \:0
x^3+y^3+x\cdot \:3=3xyz
\frac{3xyz}{3xy}=\frac{x^3}{3xy}+\frac{y^3}{3xy}+\frac{x\cdot \:3}{3xy};\quad \:x\ne \:0
z=\frac{x^3+y^3+3x}{3xy};\quad \:x\ne \:0
12 tháng 11 2022
d1 cắt d2 khi a≠a', b=b' ĐK: 4-m≠0⇒m≠4 m-2≠0⇒m≠2
⇔2x≠3x và 4-m = m-2 ⇒ -2m = -6 ⇒ m = 3 (thoả mãn đk)
tính đến đây thì bn thử cho x=1=>y sau đó vẽ trục toạ độ sẽ thấy d1 ko cắt d2 trên trục tung
NV
Nguyễn Việt Lâm
Giáo viên
11 tháng 11 2022
\(Q=\sqrt[3]{\left(2x\sqrt[]{2x}+1\right)\left(2x\sqrt[]{2x}-1\right)}+\sqrt[3]{8x^3-1}\)
\(=\sqrt[3]{8x^3-1}+\sqrt[3]{8x^3-1}\)
\(=2\sqrt[3]{8x^3-1}\)
NV
Nguyễn Việt Lâm
Giáo viên
10 tháng 11 2022
BĐT cần chứng minh tương đương:
\(2a+2b+2\ge2\sqrt{a}+2\sqrt{b}+2\sqrt{ab}\)
\(\Leftrightarrow\left(a-2\sqrt{a}+1\right)+\left(b-2\sqrt{b}+1\right)+\left(a+b-2\sqrt{ab}\right)\ge0\)
\(\Leftrightarrow\left(\sqrt{a}-1\right)^2+\left(\sqrt{b}-1\right)^2+\left(\sqrt{a}-\sqrt{b}\right)^2\ge0\) (luôn đúng với a;b không âm)
Vậy BĐT đã cho được chứng minh
Dấu "=" xảy ra khi và chỉ khi \(a=b=1\)
11 tháng 11 2022
Áp dụng bđt côsi với các số không âm ta có:
\(a+b\ge2\sqrt{ab}\\ a+1\ge2\sqrt{a}\\ b+1\ge2\sqrt{b}\)
=> \(a+b+a+1+b+1\ge2\sqrt{ab}+2\sqrt{a}+2\sqrt{b}\)
=> \(2a+2b+2\ge2\sqrt{ab}+2\sqrt{a}+2\sqrt{b}\)
=> \(a+b+1\ge\sqrt{a}+\sqrt{b}+\sqrt{ab}\) ( ĐPCM)
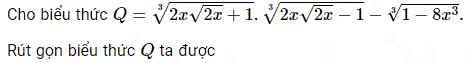
a, R' ≥ 2 ≤ 6
b, R' = 2 cm
c, R' = 1 cm
Mong giúp ích cho bn !